- 2021-04-28 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学中考复习课件章节考点专题突破:第五章 图形性质1-20 三角形与全等三角形
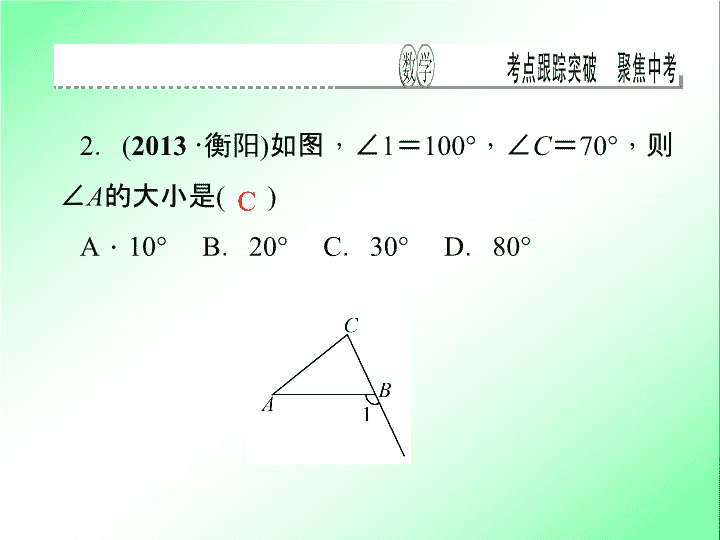
考点跟踪突破 20 三角形与全等三角形 一、选择题 ( 每小题 6 分 , 共 30 分 ) 1 . ( 2014 · 邵阳 ) 如图 , 在 △ ABC 中 , ∠ B = 46° , ∠ C = 54° , AD 平分 ∠ BAC , 交 BC 于点 D , DE ∥ AB , 交 AC 于点 E , 则 ∠ ADE 的大小是 ( ) A . 45° B . 54° C . 40° D . 50° C 2 . ( 2013 · 衡阳 ) 如图 , ∠ 1 = 100° , ∠ C = 70° , 则 ∠ A 的大小是 ( ) A . 10° B . 20° C . 30° D . 80° C 3 . ( 2012 · 南通 ) 如图 , 在 △ ABC 中 , ∠ C = 70° , 沿图中虚线截去 ∠ C , 则 ∠ 1 + ∠ 2 = ( ) A . 360° B . 250° C . 180° D . 140° B 4 . ( 2014 · 威海 ) 如图 , 在 △ ABC 中 , ∠ ABC = 50° , ∠ ACB = 60° , 点 E 在 BC 的延长线上 , ∠ ABC 的平分线 BD 与 ∠ ACE 的平分线 CD 相交于点 D , 连接 AD , 下列结论中不正确的是 ( ) A . ∠ BAC = 70° B . ∠ DOC = 90° C . ∠ BDC = 35° D . ∠ DAC = 55° B 5 . ( 2013 · 铁岭 ) 如图,在 △ ABC 和 △ DEC 中 , 已知 AB = DE , 还需添加两个条件才能使 △ ABC ≌△ DEC , 不能添加的一组条件是 ( ) A . BC = EC , ∠ B = ∠ E B . BC = EC , AC = DC C . BC = DC , ∠ A = ∠ D D . ∠ B =∠ E , ∠ A =∠ D C 二、填空题 ( 每小题 6 分 , 共 30 分 ) 6 . ( 2014 · 广州 ) 在 △ ABC 中 , 已知 ∠ A = 60° , ∠ B = 80° , 则 ∠ C 的外角的度数是 . 7 . ( 2014 · 长沙 ) 如图 , 点 B , E , C , F 在一条直线上 , AB ∥ DE , AB = DE , BE = CF , AC = 6 , 则 DF = ____ . 140° 6 8 . ( 2013 · 白银 ) 如图 , 已知 BC = EC , ∠ BCE = ∠ ACD , 要使 △ ABC ≌△ DEC , 则应添加的一个条件为 . ( 答案不唯一 , 只需填一个 ) AC = DC( 答案不唯一 ) 9 . ( 2012 · 乐山 ) 如图 , ∠ ACD 是 △ ABC 的外角 , ∠ ABC 的平分线与 ∠ ACD 的平分线交于点 A 1 , ∠ A 1 BC 的平分线与 ∠ A 1 CD 的平分线交于点 A 2 , … , ∠ A n - 1 BC 的平分线与 ∠ A n - 1 CD 的平分线交于点 A n , 设 ∠ A = θ. 则: (1) ∠ A 1 = ____ ; (2) ∠ A n = ____ . 10 . ( 2012 · 黄石 ) 将下列正确命题的序号填在横线上 ____ . ① 若 n 为大于 2 的正整数 , 则 n 边形的所有外角之和为 (n - 1) · 180° ; ② 三角形的三条中线的交点就是三角形的重心; ③证明两个三角形全等的方法有: SSS , SAS , ASA , SSA 及 HL 等. ② 三、解答题 ( 共 40 分 ) 11 . (10 分 ) ( 2014 · 武汉 ) 如图 , AC 和 BD 相交于点 O , OA = OC , OB = OD. 求证: DC ∥ AB. 12 . (10 分 ) ( 2014 · 宜宾 ) 如图 , 在 △ AFD 和 △ CEB 中 , 点 A , E , F , C 在同一直线上 , AE = CF , ∠ B = ∠ D , AD ∥ BC. 求证: AD = BC. 13 . (10 分 ) ( 2013 · 佛山 ) 课本指出:公认的真命题称为公理 , 除了公理外 , 其他的真命题 ( 如推论、定理等 ) 的正确性都需要通过推理的方法证实. (1) 叙述三角形全等的判定方法中的推论 AAS ; (2) 证明推论 AAS . 要求:叙述推论用文字表达;用图形中的符号表达已知、求证 , 并证明 , 证明对各步骤要注明依据. 解: (1) 三角形全等的判定方法中的推论 AAS 指的是:两角及其中一 角的对边对应相等的两个三角形全等 (2) 已知:在 △ ABC 与 △ DEF 中 , ∠ A = ∠ D , ∠ C = ∠ F , B C = EF. 求证: △ ABC ≌△ DEF. 证明:如图 , 在 △ ABC 与 △ DEF 中 , ∠ A = ∠ D , ∠ C = ∠ F( 已知 ) , ∴∠ A + ∠ C = ∠ D + ∠ F ( 等量代换 ) .又 ∵∠ A + ∠ B + ∠ C = 180 ° , ∠ D + ∠ E + ∠ F = 180 ° ( 三角形内角和 定理 ) , ∴∠ B = ∠ E , ∴ 在 △ ABC 与 △ DEF 中 , î ï í ï ì ∠ C = ∠ F , BC = EF , ∠ B = ∠ E , ∴△ ABC ≌△ DEF ( ASA ) 14 . (10 分 ) ( 2014 · 杭州 ) 在 △ ABC 中 , AB = AC , 点 E , F 分别在 AB , AC 上 , AE = AF , BF 与 CE 相交于点 P. 求证: PB = PC , 并直接写出图中其他相等的线段. 解:在 △ ABF 和 △ ACE 中 , î ï í ï ì AB = AC , ∠ BAF = ∠ CAE , AF = AE , ∴△ ABF ≌△ ACE ( SAS ) , ∴∠ ABF = ∠ ACE( 全等三角形的对应角相等 ) , ∴ BF = CE( 全等三角形的对应边相等 ) , ∵ AB = AC , AE = AF , ∴ BE = CF , 在 △ BEP 和 △ CFP 中 , î ï í ï ì ∠ BPE = ∠ CPF , ∠ PBE = ∠ PCF , BE = CF , ∴△ BEP ≌△ CFP ( AAS ) , ∴ PB = PC , ∵ BF = CE , ∴ PE = PF , ∴ 图中相等的线段为 PE = PF , BE = CF查看更多