最新人教版七年级数学下册精品课件第六章 实 数小结与复习

最新人教版七年级数学下册精品课件第六章 实 数小结与复习

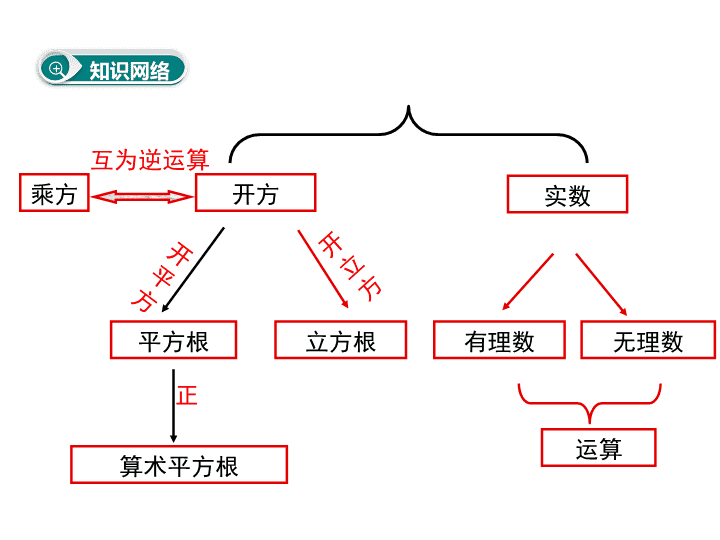
小结与复习 知识网络 专题复习 课堂小结 课后训练 第六章 实 数 正 知识网络 乘方 开方 平方根 立方根 开 平 方 开 立 方 互为逆运算 算术平方根 实数 有理数 无理数 运算 专题复习 【例1】1.求下列各数的平方根： 225 1(1) ; (2) 6 ; (3) ( 10)36 4  2.求下列各数的立方根： 8(1) 2125 - 7；（ ）0.027；（3）1- 8 【归纳拓展】解题时，要注意题目的要求，是求平方 根、立方根还是求算术平方根. 专题一 开方运算 5(1) ;6  5(2) ;2  (3) 10. 2(1) ;5  (2) 0.3; 1(3) .2 【迁移应用1】求下列各式的值： 400 ;① 16 81 ② 49 100 ③ 3 631 64  ④ 答案：① 20；② ；③ ；④ .4 9  7 10  1 4  【例2】在-7.5， , 4, , , , 中，无理数 的个数是（ ） 0.15   A. 1个 B. 2个 C.3个 D.4个 【归纳拓展】对实数进行分类不能只看表面形式， 应先化简，再根据结果去判断. B 专题二 实数的有关概念 【迁移应用2】（1）在- ，0.618， ， ， 中， 负有理数的个数是（ ） A. 1个 B. 2个 C.3个 D.4个 A A. 1个 B. 2个 C.3个 D.4个 （2）下列实数 ， , ,3.14159， ，- 中， 正分数的个数是（ ）B 【注意】 ， 等不属于分数，而是无理数. 【例3】(1) 位于整数 和 之间. (2)实数a,b在数轴上的位置如图所示，化简 = . a 0 b -2a 【归纳拓展】 1.实数与数轴上的点是一一对应的关系； 2.在数轴上表示的数，右边的数总是比左边的 数大. 专题三 实数的估算及与数轴的结合 20 4 5 【迁移应用3】如图所示，数轴上与1， 对应的点 分别是为A、B，点B关于点A的对称点为C,设点C表示 的数为x,则 = . 0 1 2 BC A 2 2 22x 【例4】（1） （2） 60 y-1 【例5】已 知 ， ， ,则 = ， = . 0.08138 37.77 【例6】计算： = . 专题四 实数的运算 【归纳拓展】开立方运算时要注意小数点的变化规律，开立方 是三位与一位的关系，开平方是二位与一位的关系. 【迁移应用4】计算： 答案：（1）5.79；（2）5.48 课堂小结 1.通过对本章内容的复习，你认为平方根和立方根之 间有怎么样的区别与联系？ 2.什么是实数？ 3.实数的运算法则与有理数的运算法则有什么联系？ 课后训练 1.写出两个大于1小于4的无理数____、____. 2. 的整数部分为____,小数部分为_ ____.10 3.一个立方体的棱长是4cm，如果把它体积扩大为 原来的8倍,则扩大后的立方体的表面积是_______. 10 3 2 π 3 2384cm 4.求下列各式中的x. （1） (x-1)2=64； （2） 3 729 02 x      (x=9或-7 ) (x=-18) 5.比较大小： 与 .52 32 解：∵(-2+ )-(-2+ )= -2+ +2- = - ＞0 ∴-2+ ＞-2+ 另解：直接由正负决定-2+ ＞-2+5 35 3 5 3 5 3 5 3 6.若 ,0)34(43 2  ba 求-ab 的平方根. 解：∵｜3a+4｜≥0且(4b-3)2≥0 而｜3a+4｜+(4b-3)2=0 ∴｜3a+4｜=0且(4b-3)2=0 ∴a= ，b= . ∴-ab=-( × )=1 , ∴ 1 的平方根是±1. 3 4 4 3 3 4 4 3 7.计算：   ;8136.0)1( 32016  .642 1 16 1)2( 3 2      解：原式=3.6； 解：原式=-4.