- 2021-02-26 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
5年级数学教案《3的倍数的特征》
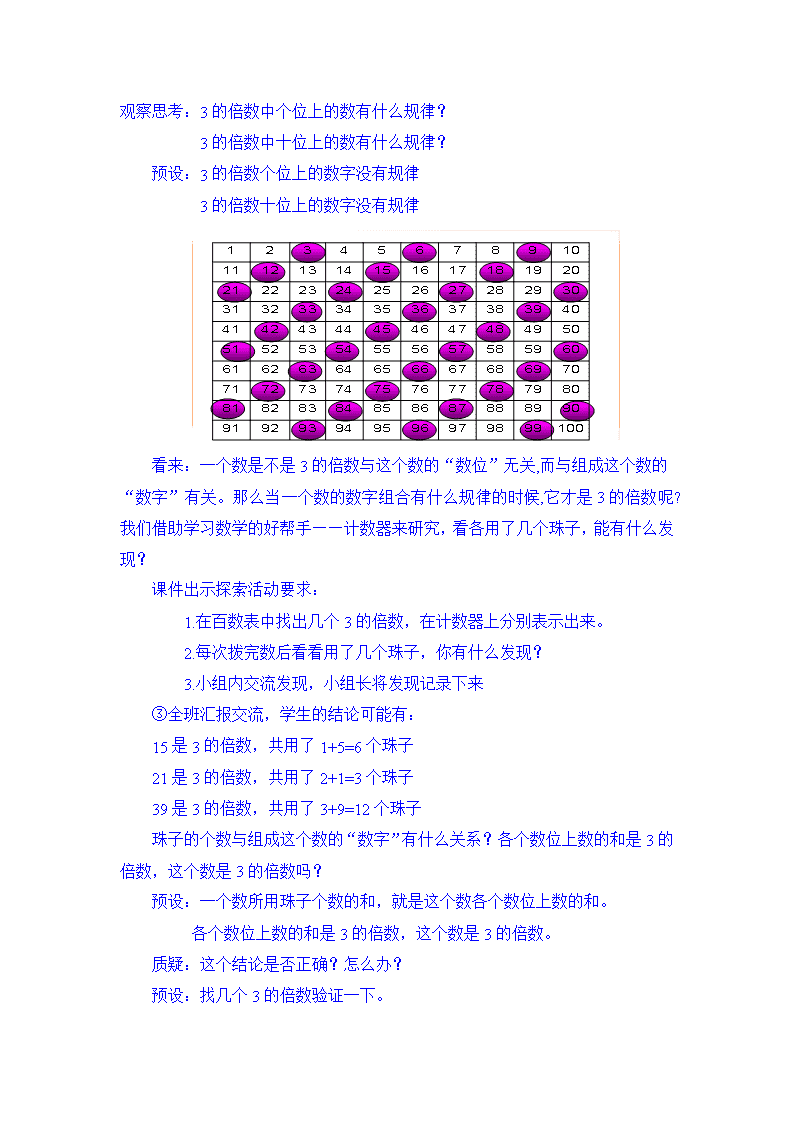
3的倍数的特征 教学内容: 小学数学五年级上册92页信息窗2第2课时 教学目标: 1.通过观察、探究、交流等活动,经历探索3的倍数特征的过程。掌握3的倍数特征,能正确判断一个数是不是3的倍数,培养学生的数感。 2.体会探索数的特征的一些方法,能通过列举——猜想——验证——结论这一过程发现3的倍数的特征,进一步提高学生的合情推理能力以及数学表达的能力。 3.在探索数的有关特征的过程中,体会数学内容的奇妙、有趣,激发对数学的好奇心和求知欲,获得积极的情感体验,进一步提高学好数学的信心。 教学重难点: 教学重点:3的倍数的特征;会判断一个数是不是3的倍数 教学难点:经历3的倍数特征的探究过程;理解为什么要看“各个数位上数的和是不是3的倍数”的道理 教学具准备: 教师准备:课件、计数器、探究特征表格、百数表、小棒图等 学生准备:计数器、计算器 教学过程: 一、创设情境,导入新知 谈话:同学们,我们在上节课一起欣赏了交谊舞和圆圈舞的团体舞蹈表演,利用“列举法”和“百数表”探究了2和5的倍数的特征。 (1) 2的倍数的特征是什么? (2) 5的倍数的特征是什么? (3)你能判断下面的数哪些是2的倍数?哪些是5的倍数? 12 57 50 45 126 355 1248 让学生回答并说出判断依据,从而小结:我们在判断一个数是否是2、5的倍数,都是从一个数的个位上的情况来判定。 我们下面再来看看叠罗汉的精彩表演。(多媒体课件出示部分信息窗情境图) 观察情境图,从中能发现什么信息? 预设:叠罗汉都是3人一组。 如果让你安排表演,可以选派几组表演,多少人参加?请你说出组数、人数和算式。预设: 派一个组、3人、3×1﹦3。(板书:3) 派二个组、6人、3×2﹦6。(板书:6) 派三个组、9人、3×3﹦9。(板书:9) 派四个组、12人、3×4﹦12。(板书:12) 请把算式藏在心里,只说人数行吗? 预设:15、18、21、24……(板书) 叠罗汉的人数都与哪个数有关?有怎样的关系? 预设:都与3有关,是3的倍数。 我们学习了2和5的倍数的特征,那么3的倍数有没有它自己的特征呢?这节课只要你认真观察、积极思考,就一定会发现其中的奥秘。下面我们就一起来研究3的倍数特征。(板书课题:3的倍数特征) 二、自主学习,小组探究 1.猜测特征。 同学们,3的倍数有什么特征呢?可以大胆猜想一下! 预设:也许受2、5倍数特征的影响,学生大多会从数的个位上的数字进行研究,学生可能猜测:个位上是3、6、9的数是3的倍数。 这个结论成立不成立呢?只观察一个数的个位数字能确定这个数是3的倍数吗? 2.探究特征。 3的倍数到底有什么特征呢?下面我们借助百数表来帮忙研究。 出示百数表 ①谈话:把“百数表”中3的倍数圈出来研究研究。(学生人手一份十行十列的百数表) ②3的倍数已经用红色表示出来了, 先验证刚才的猜测是否正确?课件演示,观察思考:3的倍数中个位上的数有什么规律? 3的倍数中十位上的数有什么规律? 预设:3的倍数个位上的数字没有规律 3的倍数十位上的数字没有规律 看来:一个数是不是3的倍数与这个数的“数位”无关,而与组成这个数的“数字”有关。那么当一个数的数字组合有什么规律的时候,它才是3的倍数呢?我们借助学习数学的好帮手——计数器来研究,看各用了几个珠子,能有什么发现? 课件出示探索活动要求: 1.在百数表中找出几个3的倍数,在计数器上分别表示出来。 2.每次拨完数后看看用了几个珠子,你有什么发现? 3.小组内交流发现,小组长将发现记录下来 ③全班汇报交流,学生的结论可能有: 15是3的倍数,共用了1+5=6个珠子 21是3的倍数,共用了2+1=3个珠子 39是3的倍数,共用了3+9=12个珠子 珠子的个数与组成这个数的“数字”有什么关系?各个数位上数的和是3的倍数,这个数是3的倍数吗? 预设:一个数所用珠子个数的和,就是这个数各个数位上数的和。 各个数位上数的和是3的倍数,这个数是3的倍数。 质疑:这个结论是否正确?怎么办? 预设:找几个3的倍数验证一下。 45,4+5=9,9是3的倍数。45也是3的倍数。 57,5+7=12,12是3的倍数。57也是3的倍数。 123,1+2+3=6,,6是3的倍数。123也是3的倍数。 质疑:如果一个数不是3的倍数,这个数各位上数的和会是3 的倍数吗? 请同学们任意找几个数算一算,再将研究结果在小组里交流。(学生活动) 预设:35,3+5=8,8不是3的倍数。35也不是3的倍数。 74,7+4=11,11不是3的倍数。74也不是3的倍数。 235, 2+3+5=10,10不是3的倍数。235也不是3的倍数。 小结:像上面的数,十位与个位上的数加起来的和是3的倍数时,这个数就是3的倍数;十位与个位上的数加起来的和不是3的倍数时,这个数就不是3的倍数。 3.试一试,下面的数,是3的倍数打√,不是3的倍数的打×。 87 32 231 121 1924 ( ) ( ) ( ) ( ) ( ) 三、掌握算理、评价质疑 1.质疑、释疑。我们研究出了3的倍数的特征,你有什么疑问吗? (1)预设:我们知道了2和5的倍数的特征为什么只看个位的道理,3的倍数的特征为什么要看一个数各个数位上数的和? 为什么各个数位上的数的和是3的倍数,这个数就是3的倍数呢? (2)释疑。以45为例引导分析。 45是3的倍数吗?(4+5﹦9,9是3的倍数,45是3的倍数), 4+5中的5,本来是4个十加5个一,,判断时却变成了4个一加5个一。像上节课分析2的倍数那样,你找到4个一吗? 学生借助小棒图,以小组为单位自主分析。 学生汇报展示、交流。 教师课件演示(如下图):45是4个十和5个一,从1个十中把3的倍数拿走,拿走了9个,9是3的倍数,就不要看了,还剩1个。4个十共剩4个一。 再以57为例,57是5个十和7个一,从1个十中把3的倍数拿走,拿走了9个,9是3的倍数,就不要看了,还剩1个。5个十共剩5个一。 再出示123的小棒图,如果百位上是1,表示100,从100里拿走3的倍数,拿走了99个,还剩下1个,十位上2拿走3的倍数还剩下2个……同学们看,数位上的数与剩下的数是什么关系? 预设:数位上的数与剩下的数是一样的。 教师小结:实际上我们加的就是剩下的数,而剩下的数与数位上的数正好一样,所以判断3的倍数,我们就把数位上的数相加。 3.形成结论: 3的倍数的确与各个数位上的数有关!一个数不论大小,只要各个数位上数的和是3的倍数,这个数就是3的倍数。(板书) 四、抽象概括、总结提升 同学们,我们这么快就找到了3的倍数的特征,回想一下,我们是怎样研究3的倍数的特征的?。 列举——猜想——验证——结论。(板书)这是一条科学探究之路! 你知道吗,为了便于研究3的倍数的特征,我们采取了一个小小的策略。别小看这个小小的策略,她却是赫赫有名的“比较法” !(板书:比较法)在初步发现结论后,通过大量举例进行了验证,最后形成了结论。这种由个别到一般的研究方法,就是我们经常用到的 “归纳法” 。(板书:归纳法) 五、巩固练习 1.基本练习。(课本95页自主练习第3题) 学生判断时注意说说判断的依据。学生利用特征判断后,教学生快速判断法,比如49只看4就知道它不是3的倍数,引导学生发现:遇到数字本身是3的倍数时,可以略去不加,如1236,只要算1+2=3即可判断1236是3的倍数。 (这是一个基本练习,使全体学生都能对新知识有进一步的理解,达到巩固新知的目的。) 2.综合练习(课本95页自主练习第4题) 分析:这是一道解决实际问题的题目。 建议:根据2、5、3的倍数的特征,学生自主完成,集体评议。重点说出剩余与不剩余的理由。 预设:没有剩余,因为每3人一组,45正好是3的倍数。 没有剩余,因为每5人一组,50正好是5的倍数。 有剩余,因为每2人一组,35不是2的倍数。 3. 拓展练习. 课本95页自主练习第7题 (这是一个综合练习,以检验学生综合运用知识的能力,达到举一反三的效果,提高思维的灵活性。) 建议:练习时,先引导学生明确要求,从4个数字中任意选择两个数字,组合成符合要求的两位数,再让学生独立完成,为了照顾学生之间的差异,在交流时,可以先让有困难的学生提出遇到的问题,由大家质疑,并提出好的解题方法。 4.拓展延伸。□里能填几? (1)3的倍数: (2)2的倍数: (3)5的倍数: 6 13 8 34 0 此题是一道稍微复杂的问题。练习时,让学生独立分析解决问题,交流时说清楚思路。 关注此题解法的多样性: 七、课堂小结: 同学们,通过这节课的学习,你在知识的掌握、数学活动经验的积累、解决问题的策略等方面,有哪些新的收获?课后可以用今天的研究方法,研究一下9的倍数的特征。 板书设计: 3的倍数的特征 3、6、9、12、15、18、21、24…… 一个数,各个数位上数的和是3的倍数, 这个数就是3的倍数。 列举——猜想——验证——结论: 比较法 归纳法 设计说明 1.亮点。回味课堂,我感觉亮点之处有: (1)关注结果,更关注过程。 由2和5倍数的特征到3的倍数的特征,由观察个位上的数到观察各个数位上数的和,对学生来说思维的跨度确实是大了些。教学时从学生喜闻乐见的“叠罗汉”表演情境入手,列举出3的倍数。在观察的基础上,引发认知冲突,再进行大胆猜想。用计数器通过拨数,从正反两个方面加以探究验证,形成初步结论。“我们知道了12、18、24、48具备是3的倍数这一特征,其它3的倍数是否也具备这个特征呢?”,进而举例验证结论。学生经历了“列举——猜想——验证——结论”的较为完整的探究过程,使学生进一步积累和丰富数学活动经验。 (2)注重培养学生敢于质疑的良好品质。 当学生探究出3的倍数特征后,通过质疑——“3的倍数特征为什么要看各个数位上数的和?”学生不仅要知其然,还要知其所以然,使学生的思维向深度发展。 2.困惑。 课堂上怎样既为学生提供充分发言的机会,又能有效地完成教学目标? 3.使用建议。 猜想3的倍数到底与什么有关时,学生可能猜想不出来,教师有必要直接给出“是否与各个数位上数的和有关呢?”这一问题,以便尽早把研究内容定向,把教学重点放在探究3的倍数的特征上来。练习题的设计也应形式多样化,这样效率更高。 查看更多