高考数学专题复习教案： 正弦定理和余弦定理

高考数学专题复习教案： 正弦定理和余弦定理

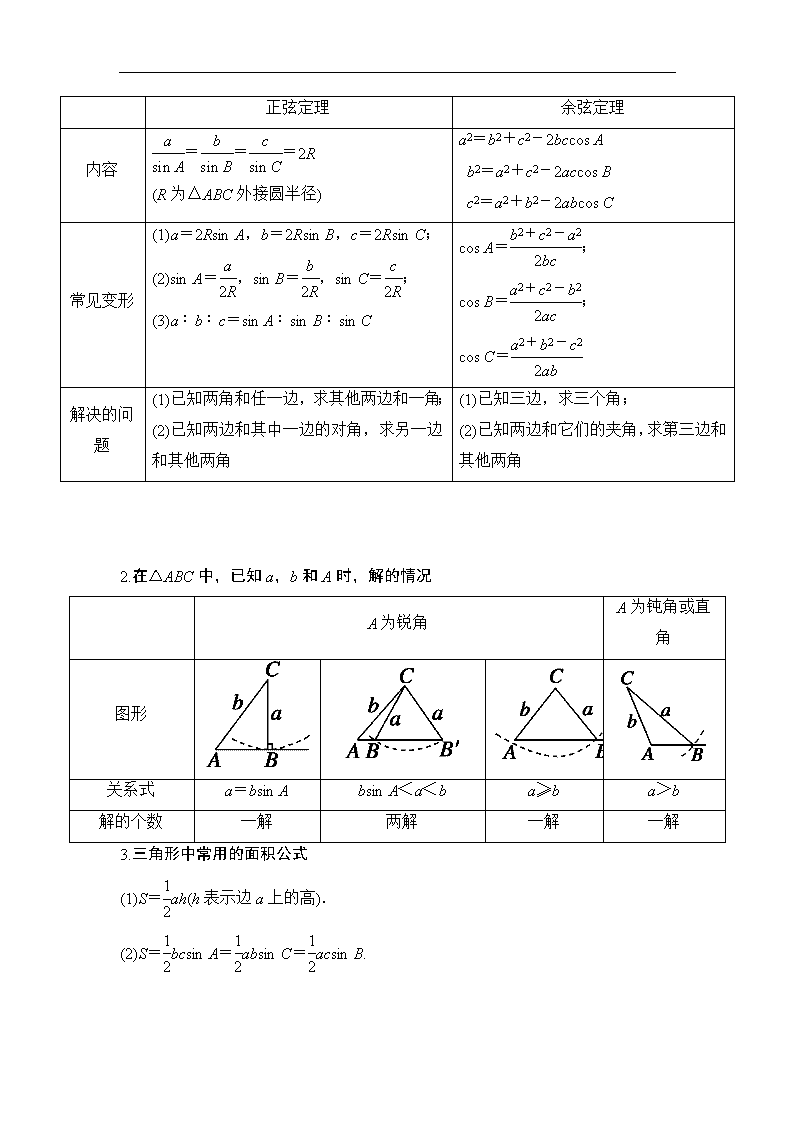
正弦定理和余弦定理 主标题：正弦定理和余弦定理 副标题：为学生详细的分析正弦定理和余弦定理的高考考点、命题方向以及规律总结。‎ 关键词：正弦定理，余弦定理 难度：3‎ 重要程度：5‎ 考点剖析：‎ 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.‎ 命题方向：‎ ‎1．正、余弦定理与三角形面积的综合问题是每年高考的重点内容，既有选择、填空题，也有解答题，难度适中，属中档题．‎ ‎2．高考对此类问题的考查主要有以下两个命题角度：‎ ‎(1)求三角形的面积；‎ ‎(2)已知三角形的面积解三角形．‎ 规律总结：‎ 1组关系——三角形中的边角关系 ‎　在△ABC中，A＞B⇔a＞b⇔sin A＞sin B⇔cos A＜cos B.‎ 2种途径——判断三角形形状的途径 ‎　根据所给条件确定三角形的形状，主要有两种途径：‎ ‎(1)化边为角；(2)化角为边，并常用正弦(余弦)定理实施边、角转换．‎ 2个注意点——解三角形应注意的问题 ‎　(1)在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解或无解，所以要进行分类讨论．‎ ‎(2)在判断三角形形状时，等式两边一般不要约去公因式，应移项提取公因式，以免漏解．‎ 知 识 梳 理 ‎1．正弦定理和余弦定理 在△ABC中，若角A，B，C所对的边分别是a，b，c，则 正弦定理 余弦定理 内容 ＝＝＝2R ‎(R为△ABC外接圆半径)‎ a2＝b2＋c2－2bccos A ‎ b2＝a2＋c2－2accos B ‎ c2＝a2＋b2－2abcos C 常见变形 ‎(1)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；‎ ‎(2)sin A＝，sin B＝，sin C＝；‎ ‎(3)a∶b∶c＝sin A∶sin B∶sin C cos A＝；‎ cos B＝；‎ cos C＝ 解决的问题 ‎(1)已知两角和任一边，求其他两边和一角；‎ ‎(2)已知两边和其中一边的对角，求另一边和其他两角 ‎(1)已知三边，求三个角；‎ ‎(2)已知两边和它们的夹角，求第三边和其他两角 ‎2.在△ABC中，已知a，b和A时，解的情况 A为锐角 A为钝角或直角 图形 关系式 a＝bsin A bsin A＜a＜b a≥b a＞b 解的个数 一解 两解 一解 一解 ‎3.三角形中常用的面积公式 ‎(1)S＝ah(h表示边a上的高)．‎ ‎(2)S＝bcsin A＝absin C＝acsin B.‎ ‎(3)S＝r(a＋b＋c)(r为△ABC内切圆半径)．‎