【数学】2019届一轮复习北师大版集合、常用逻辑用语学案
专题一 集合、常用逻辑用语、不等式、函数与导数
第一讲 集合、常用逻辑用语
高考导航
高考对集合的考查主要是集合的含义、集合之间的基本关系和集合的运算,并且以集合的运算为主.试题往往与不等式的解集、函数的定义域、方程的解集、平面上的点集等相互交汇,试题难度不大.
2.高考对常用逻辑用语的考查主要是命题、充要条件、逻辑联结词和量词,并且以充要条件的判断、命题真假的判断为主,对含有量词的命题的否定也是一个值得注意的考点.
1.(2017·全国卷Ⅲ)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1 B.2 C.3 D.4
[解析] A∩B={2,4},所以元素个数为2,故选B.
[答案] B
2.(2017·北京卷)已知全集U=R,集合A={x|x<-2或x>2},则∁UA=( )
A.(-2,2) B.(-∞,-2)∪(2,+∞)
C.[-2,2] D.(-∞,-2]∪[2,+∞)
[解析] ∁UA={x|-2≤x≤2}=[-2,2].
[答案] C
3.(2017·天津卷)设θ∈R,则“<”是“sinθ<”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
[解析] ∵<⇔-<θ-<⇔0<θ<,
sinθ<⇔θ∈,k∈ ,,k∈ ,
∴“<”是“sinθ<”的充分而不必要条件.
[答案] A
4.(2017·河北石家庄一模)下列选项中,说法正确的是( )
A.若a>b>0,则lna
(n+2)·2n-1”的否定是“∀n∈N*,3n≥(n+2)·2n-1”
D.已知函数f(x)在区间[a,b]上的图象是连续不断的,则命题“若f(a)·f(b)<0,则f(x)在区间(a,b)内至少有一个零点”的逆命题为假命题
[解析] ∵函数y=lnx(x>0)是增函数,∴若a>b>0,则lna>lnb,故A错误;若a⊥b,则m+m(2m-1)=0,解得m=0,故B错误;命题“∀n∈N*,3n>(n+2)·2n-1”的否定是“∃n∈N*,3n≤(n+2)·2n-1”,故C错误;命题“若f(a)·f(b)<0,则f(x)在区间(a,b)内至少有一个零”的逆命题“若f(x)在区间(a,b)内至少有一个零点,则f(a)·f(b)<0”是假命题,如函数f(x)=x2-2x-3在区间[-2,4]上的图象连续不断,且在区间(-2,4)内有两个零点,但f(-2)·f(4)>0,故D正确.故选D.
[答案] D
5.(2017·北京西城二模)若“x>1”是“不等式2x>a-x成立”的必要而不充分条件,则实数a的取值范围是________.
[解析] 不等式2x>a-x⇔2x+x>a⇔(2x+x)min>a,又因为函数f(x)=2x+x为增函数,所以当x>1时,(2x+x)min>3,所以a>3.
[答案] a>3
考点一 集合的关系与运算
集合的运算性质及重要结论
(1)A∪A=A,A∪∅=A,A∪B=B∪A.
(2)A∩A=A,A∩∅=∅,A∩B=B∩A.
(3)A∩(∁UA)=∅,A∪(∁UA)=U.
(4)A∩B=A⇔A⊆B,A∪B=A⇔B⊆A.
[对点训练]
1.(2017·全国卷Ⅰ)已知集合A={x|x<2},B={x|3-2x>0},则( )
A.A∩B= B.A∩B=∅
C.A∪B= D.A∪B=R
[解析] 由3-2x>0,得x<,所以B=,故A∩B=,A∪B={x|x<2}.故选A.
[答案] A
2.(2017·河北邯郸模拟)集合A={x|-2≤x≤2},B={y|y=,0≤x≤4},则下列关系正确的是( )
A.A⊆∁RB B.B⊆∁RA
C.∁RA⊆∁RB D.A∪B=R
[解析] 依题意得B={y|0≤y≤2},因此B⊆A,∁RA⊆∁RB,选C.
[答案] C
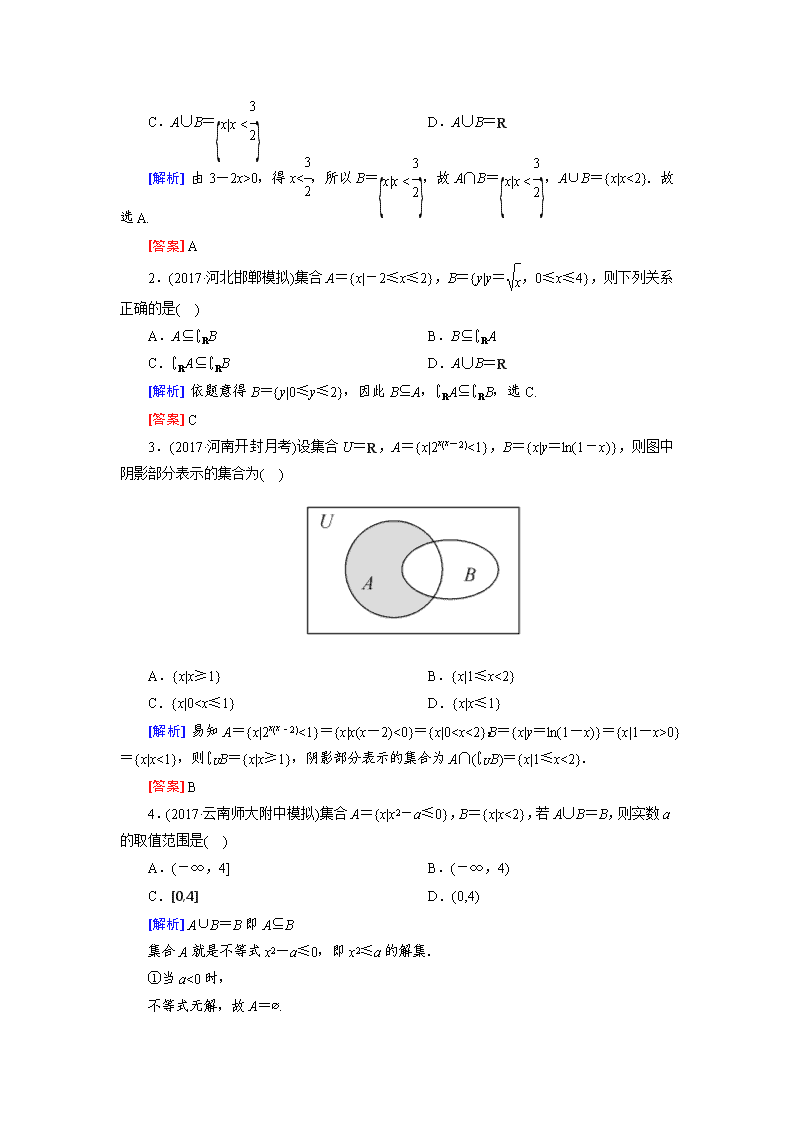
3.(2017·河南开封月考)设集合U=R,A={x|2x(x-2)<1},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
A.{x|x≥1} B.{x|1≤x<2}
C.{x|00}={x|x<1},则∁UB={x|x≥1},阴影部分表示的集合为A∩(∁UB)={x|1≤x<2}.
[答案] B
4.(2017·云南师大附中模拟)集合A={x|x2-a≤0},B={x|x<2},若A∪B=B,则实数a的取值范围是( )
A.(-∞,4] B.(-∞,4)
C.[0,4] D.(0,4)
[解析] A∪B=B即A⊆B
集合A就是不等式x2-a≤0,即x2≤a的解集.
①当a<0时,
不等式无解,故A=∅.
此时显然满足A⊆B.
②当a=0时,不等式为x2≤0,解得x=0,所以A={0}.
显然{0}⊆{x|x<2},即满足A⊆B.
③当a>0时,解不等式x2≤a,得-≤x≤.所以A=[-,].
由A⊆B可得,<2,解得0a+1或x3(x-m)”是“x2+3x-4<0”的必要不充分条件,则实数m的取值范围为________.
[解析] 由(x-m)2>3(x-m),得(x-m)(x-m-3)>0,即x>m+3或x3(x-m)”是“x2+3x-4<0”的必要不充分条件,所以m+3≤-4或m≥1,解得m≤-7或m≥1,即实数m的取值范围为(-∞,-7]∪[1,+∞).
[答案] (-∞,-7]∪[1,+∞)
考点三 命题的真假判断与否定
1.四种命题的关系
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
2.复合命题真假的判断方法
含逻辑联结词的命题的真假判断:“p∨q”有真则真,其余为假;“p∧q”有假则假,其余为真;“綈p”与“p”真假相反.
3.全称量词与存在量词
(1)全称命题p:∀x∈M,p(x),它的否定綈p:∃x0∈M,綈p(x0).
(2)特称命题p:∃x0∈M,p(x0),它的否定綈p:∀x∈M,綈p(x).
[对点训练]
1.(2017·安徽马鞍山模拟)命题“若△ABC有一内角为,则△ABC的三内角成等差数列”的逆命题( )
A.与原命题同为假命题
B.与原命题的否命题同为假命题
C.与原命题的逆否命题同为假命题
D.与原命题同为真命题
[解析] 原命题显然为真,原命题的逆命题为“若△ABC的三内角成等差数列,则△ABC有一内角为”,它是真命题.
[答案] D
2.(2017·西安质量检测)已知命题p:∃x∈R,log2(3x+1)≤0,则( )
A.p是假命题;綈p:∀x∈R,log2(3x+1)≤0
B.p是假命题;綈p:∀x∈R,log2(3x+1)>0
C.p是真命题;綈p:∀x∈R,log2(3x+1)≤0
D.p是真命题;綈p:∀x∈R,log2(3x+1)>0
[解析] ∵3x>0,∴3x+1>1,则log2(3x+1)>0,∴p是假命题;綈p:∀x∈R,log2(3x+1)>0.故选B.
[答案] B
3.(2017·山东卷)已知命题p:∃x∈R,x2-x+1≥0;命题q:若a2-2,所以q命题为假,綈q为真.
所以p∧綈q为真,p∧q,綈p∧q,綈p∧綈q皆为假,故选B.
[答案] B
4.已知命题p:函数f(x)=2ax2-x-1在(0,1)内恰有一个零点;命题q:函数y=x2-a在(0,+∞)上是减函数.若p∧(綈q)为真命题,则实数a的取值范围是________.
[解析] 对于命题p,令f(0)·f(1)<0,则-1·(2a-2)<0,解得a>1;对于命题q,令2-a<0,则a>2,故綈q对应的a的取值范围是(-∞,2].因为p∧(綈q)为真命题,所以实数a的取值范围是(1,2].
[答案] (1,2]
解决命题的判定问题应注意的3点
(1)判断四种命题真假有下面两个途径,一是先分别写出四种命题,再分别判断每个命题的真假;二是利用互为逆否命题是等价命题这一关系来判断它的逆否命题的真假.
(2)要判定一个全称命题是真命题,必须对限定集合M中的每个元素x验证p(x)成立.要判定一个特称(存在性)命题是真命题,只要在限定集合M中,至少能找到一个x=x0,使p(x0)成立即可.
(3)含有量词的命题的否定,需从两方面进行:一是改写量词或量词符号;二是否定命题的结论,两者缺一不可.
热点课题1 集合中的新定义问题
[感悟体验]
1.(2017·山西四校联考)已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“Ω集合”.给出下列4个集合:
①M=;
②M=;
③M={(x,y)|y=cosx};
④M={(x,y)|y=lnx}.
其中是“Ω集合”的所有序号为( )
A.②③ B.③④
C.①②④ D.①③④
[解析] 对于①,若x1x2+y1y2=0,则x1x2+·=0,即(x1x2)2=-1,可知①错误;对于④,取(1,0)∈M,且存在(x2,y2)∈M,则x1x2+y1y2=1×x2+0×y2=x2>0,可知④错误.同理,可证得②和③都是正确的.故选A.
[答案] A
2.(2017·济南一模)已知集合A={0,1},B={a2,2a},其中a∈R,记A⊙B={x|x=x1+x2,x1∈A,x2∈B},若集合A⊙B中的最大元素是2a+1,则a的取值范围为________.
[解析] 由题意可知a2,2a,a2+1,2a+1中2a+1最大,所以2a+1>a2+1,解得0
查看更多