数学冀教版九年级上册教案26-4解直角三角形的应用

数学冀教版九年级上册教案26-4解直角三角形的应用

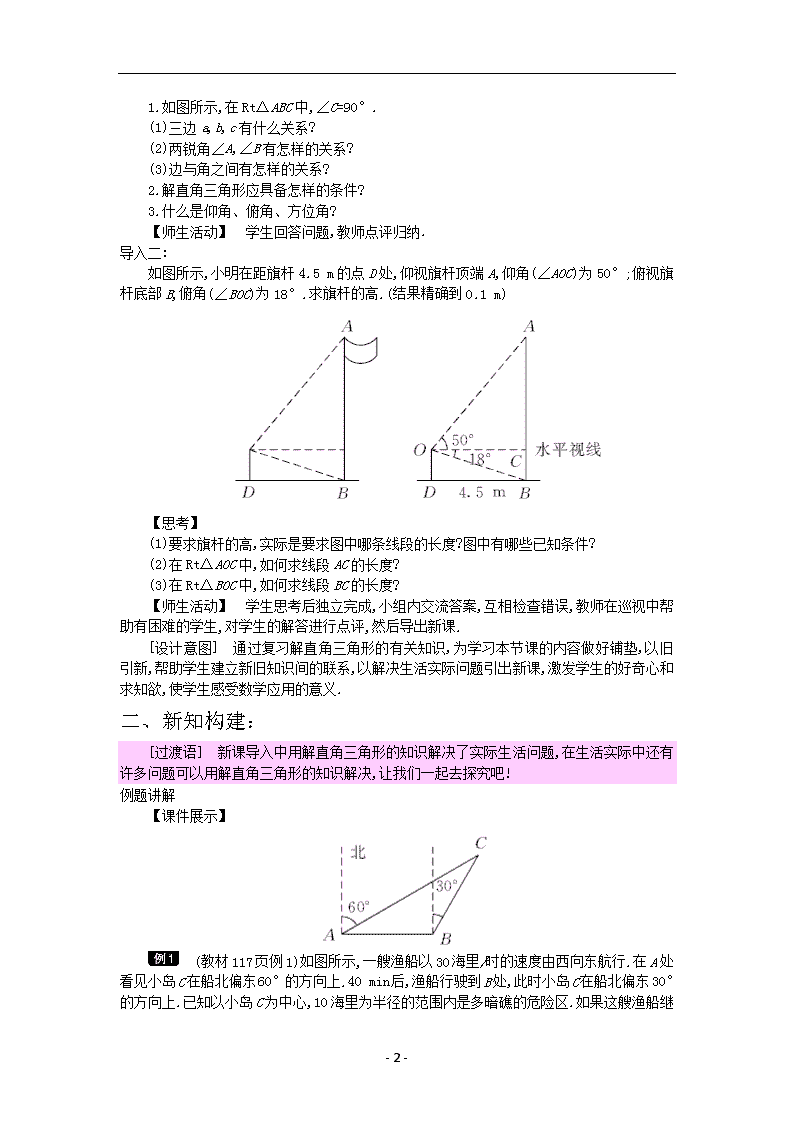
- 1 - 26.4 解直角三角形的应用 教学目标 【知识与能力】 1.了解仰角、俯角、方位角、坡度、坡角等有关概念,知道坡度与坡角之间的关系. 2.经历用三角函数解决问题的过程,能够把实际问题转化为数学问题,进一步体会三角函数 在解决问题过程中的作用. 3.能够借助计算器进行有关三角函数的计算,并能对结果的意义进行说明. 4.通过在具体情境中,从数学的角度发现问题和提出问题,并综合运用数学知识解决简单的 实际问题. 【过程与方法】 1.通过画示意图,将实际问题转化为数学问题,培养学生的抽象概括能力,提高应用数学知识 解决实际问题的能力. 2.经历从实际问题中建立数学模型的过程,增强应用意识,提高解决问题的能力,体会数形结 合思想的应用. 3.培养学生分析问题、解决问题的能力,提高学生思维能力的灵活性. 【情感态度价值观】 1.通过学生经历根据实际问题画示意图的过程,培养学生的动手能力,激发学生对数学的好 奇心和求知欲. 2.通过将实际问题转化为数学问题,培养建模思想,提高分析问题、解决问题的能力. 3.调动学生学习数学的积极性和主动性,培养学生认真思考等学习习惯,形成事实求是的科 学态度. 教学重难点 【教学重点】 1.用三角函数有关知识解决仰角、俯角、方位角、坡度、坡角等实际问题. 2.能根据题意画出示意图,将实际问题的数量关系转化为直角三角形元素之间的关系. 【教学难点】 正确理解题意,将实际问题转化为数学模型的过程. 课前准备 多媒体课件 教学过程 一、新课导入： 导入一: 复习提问: - 2 - 1.如图所示,在 RtΔABC 中,∠C=90°. (1)三边 a,b,c 有什么关系? (2)两锐角∠A,∠B 有怎样的关系? (3)边与角之间有怎样的关系? 2.解直角三角形应具备怎样的条件? 3.什么是仰角、俯角、方位角? 【师生活动】 学生回答问题,教师点评归纳. 导入二: 如图所示,小明在距旗杆 4.5 m 的点 D 处,仰视旗杆顶端 A,仰角(∠AOC)为 50°;俯视旗 杆底部 B,俯角(∠BOC)为 18°.求旗杆的高.(结果精确到 0.1 m) 【思考】 (1)要求旗杆的高,实际是要求图中哪条线段的长度?图中有哪些已知条件? (2)在 RtΔAOC 中,如何求线段 AC 的长度? (3)在 RtΔBOC 中,如何求线段 BC 的长度? 【师生活动】 学生思考后独立完成,小组内交流答案,互相检查错误,教师在巡视中帮 助有困难的学生,对学生的解答进行点评,然后导出新课. [设计意图] 通过复习解直角三角形的有关知识,为学习本节课的内容做好铺垫,以旧 引新,帮助学生建立新旧知识间的联系,以解决生活实际问题引出新课,激发学生的好奇心和 求知欲,使学生感受数学应用的意义. 二、新知构建： [过渡语] 新课导入中用解直角三角形的知识解决了实际生活问题,在生活实际中还有 许多问题可以用解直角三角形的知识解决,让我们一起去探究吧! 例题讲解 【课件展示】 (教材 117 页例 1)如图所示,一艘渔船以 30 海里/时的速度由西向东航行.在 A 处看见小岛 C 在船北偏东 60°的方向上.40 min 后,渔船行驶到 B 处,此时小岛 C 在船北偏东 30°的方向上.已知以小岛 C 为中心,10 海里为半径的范围内是多暗礁的危险区.如果这艘渔 - 3 - 船继续向东航行,有没有进入危险区的可能? 思路一 教师引导分析: (1)如何判断有没有进入危险区的可能? (点 C 到直线 AB 的距离与 10 海里比较大小) (2)要求点 C 到直线 AB 的距离,需要作什么辅助线? (过点 C 作 CD⊥AB,交 AB 的延长线于点 D) (3)要求 CD 的长,CD 在哪个直角三角形中? (RtΔBCD 和 RtΔACD 中) (4)RtΔBCD 和 RtΔACD 中,有什么已知条件? (RtΔBCD 中,∠CBD=60°;RtΔACD 中,∠CAD=30°) (5)解决几何计算问题时,常用什么数学思想方法? (方程思想) (6)设 CD=x,则直角三角形中的边长能否用 x 表示? ‸ = ‸ tan60 ° = 1 3 , ‸ = ‸ tan30 ° = 3(7)题目中的等量关系是什么?你能列方程求解吗? = ‸ - ‸ , 3 - 1 3 = 20(8)根据以上分析,你能写出解答过程吗? 【师生活动】 学生在教师提出的问题的引导下,思考回答,师生共同分析解题思路,学 生独立完成解答过程,教师在巡视过程中及时辅导,鼓励学生从不同的角度思考问题,最后展 示学生的解答过程,教师规范书写过程,强调方程思想在数学中的应用. 【课件展示】 解:如图所示,过点 C 作 CD⊥AB,交 AB 的延长线于点 D,则∠CBD=60°, 在 RtΔBCD 中,tan∠CBD=tan 60°= ‸ ‸ . 若设 CD=x,则 BD= ‸ tan60 ° = 1 3 x. 在 RtΔACD 中,∠CAD=30°, 所以 tan∠CAD=tan 30°= ‸ ‸ , 即 AD= ‸ tan30 ° = 3 x. 因为 AD-BD=AB,AB=30× 40 60 =20, 所以 3 x- 1 3 x=20,解得 x=10 3 . - 4 - 因为 10<10 3 ,所以这艘渔船继续向东航行,不会进入危险区. 思路二 【教师活动】 教师引导学生要判断会不会进入危险区,需要作辅助线,构造直角三角 形. 【学生活动】 根据题意画出图形,思考解题思路和方法. 【教师活动】 引导学生用方程思想解决几何中的求线段的长度问题. 【学生活动】 独立思考后,小组合作交流解题思路,完成解题过程,小组代表展示过程. 【教师活动】 教师在巡视过程中,帮助有困难的学生,对学生的展示进行点评,并规范 解题过程,强调解决实际问题的关键. 【课件展示】 同思路一. [设计意图] 通过教师引导或自主学习方式解决有关方位角的实际问题,让学生进一步 体会数形结合思想、建模思想和方程思想在数学中的应用,提高学生分析问题、解决问题的 能力,体会将实际问题转化为解直角三角形问题的一般思路和方法. 认识有关概念 【课件展示】 如图所示,通常把坡面的垂直高度 h 和水平宽度 l 的比 叫做坡面的坡度 (或坡比),坡面与水平面的夹角α叫做坡角. 【思考】 坡度 i 与坡角α之间具有什么关系? = = tan【师生活动】 学生小组合作交流,归纳结论,教师点评. 【课件展示】 (教材 118 页例 2)如图所示,铁路路基的横断面为四边形 ABCD,其中,BC∥AD,∠ A=∠D,根据图中标出的数据计算路基下底的宽和坡角(结果精确到 1'). 教师引导分析: (1)进行和坡度有关的计算,常作辅助线构造直角三角形,根据解直角三角形的知识求坡 角. (2)根据坡度概念及梯形的高,可以求出 AE,DF 的长. (3)由矩形的性质可得 EF 与 BC 的数量关系,求出 EF 的长,从而求出底 AD 的长. - 5 - (4)在 RtΔABE 中,由坡角和坡度之间的关系可求出坡角. 【师生活动】 教师引导学生分析,然后学生独立完成解答过程,小组内交流答案,小组 代表板书过程,教师进行点评. 【课件展示】 解:如图所示,作 BE⊥AD,CF⊥AD,垂足分别为 E,F. 在四边形 BEFC 中, ∵BC∥AD,∠AEB=∠DFC=90°, ∴四边形 BEFC 为矩形. ∴BC=EF,BE=CF. 在 RtΔABE 和 RtΔDCF 中, ∵∠A=∠D,∠AEB=∠DFC,BE=CF, ∴RtΔABE≌RtΔDCF. ∴AE=DF. 在 RtΔABE 中, tan α= = 1 1 . 25 = 4 5 ,BE=4, ∴α≈38°39',AE=5. ∴AD=AE+EF+FD=BC+2AE=10+2×5=20. 即路基下底的宽为 20 m,坡角约为 38°39'. 追问: 你能总结利用解直角三角形的有关知识解决实际问题的一般过程吗? 【师生活动】 学生思考后小组合作交流,共同归纳解题过程,教师对学生的回答给予鼓 励,师生共同归纳解题思路和方法. 归纳: (1)将实际问题抽象成数学问题(画出示意图,将其转化为解直角三角形的问题); (2)根据问题中的条件,适当选用锐角三角函数解直角三角形; (3)得到数学问题的答案; (4)得到实际问题的答案. [设计意图] 学生在教师的引导下,通过独立思考和小组合作交流,利用解直角三角形 的知识解决有关坡度问题,进一步让学生体会将实际问题转化为数学问题的建模过程.坡度 问题计算过程很繁琐,通过严格要求学生,选择最简练、准确的方法计算,培养学生运算能力, 提高学生的数学思维及解题能力. 做一做 【课件展示】 如图所示,某水库大坝的横断面是四边形 ABCD,DC∥AB,坝顶宽 CD=3 m, - 6 - 斜坡 AD=16 m,坝高为 8 m,斜坡 BC 的坡度为 1 3 .求斜坡 AD 的坡角α和坝底的宽 AB(结果精确 到 0.01 m). 【师生活动】 学生独立完成后,小组内交流答案,教师在巡视过程中帮助有困难的学生, 对学生的展示进行点评,同时规范学生的书写过程. [设计意图] 通过做一做,使学生进一步体会运用解直角三角形知识解决坡度问题的过 程,培养学生建模思想及将实际问题转化为数学问题的能力,提高学生分析问题、解决问题的 能力. [知识拓展] 1.解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形求解. 2.坡度也叫坡比,即 i= ,一般写成 1∶m 的形式(比的前项是 1,后项可以是整数,也可以 是小数或根式). 3.坡度 i 与坡角α之间的关系为 i=tan α. 4.坡角越大,坡度越大,坡面越陡. 三、课堂小结： 解直角三角形的有关知识解决实际问题的一般过程: (1)将实际问题抽象成数学问题(画出示意图,将其转化为解直角三角形的问题); (2)根据问题中的条件,适当选用锐角三角函数解直角三角形; (3)得到数学问题的答案; (4)得到实际问题的答案.