- 2021-04-28 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011高考数学专题复习:《算法与程序框图》专题训练一
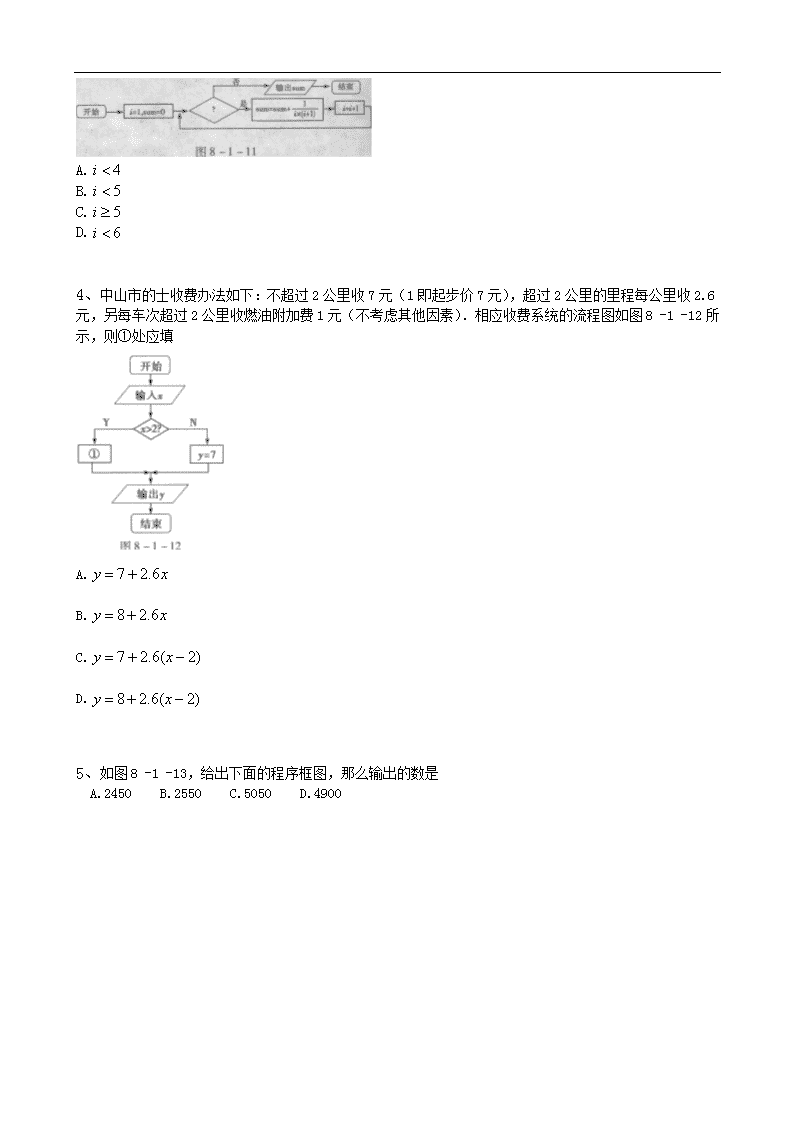
2011《算法与程序框图》专题训练一 一、选择题 1、阅读如图8 -1 -18所示的程序框图,运行相应的程序,输出的结果是 A.-1 B. C.2 D.O 2、某流程图如图8-1-5所示,现输入如下四个函数,则可以输出的函数是 3、一个算法的程序框图如图8-1 -11所示,若该程序输出的结果为,则判断框中应填入的条件是 A. B. C. D. 4、中山市的士收费办法如下:不超过2公里收7元(1即起步价7元),超过2公里的里程每公里收2.6元,另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的流程图如图8 -1 -12所示,则①处应填 A. B. C. D. 5、如图8 -1 -13,给出下面的程序框图,那么输出的数是 A.2450 B.2550 C.5050 D.4900 6、若某程序框图如图8-1 -14所示,则该程序运行后输出的B等于 A.7 B.15 C.31 D.63 7、如图8-1 -15所示的算法流程图中.第3个输出的数是 A.1 B. C.2 D. 8、程序框图如图8 -1 -17: 如果上述程序运行的结果为S=132,那么判断框中应填入 A.≤10? B.≥10? C.≤ll? D.≥11? 9、已知程序框图如图8 -1 - 24所示,则该程序框图的功能是“求数列的前10项和”,则判断框内应填写 10、为调查深圳市中学生平均每人每天参加体育锻炼时间(单位:分钟),按锻炼时间分下列4种情况统计:①0-10分钟;②11-20分钟;③21-30分钟;④30分钟以上.有10 000名中学生参加了此项调查活动,如图8 -1 - 25是此次调查中某一项的流程图,其输出的结果是6 200.则平均每天参加体育锻炼时间在O-20分钟内的学生的频率是 A.3 800 B.6 200 C.0.38 D.0.62 11、如图8-1 -16中的程序框图输出的结果为 A.2 B.3 C.1 D.O 二、填空题 12、一个算法的程序框图如图8 -1 -19所示,若该程序输出的结果为,则判断框中应填入的条件是____. 13、已知数列{}的各项均为正数,观察如图8 -1- 27所示的程序框图,若=5,=10时,分别有和,则数列{}的通项为=____. 14、图8-1 -20是一程序框图,则其输出的结果为_____________. 15、一个算法如下: 第一步:计算 第二步:若>0,输出最小值; 第三步:若<0,输出最大值. 已知.,,,则运行以上步骤输出的结果为____. 16、如图8-1 - 21所示程序框图,则其输出的结果S=_________. 17、按如图8-1 - 22所示程序框图来计算: 如果=5,应该运算__________次才停止. 18、运行如图8-1 - 23所示的程序流程图,则输出I的值为_________. 19、阅读如图8 -1 -10所示的程序框图,该程序输出的结果是______. 20、如图8-1 - 26给出了一个程序框图,其作用是输入的值,输出相应的的值,若要使输入的的值与输出的的值相等,则这样的值的集合为________. 以下是答案 一、选择题 1、C 解析:由算法程序图可知, 输出S=2.故选C. 2、D 解析:本题的程序框图的功能是判断函数是否是奇函数且是否存在零点.满足既是奇函数又存在零点的函数是选项D. 3、D 解析:当i=l,sum=O,满足条件执行+1 =2;满足条件执行 ;满足条件执行 ;满足条件执行 ;满足条件执行 ;不满足条件,结束循环输出,故判断框中应填入的条件是<6.选D. 4、D 解析:根据题意可知>2时,收费应为起步价7元+超过2公里的里程收费2.6(-2)元+燃油附加费1元=8+2.6(-2),故选D. 5、A 解析:由程序框图可知,此程序框图的功能是求和,即2+4+…+98=2 450.故选A. 6、 解析: 此时退出循环,输出B= 63.故选D. 7、 解析:,故选C. 8、A 解析: 根据程序框图,不满足条件执行S=Sxk=12,=12 -1= 11;不满足条件执行s =12×11= 132, =11 -1 =10;满足条件,输出S=132.故判断框中应填入≤10?,故选A. 9、B 解析:=l时, …… = 11时,结束循环,所以选B. 10、C 解析:由程序框图,当输人体育锻炼时间时,,计数,一直到>10 000,即10 000个数据全部输入完,故输出的结果6 200是每天参加体育锻炼时间的学生人数,则每天体育锻炼时间在0~20分钟内的学生人数是10 000 -6200=3 800,其频率为3 800÷10 000 = 0.38.故选c. 11、D 解析:1=1≤5.A +I=l除以5的余数是1;I= 1+1=2≤5,A +I=3除以5的余数是3;I:2+l=3≤5,A +I=6除以5的余数是1;I=3+l=4≤5.A +I=5除以5的余数是0;I=4 +1 =5≤5,A+I=5除以5的余数是0;I=5 +1 =6 >5,此时退出循环,故输出0. 二、填空题 12、? 解析:由循环体可知,当sum=1时,当 ,当sum =3时因此,判断框中应填:i<4?或sum<3?. 13、 解析:由框图可知 { }是等差数列,其公差为d,则有, 由题意可知,=5时, 解得 14、 解析: 15、2 解析:只要按照算法的含义有步骤地描述解决的过程,便可得到该题的结果,本题算法用于求二次函数的最值,故输出最小值2. 16、 解析: -l= 35,=8,满足条件,结束循环,故输出S=35. 17、4 解析:,所 以运算4次才停止. 18、7 解析:当累加变量I=7时,P=15 x7 =105 >100,输出I=7. 19、729 解析:由程序框图可知,输入初始值 4,此时停止循环,故输出的结果是729. 20、{0,1,3}解析:依题意得,或 =l,或 =3.查看更多