- 2021-04-28 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学第二章 相交线与平行线 周周测4(2-3) 北师大版
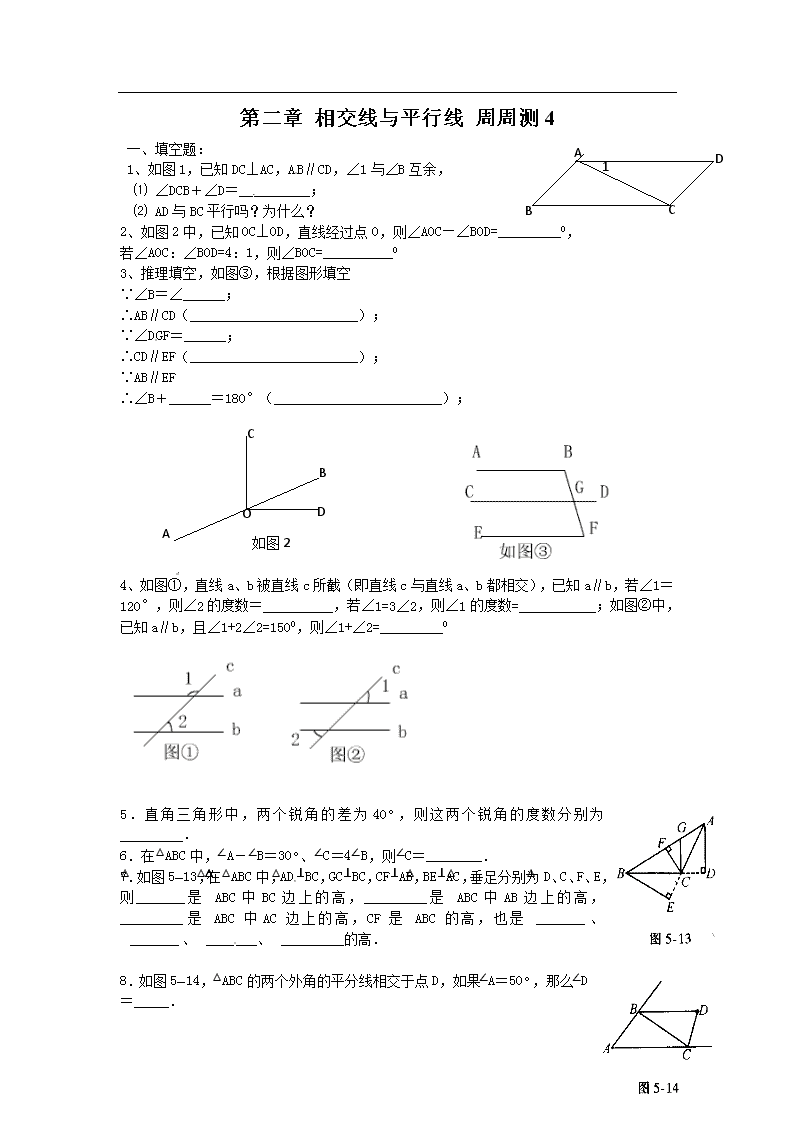
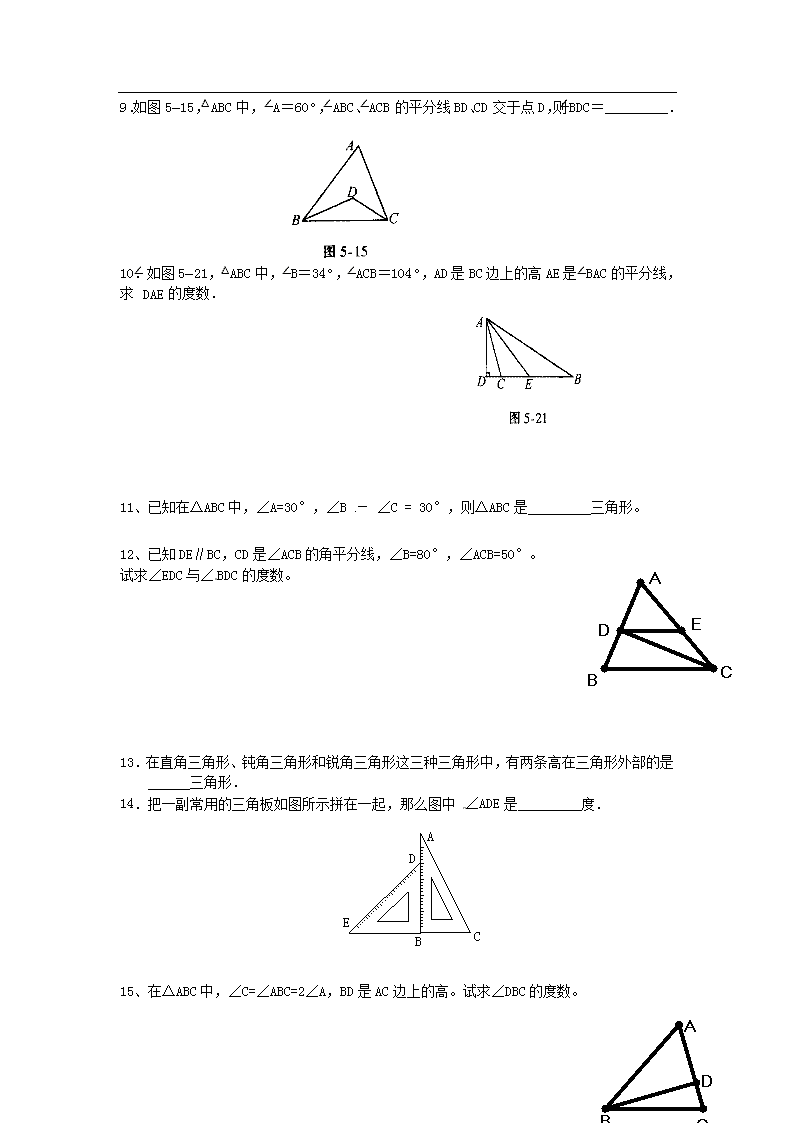
第二章 相交线与平行线 周周测4 A B C D 1 一、填空题: 1、如图1,已知DC⊥AC,AB∥CD,∠1与∠B互余, ⑴ ∠DCB+∠D=__________;[来源:学.科.网] ⑵ AD与BC平行吗?为什么? 2、如图2中,已知OC⊥OD,直线经过点O,则∠AOC—∠BOD=_________0, 若∠AOC:∠BOD=4:1,则∠BOC=__________0 3、推理填空,如图③,根据图形填空 ∵∠B=∠______; ∴AB∥CD(________________________); ∵∠DGF=______; ∴CD∥EF(________________________); ∵AB∥EF ∴∠B+______=180°(________________________); O C D B A 如图2 4、如图①,直线a、b被直线c所截(即直线c与直线a、b都相交),已知a∥b,若∠1=120°,则∠2的度数=__________,若∠1=3∠2,则∠1的度数=___________;如图②中, 已知a∥b,且∠1+2∠2=1500,则∠1+∠2=_________0 5.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________. 6.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________. 7.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是△ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高. 8.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____. 9.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_________. [来源:学科网] 10.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高AE是∠BAC的平分线,求∠DAE的度数. 11、已知在△ABC中,∠A=30°,∠B - ∠C = 30°,则△ABC是 三角形。 12、已知DE∥BC,CD是∠ACB的角平分线,∠B=80°,∠ACB=50°。 A B C D E 试求∠EDC与∠BDC的度数。 [来源:Zxxk.Com] 13.在直角三角形、钝角三角形和锐角三角形这三种三角形中,有两条高在三角形外部的是 ______三角形. 14.把一副常用的三角板如图所示拼在一起,那么图中 ∠ADE是 度. 15、在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高。试求∠DBC的度数。 A B C D 16、如图,已知DE//BC,BE平分∠ABC,∠C=55°,∠ABC=70°,求∠BED与∠BEC的度数。 A B C D E [来源:学&科&网Z&X&X&K] 第二章 相交线与平行线 周周测3参考答案与解析 1. 解(1)∠DCB+∠D=180° (2)AD与BC平行. 因为AB∥CD,DC⊥AC,得∠BAC是直角,∠BAC=90; ∠1与∠B互余,即∠1+∠B=90; 所以∠1+∠B+∠BAC=∠B+∠BAD=180 根据"同旁内角互补,两直线平行",得AD与BC平行. 2. 90° 3. ∠BGD 内错角相等,两直线平行 ∠F 内错角相等,两直线平行 ∠F 两直线平行,同旁内角互补 4.60° 135° 100° 5.65° 25° 6. 100° 7. AD CF BE BCG ACG CGF ACF 8. 65° 9.120° 10.解:∵∠B=34°,∠ACB=104°,∴∠CAB=42°. ∵AE是∠CAB的平分线,∴∠CAE=∠BAE=21°. ∵AD是△ABC边BC上的高,∴∠ADB=90° ∴∠DAB=90°-∠B=56° ∴∠DAE=∠DAB-∠EAB=56°-21°=35°. 11. 直角 12. 解:∵CD是∠ACB的角平分线,∠ACB=50° ∴∠BCD=∠DCE=25° ∴∠BDC=180-∠B-∠BCD=180°-80°-25°=75° ∵DE∥BC,∴∠BCD=∠ECD=25°[来源:Zxxk.Com] 13. 钝角 14. 135° 15.解:∵∠C=∠ABC=2∠A,∠C+∠A+∠ABC=180° ∴2∠A+2∠A+∠A=180,∠A=36°,∠C=72° ∵BD是AC边上的高,∴∠BDC=90°, ∴∠CBD=90°-∠C=18° 16. ∵BE平分∠ABC,∠ABC=70°, ∴∠ABE=∠CBE=35° ∵DE∥BC, ∴∠CBE=∠DBE=35°,∠BEC=180°-∠C-∠CBE=180°-55°-35°=90°查看更多