九年级上册青岛版数学教案4-7一元二次方程的应用

九年级上册青岛版数学教案4-7一元二次方程的应用

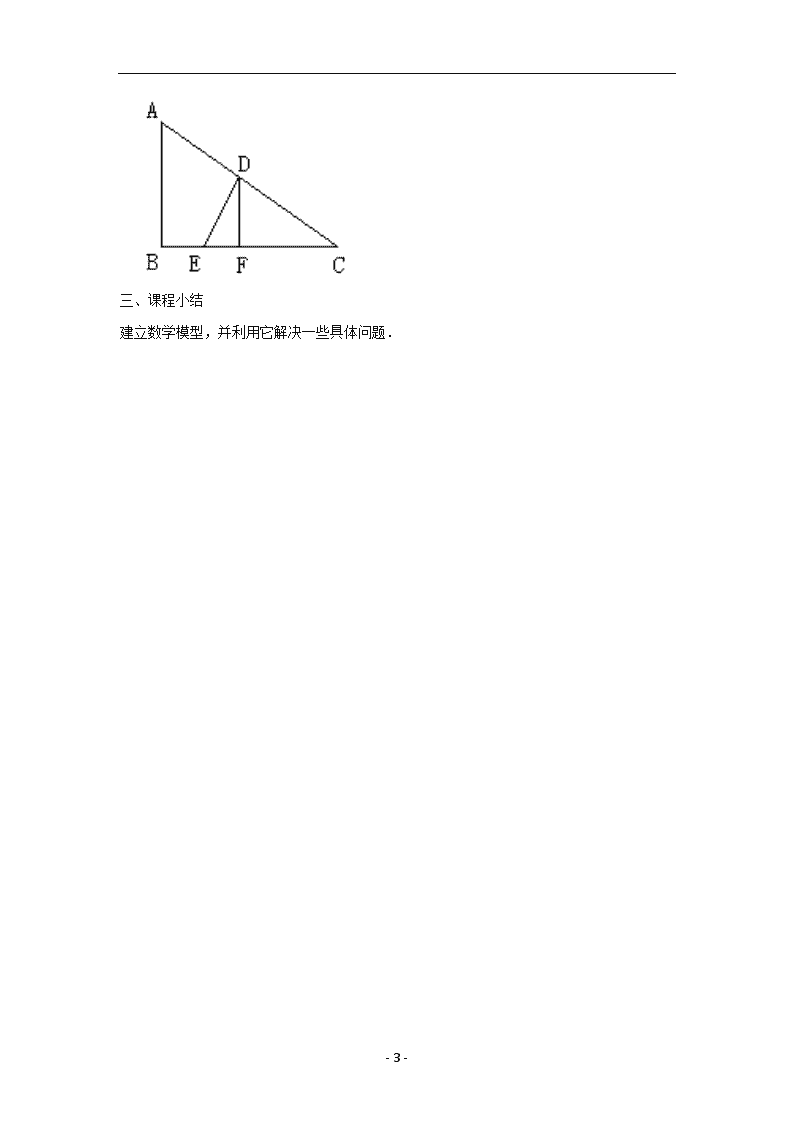
- 1 - 4.7 一元二次方程的应用 教学目标 【知识与能力】 1．能根据具体问题中的数量关系，列出一元二次方程，体会方程是刻画现实世界的一个有 效的数学模型． 2．能根据具体问题的实际意义，检验结果是否合理． 【过程与方法】 经历将实际问题抽象为代数问题的过程，探索问题中的数量关系，并能运用一元二次方程对 之进行描述． 【情感态度价值观】 通过用一元二次方程解决身边的问题，体会数学知识应用的价值，提高学生学习数学的兴趣， 了解数学对促进社会进步和发展人类理性精神的作用． 教学重难点 【教学重点】 列一元二次方程解有关问题的应用题． 【教学难点】 发现问题中的等量关系． 课前准备 无 教学过程 一、复习引入 我们已经知道，生产、生活中的一些实际问题，有时可以利用一元二次方程来描述其中已知 量与未知量之间的相等关系，运用一元二次方程的有关知识，常常可以使这些实际问题得到 解决. 【思考】 列方程解应用题的基本步骤有哪些？应注意什么？ 二、探索新知 【问题情境】 练习：某林场计划修一条长750m，断面为等腰梯形的渠道，断面面积为1.6m2，上口宽比渠 深多2m，渠底比渠深多0.4m． (1)渠道的上口宽与渠底宽各是多少？ (2)如果计划每天挖土48m3，需要多少天才能把这条渠道挖完？ 分析：因为渠深最小，为了便于计算，不妨设渠深为xm，则上口宽为x+2，渠底为x+0.4，那 么，根据梯形的面积公式便可建模． 解：(1)设渠深为xm 则渠底为(x+0.4)m，上口宽为(x+2)m 依题意，得： 1 2 (x+2+x+0.4)x=1.6 - 2 - 整理，得：5x2+6x-8=0 解得：x1= 4 5 =0.8m，x2=-2(舍) ∴上口宽为2.8m，渠底为1.2m． (2)1.6 750 48  =25天 答：渠道的上口宽与渠底深各是2.8m和1.2m；需要25天才能挖完渠道． 练习：某商场礼品柜台春节期间购进大量贺年卡，一种贺年卡平均每天可售出500张，每张 盈利0.3元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，如果这种贺年 卡的售价每降低0.1元，那么商场平均每天可多售出100张，商场要想平均每天盈利120元， 每张贺年卡应降价多少元？ 老师点评：总利润=每件平均利润×总件数．设每张贺年卡应降价x元，则每件平均利润应是 (0.3-x)元，总件数应是(500+ 0.1 x ×100) 解：设每张贺年卡应降价x元 则(0.3-x)(500+100 0.1 x )=120 解得：x=0.1 答：每张贺年卡应降价0.1元． 学生活动：合作交流，讨论解答． 例1：将一根长为64的铁丝剪成两段，再将每段分别围成正方形（课本第150页图4-2），如果 两个正方形的面积的和等于160cm2，求两个正方形的边长. 例2：新华商场销售某种冰箱，每台进货价为2500元，市场调研表明：当销售价为2900元时， 平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台．商场要想使这种 冰箱的销售利润平均每天达到5000元，那么这种冰箱的定价应是多少？ 例3：机动车尾气污染是导致城市空气质量恶化的重要原因.为解决这一问题，某市试验将现 有部分汽车改装成液化石油气燃料汽车(成为环保汽车).按计划该市今后两年内将使全市的 这种环保汽车由目前的100辆增加到196辆，求这种环保汽车平均每年增长的百分率. 例4：如图，某海军基地位于A处，在其正南方向200海里处有一重要目标B，在B的正东方向2 00海里处有一重要目标C，小岛D位于AC的中点，岛上有一补给码头：小岛F位于BC上且恰好 处于小岛D的正南方向，一艘军舰从A出发，经B到C匀速巡航，一般补给船同时从D出发，沿 南偏西方向匀速直线航行，欲将一批物品送达军舰．(1)小岛D和小岛F相距多少海里？ (2)已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇于E处，那么相遇时 补给船航行了多少海里？(结果精确到0.1海里) - 3 - 三、课程小结 建立数学模型，并利用它解决一些具体问题．