- 2021-02-26 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
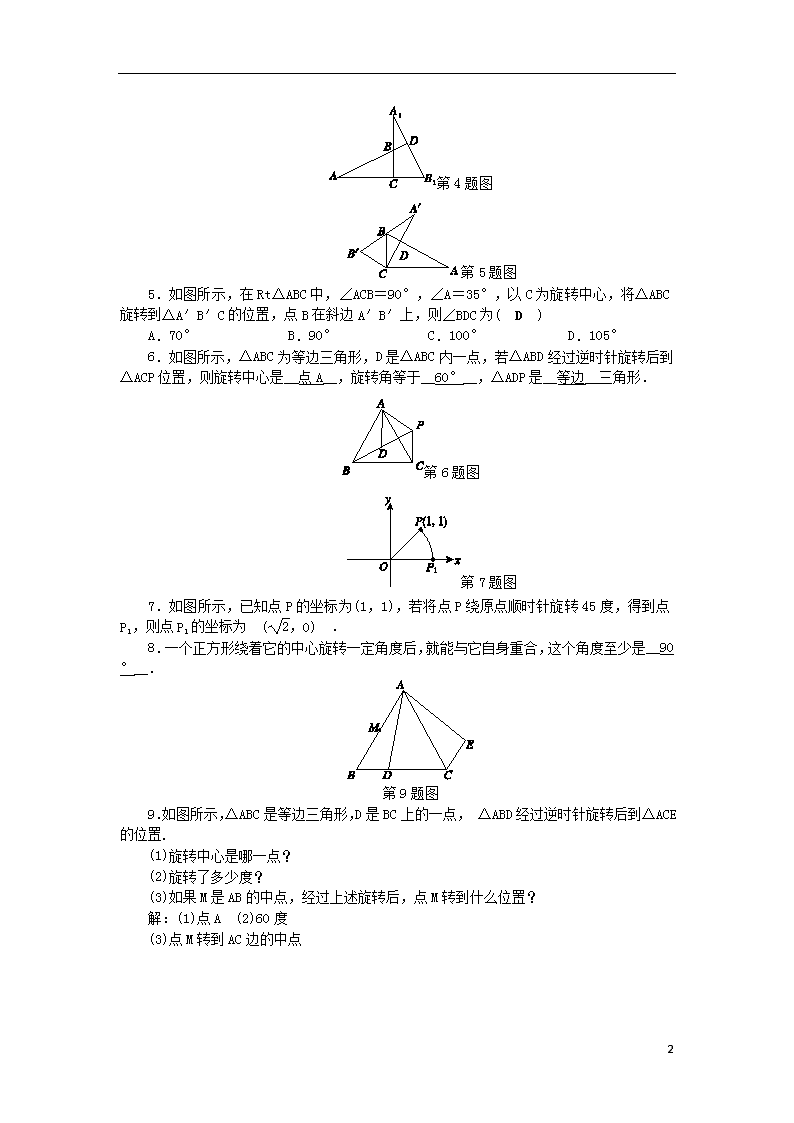
2020九年级数学上册 第3章 圆的基本性质 3
3.2 图形的旋转 (见A本23页) A 练就好基础 基础达标 1.下列现象中属于旋转的是( C ) A.电梯的升降运动 B.飞机起飞后冲向空中的过程 C.汽车方向盘的转动 D.笔直的铁轨上飞驰而过的火车 2.如图所示,△ABC按顺时针方向旋转一个角度后得△A′B′C′,图中的旋转中心是( A ) A.A点 B.B点 C.C点 D.B′点 第2题图 第3题图 3.如图所示,图中的每个阴影旋转一个角度后,能互相重合,这个角度可以是( C ) A.30° B.45° C.120° D.90° 4.如图所示,直角三角形ABC绕直角顶点C顺时针方向旋转90°后到达△A1B1C,延长AB交A1B1于点D,则∠ADA1的度数是( D ) A.30° B.60° C.75° D.90° 6 第4题图 第5题图 5.如图所示,在Rt△ABC中,∠ACB=90°,∠A=35°,以C为旋转中心,将△ABC旋转到△A′B′C的位置,点B在斜边A′B′上,则∠BDC为( D ) A.70° B.90° C.100° D.105° 6.如图所示,△ABC为等边三角形,D是△ABC内一点,若△ABD经过逆时针旋转后到△ACP位置,则旋转中心是__点A__,旋转角等于__60°__,△ADP是__等边__三角形. 第6题图 第7题图 7.如图所示,已知点P的坐标为(1,1),若将点P绕原点顺时针旋转45度,得到点P1,则点P1的坐标为 (,0) . 8.一个正方形绕着它的中心旋转一定角度后,就能与它自身重合,这个角度至少是__90°__. 第9题图 9.如图所示,△ABC是等边三角形,D是BC上的一点, △ABD经过逆时针旋转后到△ACE的位置. (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,经过上述旋转后,点M转到什么位置? 解:(1)点A (2)60度 (3)点M转到AC边的中点 6 第10题图 10.如图所示,在正方形ABCD中作∠EAF=45°,分别交边BC,CD于点E,F(不与顶点重合),把△ABE绕点A逆时针旋转90°落在△ADG的位置. (1)请你在图中画出△ADG(不写作法); (2)试说明BE,DF与EF之间的数量关系. 第10题答图 解:(1)作图如图. (2)BE+DF=EF. 证明:∵△ADG≌△ABE, ∴AG=AE,∠DAG=∠BAE,DG=BE, 又∵∠EAF=45°, 即∠DAF+∠BAE=∠EAF=45°, ∴∠GAF=∠FAE, ∵在△GAF和△FAE中, AG=AE,∠GAF=∠FAE,AF=AF, ∴△AFG≌△AFE(SAS).∴GF=EF. 又∵DG=BE,∴GF=BE+DF, ∴BE+DF=EF. B 更上一层楼 能力提升 11.在图形旋转中,下列说法错误的是( C ) A.图形上各点的旋转角度相同 B.对应点到旋转中心距离相等 C.由旋转得到的图形也一定可以由平移得到 D.旋转不改变图形的大小、形状 第12题图 12.2017·河南中考我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O.固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( D ) A.(,1) B.(2,1) C.(1,) D.(2,) 6 第13题图 13.如图所示,将直角三角形ABC绕直角顶点C顺时针旋转90°,得到△A′B′C.连结AA′,若∠1=20°,则∠B的度数是__65°__. 第14题图 14.金华中考在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F. (1)若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E,F的坐标; (2)当点F落在x轴上方时,试写出一个符合条件的点B的坐标. 解:(1)作图如图,∵△AOB绕点A逆时针旋转90°后得到△AEF, 第14题答图 ∴AO⊥AE,AB⊥AF,BO⊥EF,AO=AE,AB=AF. ∵EF=OB=4, ∴点E的坐标是(3,3),点F的坐标是(3,-1). (2)∵点F落在x轴的上方, ∴EF<AO,BO=EF, ∵AO⊥AE,AO=AE, ∴点E的坐标是(3,3). 又∵EF=OB, ∴OB<AO,AO=3,∴OB<3, ∴一个符合条件的点B的坐标是(-2,0). 第15题图 6 15.2017·徐州中考如图所示,已知AC⊥BC,垂足为C,AC=4,BC=3,将线段AC绕点A按逆时针方向旋转60°得到线段AD,连结DC,DB. (1)线段DC=__4__; (2)求线段DB的长度. 解:(1)证△ACD是等边三角形,得CD=4. 第15题答图 (2)作DE⊥BC于点E. ∵△ACD是等边三角形, ∴∠ACD=60°, 又∵AC⊥BC, ∴∠DCE=∠ACB-∠ACD=90°-60°=30°, ∴Rt△CDE中,DE=DC=2, CE=DC·cos30°=4×=2, ∴BE=BC-CE=3-2=. ∴在Rt△BDE中,BD===. C 开拓新思路 拓展创新 16.如图所示,将△ABC绕点B逆时针旋转α得到△DBE,点E在AB边上,DE的延长线与AC相交于点F,连结DA,BF,∠ABC=α=60°,BF=AF. (1)求证:DA∥BC. (2)猜想线段DF,AF的数量关系,并证明你的猜想. 第16题图 解:(1)证明:由旋转的性质可知:∠DBE=∠ABC=60°,BD=AB, ∴△ABD为等边三角形, ∴∠DAB=60°, ∴∠DAB=∠ABC, ∴DA∥BC. 第16题答图 (2)猜想:DF=2AF, 6 证明如下:如图,在DF上截取DG=AF,连结BG, 由旋转的性质可知,DB=AB,∠BDG=∠BAF, 在△DBG和△ABF中, ∴△DBG≌△ABF(SAS), ∴BG=BF,∠DBG=∠ABF, ∵∠DBG+∠GBE=α=60°, ∴∠GBE+∠ABF=60°,即∠GBF=α=60°, 又∵BG=BF, ∴△BGF为等边三角形, ∴GF=BF, 又∵BF=AF, ∴FG=AF, ∴DF=DG+FG=AF+AF=2AF. 6查看更多