【数学】2019届一轮复习北师大版　任意角和弧度制及任意角的三角函数学案

【数学】2019届一轮复习北师大版　任意角和弧度制及任意角的三角函数学案

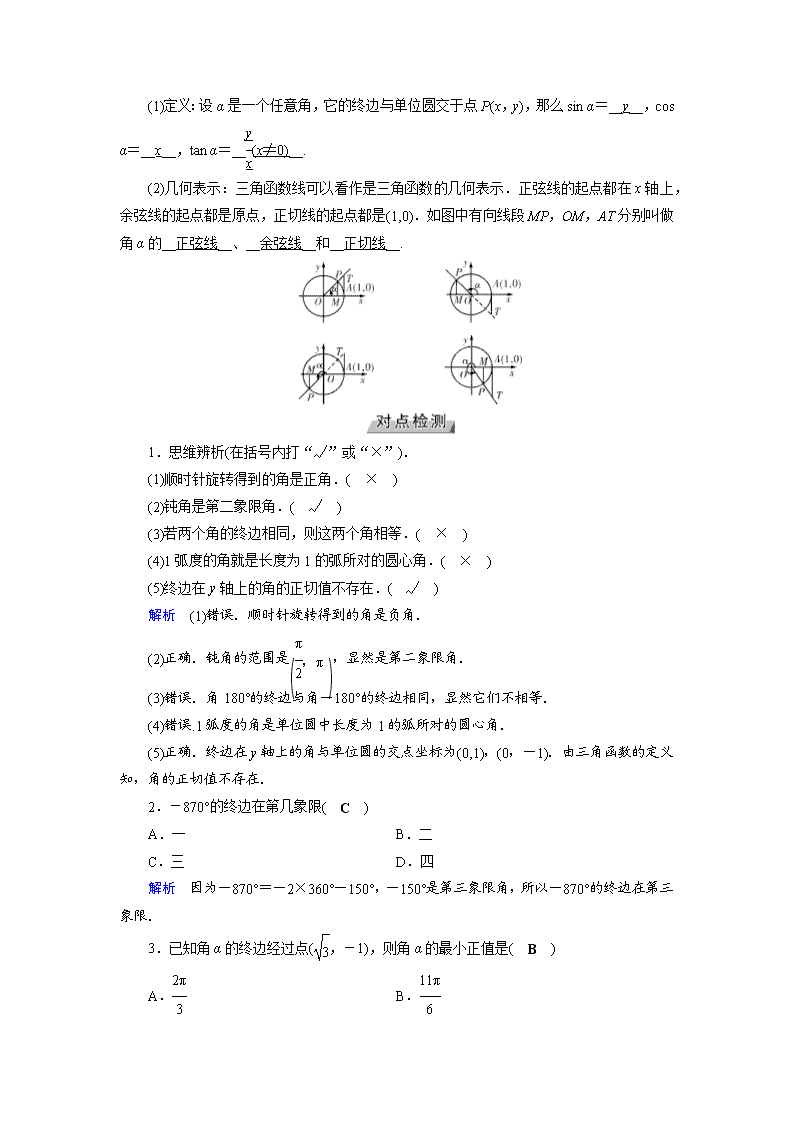
第三章　三角函数、解三角形 第17讲　任意角和弧度制及任意角的三角函数 考纲要求 考情分析 命题趋势 ‎1.了解任意角和弧度制的概念．‎ ‎2．能进行弧度与角度的互化．‎ ‎3．理解任意角三角函数的定义.‎ ‎2017·北京卷，9‎ ‎2016·四川卷，11‎ ‎2015·福建卷，6‎ ‎1.根据角的终边上的点的坐标求三角函数值．‎ ‎2．根据三角函数值求参数值．‎ ‎3．利用三角函数的定义判断三角函数的图象.‎ 分值：5分 ‎1．角的有关概念 ‎(1)角的形成：角可以看成平面内__一条射线__绕着端点从一个位置旋转到另一个位置所成的__图形__.‎ ‎(2)从运动的角度看，角可分为正角、__负角__和__零角__.‎ ‎(3)从终边位置来看，角可分为象限角与轴线角．‎ ‎(4)若β与α是终边相同的角，则β用α表示为__β＝2kπ＋α，k∈Z__.‎ ‎2．弧度制 ‎(1)定义：长度等于__半径__的弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度．‎ ‎(2)角α的弧度数：如果半径为r的圆的圆心角α所对弧的长为l，那么角α的弧度数的绝对值是|α|＝____.‎ ‎(3)角度与弧度的换算：1°＝____rad,1 rad＝__°__.‎ ‎(4)弧长、扇形面积的公式：设扇形的弧长为l，圆心角大小为α rad，半径为r，则l＝__|α|r__，扇形的面积为S＝lr＝__|α|·r2__.‎ ‎3．任意角的三角函数 ‎(1)定义：设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么sin α＝__y__，cos ‎ α＝__x__，tan α＝__(x≠0)__.‎ ‎(2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP，OM，AT分别叫做角α的__正弦线__、__余弦线__和__正切线__.‎ ‎1．思维辨析(在括号内打“√”或“×”)．‎ ‎(1)顺时针旋转得到的角是正角．(　×　)‎ ‎(2)钝角是第二象限角．(　√　)‎ ‎(3)若两个角的终边相同，则这两个角相等．(　×　)‎ ‎(4)1弧度的角就是长度为1的弧所对的圆心角．(　×　)‎ ‎(5)终边在y轴上的角的正切值不存在．(　√　)‎ 解析　(1)错误．顺时针旋转得到的角是负角．‎ ‎(2)正确．钝角的范围是，显然是第二象限角．‎ ‎(3)错误．角180°的终边与角－180°的终边相同，显然它们不相等．‎ ‎(4)错误.1弧度的角是单位圆中长度为1的弧所对的圆心角．‎ ‎(5)正确．终边在y轴上的角与单位圆的交点坐标为(0,1)，(0，－1)．由三角函数的定义知，角的正切值不存在．‎ ‎2．－870°的终边在第几象限(　C　)‎ A．一　　　 B．二　　　　‎ C．三　　　 D．四 解析　因为－870°＝－2×360°－150°，－150°是第三象限角，所以－870°的终边在第三象限．‎ ‎3．已知角α的终边经过点(，－1)，则角α的最小正值是(　B　)‎ A．　　　 B．　　　　‎ C．　　　 D． 解析　∵sin α＝＝－，且α的终边在第四象限，∴α的最小正值为π.‎ ‎4．若sin α<0且tan α>0，则α是(　C　)‎ A．第一象限角　　　 B．第二象限角 C．第三象限角　　　 D．第四象限角 解析　由sin α<0，知α在第三或第四象限或α终边在y轴的负半轴上，由tan α>0，知α在第一或第三象限，因此α在第三象限．‎ ‎5．弧长为3π，圆心角为135°的扇形半径为__4__，面积为__6π__.‎ 解析　弧长l＝3π，圆心角α＝π，由弧长公式l＝|α|·r，得r＝＝＝4，面积S＝lr＝6π.‎ 一　角及其表示 ‎(1)若要确定一个绝对值较大的角所在的象限，一般是先将角化为2kπ＋α(0≤α<2π)(k∈Z)的形式，然后再根据α所在的象限予以判断．‎ ‎(2)利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k赋值来求得所需角．‎ ‎【例1】 (1)写出终边在直线y＝x上的角的集合．‎ ‎(2)若角θ的终边与π角的终边相同，求在[0,2π]内终边与角的终边相同的角．‎ ‎(3)已知角α是第一象限角，试确定2α，所在的象限．‎ 解析　(1)终边在直线y＝x上的角的集合为.‎ ‎(2)与角终边相同的角的集合是，∴所有与角终边相同的角可表示为＝π＋kπ，k∈Z.∴在[0,2π]内终边与角终边相同的角有π，π，π.‎ ‎(3)∵2kπ<α<2kπ＋，k∈Z，‎ ‎∴4kπ<2α<4kπ＋π，kπ<0，∴＝，即m＝.‎ 三　扇形的弧长及面积公式的应用 ‎(1)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．‎ ‎(2)求扇形面积的最大值时，常转化为二次函数的最值问题，利用配方法使问题得到解决．‎ ‎(3)在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形．‎ ‎【例3】 已知扇形的圆心角是α，半径为R，弧长为l.‎ ‎(1)若α＝60°，R＝‎10 cm，求扇形的弧长l；‎ ‎(2)若扇形的周长为‎20 cm，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？‎ ‎(3)若α＝，R＝‎2 cm，求扇形的弧所在的弓形的面积．‎ 解析　(1)l＝10×＝(cm)．‎ ‎(2)由已知得l＋2R＝20，‎ 所以S＝lR＝(20－2R)R＝10R－R2＝－(R－5)2＋25，所以R＝5时，S取得最大值25，此时l＝‎10 cm，α＝2 rad.‎ ‎(3)设弓形面积为S弓，由题知l＝ cm，‎ S弓＝S扇－S△＝××2－×22×sin＝－(cm2)．‎ ‎1．若sin α·tan α<0，且<0，则角α是(　C　)‎ A．第一象限角　　　 B．第二象限角 C．第三象限角　　　 D．第四象限角 解析　由sin α·tan α<0可知sin α，tan α异号，从而α为第二或第三象限角；由<0，可知cos α，tan α异号，从而α为第三或第四象限角．综上，α为第三象限角．‎ ‎2．sin 2·cos 3·tan 4的值(　A　)‎ A．小于0　　　 B．大于‎0　‎　　‎ C．等于0　　　 D．不存在 解析　∵sin 2>0，cos 3<0，tan 4>0，∴sin 2·cos 3·tan 4<0.‎ ‎3．若cos α＝－，且角α的终边经过点P(x,2)，则点P的横坐标x是(　D　)‎ A．2　　　 B．±2 C．－2　　　 D．－2 解析　r＝，由题意得＝－，解得x＝－2.‎ ‎4．已知半径为10的圆O中，弦AB的长为10.‎ ‎(1)求弦AB所对的圆心角α的大小；‎ ‎(2)求α所在的扇形弧长l及弧所在的弓形的面积S.‎ 解析　(1)在△AOB中，AB＝OA＝OB＝10，‎ ‎∴△AOB为等边三角形．∴弦AB所对的圆心角α＝.‎ ‎(2)由扇形的弧长与扇形面积公式，得l＝α·R＝×10＝，‎ S扇形＝R·l＝α·R2＝.‎ 又S△AOB＝OA·OB·sin＝25.‎ ‎∴弓形的面积S＝S扇形－S△AOB＝50.‎ 错因分析：用三角函数的定义求三角函数值时，不注意点的位置或对字母正负的讨论．‎ ‎【例1】 已知α角的终边过点P(‎3a，－‎4a)(a≠0)，求α角的三个三角函数值．‎ 解析　 根据任意角的三角函数的定义知 r＝＝＝5|a|.‎ 当a<0时，r＝－‎5a，sin α＝＝，cos α＝＝－，‎ tan α＝＝－；‎ 当a>0时，r＝‎5a，sin α＝＝－，cos α＝＝，‎ tan α＝＝－.‎ ‎【跟踪训练1】 已知角θ的终边上有一点P(x，－1)(x≠0)，且tan θ＝－x，求sin θ，cos θ.‎ 解析　∵θ的终边过点(x，－1)，∴tan θ＝－，‎ 又∵tan θ＝－x，∴x2＝1，∴x＝±1.‎ 当x＝1时，sin θ＝－，cos θ＝；‎ 当x＝－1时，sin θ＝－，cos θ＝－.‎ 课时达标　第17讲 ‎[解密考纲]本考点主要考查任意角、弧度制和三角函数的概念．‎ 通常以选择题、填空题的形式呈现，安排在比较靠前的位置．‎ 一、选择题 ‎1．将表的分针拨快10分钟，则分针旋转过程中形成的角的弧度数是(　C　)‎ A．　　 B． C．－　　 D．－ 解析　将表的分针拨快应按顺时针方向旋转，为负角，故A，B项不正确．又因为拨快10分钟，故应转过的角为圆周的，即为－×2π＝－.故选C．‎ ‎2．点P从(1,0)出发，沿单位圆逆时针方向运动弧长到达点Q，则点Q的坐标为(　A　)‎ A．　　 B． C．　　 D． 解析　由三角函数定义可知点Q的坐标(x，y)满足x＝cos＝－，y＝sin＝.‎ ‎3．已知角α的终边经过点(‎3a－9，a＋2)，且cos α≤0，sin α>0，则实数a的取值范围是(　A　)‎ A．(－2,3]　　 B．(－2,3)‎ C．[－2,3)　　 D．[－2,3]‎ 解析　由cos α≤0，sin α>0可知，角α的终边在第二象限或y轴的正半轴上，所以有解得－20，sin θ＋cos θ<0，∴|sin θ|>|cos θ|，∴cos 2θ＝|cos θ|2－|sin θ|2<0，∴cos 2θ＝－.‎ ‎9．设角α是第三象限角，且＝－sin，则角是第__四__象限角．‎ 解析　由α是第三象限角，知2kπ＋π<α<2kπ＋(k∈Z)，kπ＋<0.‎ ‎(1)求α角的集合；‎ ‎(2)求的终边所在的象限；‎ ‎(3)试判断tansincos的符号．‎ 解析　(1)由sin α<0，知α的终边在第三、四象限或y轴的负半轴上；由tan α>0，知α的终边在第一、三象限，‎ 故α的终边在第三象限，其集合为α.‎ ‎(2)由(2k＋1)π<α<2kπ＋，k∈Z，‎ 得kπ＋<0，cos<0，‎ 所以tansincos取正号；‎ 当在第四象限时，tan<0，sin<0，cos>0，‎ 所以tansincos也取正号．‎ 综上所述，tansincos取正号．‎