人教版六年级上册数学第七单元扇形统计图PPT

人教版六年级上册数学第七单元扇形统计图PPT

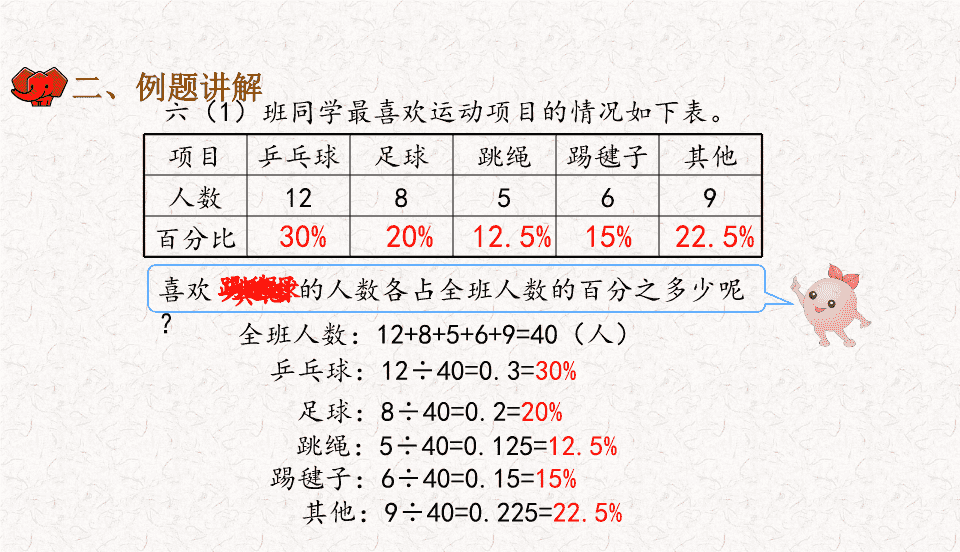
扇形统计图 7 人教版 · 六年级上册 第 1 课时 扇形统计图 一、新课引入 六（ 1 ）班的同学们在操场上进行着各种运动项目。 我觉得应该先调查一下喜欢每种运动的各有多少人。 学校要为我们班购置一些运动器材，你能提出一些建议吗？ 项目 乒乓球 足球 跳绳 踢毽子 其他 人数 12 8 5 6 9 百分比 六（ 1 ）班同学最喜欢运动项目的情况如下表。 全班人数： 12+8+5+6+9=40 （人） 二、例题讲解 喜欢 的人数各占全班人数的百分之多少呢？ 乒乓球 足球： 8 ÷ 40=0.2= 20% 跳绳： 5 ÷ 40=0.125= 12.5% 踢毽子： 6 ÷ 40=0.15= 15% 其他： 9 ÷ 40=0.225= 22.5% 乒乓球： 12 ÷ 40=0.3= 30% 足球 跳绳 踢毽子 其他 20% 12.5% 15% 22.5% 30% 项目 乒乓球 足球 跳绳 踢毽子 其他 人数 12 8 5 6 9 百分比 六（ 1 ）班同学最喜欢运动项目的情况如下表。 二、例题讲解 20% 12.5% 15% 22.5% 30% 根据统计表可以绘制什么统计图呢？ 可以绘制条形统计图。 乒乓球 足球 跳绳 踢毽子 其他 0 2 4 6 8 10 12 14 12 8 5 6 9 六（ 1 ）班最喜欢的运动项目统计图 还可以用 扇形统计图 来表示 各部分数量与总数之间的关系 。 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 12.5 15 20 22.5 项目 乒乓球 足球 跳绳 踢毽子 其他 人数 12 8 5 6 9 百分比 六（ 1 ）班同学最喜欢运动项目的情况如下表。 20% 12.5% 15% 22.5% 30% 二、例题讲解 六（ 1 ）班最喜欢的运动项目统计图 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 20 12.5 15 22.5 图中的整个圆表示什么？ 整个圆表示 全班的总人数。 喜欢踢毽的人数占总人数的百分之几？乒乓球的呢？ 喜欢踢毽的人数占总人数的 15% ，喜欢乒乓球的人数占总 人数的 30% 。 六（ 1 ）班最喜欢的运动项目统计图 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 20 12.5 15 22.5 各个扇形的大小与什么有关系？ 各个扇形的大小与班中喜欢 某项运动的人数占全班人数的百分之几 有关系。 用这样的统计图有什么好处？ 扇形统计图不仅可以直观地比较各个扇形的相对大小，还能清楚地表示出各部分与整体之间的关系。 六（ 1 ）班最喜欢的运动项目统计图 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 乒乓球 30 % 足球 ( )% 跳绳 ( )% 踢毽子 ( )% 其他 ( ) % 20 12.5 15 22.5 你还能提出什么数学问题吗？ 喜欢哪项运动的百分比最多？ 喜欢足球的比喜欢踢毽子的多百分之几？ 我们如何给六（ 1 ）班采购体育器材？ 二、例题讲解 （ 1 ）这两幅统计图有什么相同点和不同点？ （ 2 ）如果要你去采购体育器材，你会选择哪副图作参考？ 答：这两幅图都可以看出数量的多少，扇形统计图还能清楚地反映出喜欢每种运动项目的人数占总人数的百分之几。 乒乓球 30 % 足球 20 % 其他 22.5 % 踢毽 15 % 跳绳 12.5 % 六（ 1 ）班最喜欢的运动项目统计图 乒乓球 足球 跳绳 踢毽子 其他 0 2 4 6 8 10 12 14 12 8 5 6 9 六（ 1 ）班最喜欢的运动项目统计图 答：我会选择扇形统计图，因为根据扇形统计图我可以清楚的知道喜欢每项运动项目的人数占总人数的百分比，可以更好的分配每项应该买多少。 三、新知运用 1. 牛奶里含有丰富的营养成分，各种营养成分所占百分比如下。（ 教材 P97 做一做 ） 整个圆表示什么？ 整个圆表示一袋 250g 的牛奶。 87% 、 3.3% 、 4% 、 5% 、 0.7% 分别表示什么含义呢？ 87% 表示水分占牛奶的 87% ； 3.3% 表示蛋白质占牛奶的 3.3%... 三、新知运用 1. 牛奶里含有丰富的营养成分，各种营养成分所占百分比如下。 （ 教材 P97 做一做 ） 每天喝一袋 250g 的牛奶，能补充每种营养成分各多少克？ 水分： 250×87% ＝ 217.5 （ g ） 蛋白质： 250×3.3% ＝ 8.25 （ g ） 脂肪： 250×4% ＝ 10 （ g ） 乳糖： 250×5% ＝ 12.5 （ g ） 其他： 250×0.7% ＝ 1.75 （ g ） 答：一袋 250 g 的牛奶中，水分 217.5 克，蛋白质 8.25 克，脂肪 10 克，乳糖 12.5 克，其他 1.75 克。 三、新知运用 2. 陈东家每月各种支出计划如图所示。 （ 教材 P100 第 2 题 ） （ 1 ）你能得到那些数学信息？ 答：从扇形统计图中我知道陈东家每月还购房贷款和食品占总支出最多，水电占支出最少。 （ 2 ） 如果陈东家每月总计支出为 2000 元，你能提出并解决那些问题？ 陈东家每月教育花了多少钱？ 2000 × 15% ＝ 300 （元） 答：陈东家每月教育花了 300 元。 答案不唯一，还可以提出其他问题。 四、课堂小结 回顾本节课，你学会了什么？ 扇形统计图是用整个圆的面积 表示总数 , 用圆内的扇形面积表 示各部分占总数的百分比。 扇形统计图 它可以清楚地表示出各部 分数量与总数之间的关系 。 扇形统计图 部分数量与部分数 量之间的关系 。 扇形统计图 五、课后作业 完成课本“练习二十一”第 100 页第 1 题、第 101 页第 3 题、 第 4 题 。 扇形统计图 7 人教版 · 六年级上册 第 2 课时 选择合适统计图 乒乓球 30 % 足球 20% 跳绳 12.5% 踢毽子 15% 其他 22.5 % 六（ 1 ）班最喜欢的运动项目统计图 扇形统计图不仅可以直观地比较各个扇形的相对大小，还能清楚地表示出各部分与整体之间的关系。 一、新课引入 某地年降水量统计图 条形统计图能清楚地反映各个数量的多少 。 一、新课引入 第 27 － 30 届奥运会中国和美国获得金牌情况统计图 折线统计图不仅可以反映数量的多少，还能反映出数量增减变化趋势 。 一、新课引入 一、新课引入 名称 特点 条形统计图 能清楚地看出数量的多少 折线统计图 不仅可以反映数量的多少，还能看出 数量增减变化趋势 扇形统计图 不仅可以直观地比较各个扇形的相对大小 , 还 能 清楚地反映出各部分与整体的关系 三种统计图的特点如下： 二、例题讲解 下面几组数据分别选用哪种统计图表示更合适？ 年 份 2007 2008 2009 2010 2011 总量 / 棵 100 120 150 170 200 （ 1 ）绿荫小学 2007—2011 年校园内树木总量变化情况统计表。 树 种 杨树 柳树 松树 槐树 其他 百分比 /% 25 20 15 15 25 树 种 杨树 柳树 松树 槐树 其他 总量 / 棵 50 40 30 30 50 （ 2 ） 2011 年绿荫小学校园内各种树木所占百分比情况统计表。 （ 3 ） 2011 年绿荫小学校园内各种树木数量统计表。 二、例题讲解 年 份 2007 2008 2009 2010 2011 总量 / 棵 100 120 150 170 200 （ 1 ）绿荫小学 2007—2011 年校园内树木总量变化情况统计表。 2007 2008 2009 2010 2011 年份 总量 ／ 棵 0 50 100 150 200 250 100 120 150 170 200 绿荫小学 2007 － 2011 年校园内 树木总量变化情况统计图 条形统计图 给出了 5 年中每年的树木棵数。 用条形统计图和折线统计图都可以表示出数量的变化。 二、例题讲解 绿荫小学 2007 － 2011 年校园内 树木总量变化情况统计图 折线统计图 2007 2008 2009 2010 2011 0 50 100 150 200 250 100 120 150 170 200 年份 总量 ／ 棵 年 份 2007 2008 2009 2010 2011 总量 / 棵 100 120 150 170 200 （ 1 ）绿荫小学 2007—2011 年校园内树木总量变化情况统计表。 二、例题讲解 2007 2008 2009 2010 2011 年份 总量 ／ 棵 0 50 100 150 200 250 100 120 150 170 200 绿荫小学 2007 － 2011 年校园内 树木总量变化情况统计图 条形统计图 绿荫小学 2007 － 2011 年校园内 树木总量变化情况统计图 折线统计图 2007 2008 2009 2010 2011 0 50 100 150 200 250 100 120 150 170 200 总量 ／ 棵 年份 用条形统计图和折线统计图都可以表示出数量的变化。 折线统计图能更加直观地表示出数量随着时间的变化趋势 。 选择哪个统计图更合适呢？ 树 种 杨树 柳树 松树 槐树 其他 百分比 /% 25 20 15 15 25 （ 2 ） 2011 年绿荫小学校园内各种树木所占百分比情况统计表。 二、例题讲解 杨树 柳树 松树 槐树 其他 树种 百分比 0 5% 10% 15% 20% 25% 25% 20% 15% 15% 25% 绿荫小学校园内各种树木所占百分比情况统计图 条形统计图 给出了各种树木总量的百分比，用条形统计图和扇形统计图都可以表示出这些信息。 树 种 杨树 柳树 松树 槐树 其他 百分比 /% 25 20 15 15 25 （ 2 ） 2011 年绿荫小学校园内各种树木所占百分比情况统计表。 二、例题讲解 绿荫小学校园内各种树木所占百分比情况统计图 扇形统计图 二、例题讲解 选择哪个统计图更合适呢？ 用扇形统计图能更加直观地反映出部分与整体之间的关系。 绿荫小学校园内各种树木所占百分比情况统计图 扇形统计图 绿荫小学校园内各种树木所占百分比情况统计图 条形统计图 杨树 柳树 松树 槐树 其他 树种 百分比 0 5% 10% 15% 20% 25% 25% 20% 15% 15% 25% 树 种 杨树 柳树 松树 槐树 其他 总量 / 棵 50 40 30 30 50 （ 3 ） 2011 年绿荫小学校园内各种树木数量统计表。 二、例题讲解 杨树 柳树 松树 槐树 其他 树种 总量 / 棵 0 10 20 30 40 50 50 40 30 30 50 绿荫小学校园内各种树木数量统计图 条形统计图 给出了各种树木的数量，只能用条形统计图来表示。 树 种 杨树 柳树 松树 槐树 其他 总量 / 棵 50 40 30 30 50 （ 3 ） 2011 年绿荫小学校园内各种树木数量统计表。 二、例题讲解 杨树 柳树 松树 槐树 其他 树种 总量 / 棵 0 10 20 30 40 50 50 40 30 30 50 绿荫小学校园内各种树木数量统计图 条形统计图 为什么不用其他的统计图？ 由于各个树种处于平等、独立的地位，用折线统计图表示是不合适的，又因缺乏相应的百分比数据，所以也无法用扇形统计图表示。 三、新知运用 1. 在林业科学里，通常根据乔木生长期的长短将乔木分成不同的类型。下面是我国乔木林各龄组的面积构成情况。（ 教材 P99 做一做 ） 以上信息可以用什么统计图描述？哪种更直观些？ 答：这题可以用条形统计图和扇形统计图表示出这些信息，但用扇形统计图更能直观地看出它们之间的关系。 我是用 条形统计图 描述的。 33.82% 33.43% 14.82% 12.03% 5.9% 0.00% 5.00% 10.00% 15.00% 20.00% 25.00% 30.00% 35.00% 40.00% 幼龄林 中龄林 近熟林 成熟林 过熟林 我是用 扇形统计图 描述的。 幼龄林 33.82% 中龄林 33.43% 近龄林 14.82% 成龄林 12.03% 过龄林 5.9% 2. 截至 2012 年 6 月末，全国农村网民规模为 1.46 亿，比 2011 年 12 月末增加 1464 万。（教材 P103 第 7 题） （ 1 ）截至 2012 年 6 月末，我国共有网民多少人？ 146000000÷27.1% ≈ 538745387 （ 人 ） 答：我国共有网民约 538745387 人。 三、新知运用 （ 2 ） 2011 年 12 月末，我国共有农村网民多少人？ 146000000 － 14640000 ＝ 131360000 （人） 答：我国共有农村网民 131360000 人。 2. 截至 2012 年 6 月末，全国农村网民规模为 1.46 亿，比 2011 年 12 月末增加 1464 万。 （教材 P103 第 7 题） 三、新知运用 （3）请你把扇形统计图补充完整。 农村 城镇 27.1 72.9 2011 12 农村 城镇 2. 截至2012年6月末，全国农村网民规模为1.46亿，比2011年12月末增加1464万。（教材P103第7题） 三、新知运用 四、课堂小结 回顾本节课，你学会了什么？ 统计图 条形 折线 扇形 表示数量多少 表示数量增减变化 表示百分比 根据数据的特点进行选择 五、课后作业 完成课本“练习二十一”第 101 页第 5 题、第 104 页第 8 题。 节约用水 一 、情景导入 每个水龙头漏水的速度一样吗？ 每个水龙头漏水的速度不同。可以用（ 平均数 ）代表不同水龙头漏水的一般水平。 解决下面的问题 1. 以小组为单位，测量不同水龙头在一定时间内的漏水量，并制作出像下面这样的条形统计图。 5 小时 2. 平均每个水龙头一天漏水多少升 ?  一年呢 ? 一个漏水水龙头漏水情况统计表 一年浪费的水有： 72×365=26280 （ L ） 一天浪费的水有 72 升 可以装 3 桶多。 3. 学校有几个水龙头漏水 ? 全国大约有 30 万所学校用自来水，如果按照这个比率计算，全年大约要浪费多少吨水 ? 平均每吨水价为 2.5 元，一共要多支付多少水费 ? 如果 1 个人 1 年用 30t 水，这些水可供多少人用 1 年 ? 以 4 个水龙头为例： 26280L=26.28m 3 1×26.28=26.28 （吨） 26.28×4×300000=31536000 （吨） 平均每吨水价为 2.5 元，需要支付水费： 2.5×31536000=78840000 （元） 如果 1 个人 1 年用 30t 水，这些水可供多少人用 1 年？ 31536000÷30=1051200 （人） 看到这些触目惊心的数据，我们知道了在今后的生活中一定要做到节约用水，怎样才能做到呢 ? 随时关紧水龙头；所用水龙头都应该用节水型的；一水多用，洗脸水用后可以洗脚，然后冲厕所；刷牙时不要让水龙头一直开着；淘米水、煮过面条的水、用来洗碗筷，去油又节水；养鱼的水浇花，能促进花木生长 …… 二、 新知应用 小明刷牙时，不间断放水 30 秒，用水约 6 升。小刚用口杯接水刷牙，需要 3 口杯水，每杯用水约 0.2 升。 6÷ （ 0.2×3 ） =10 （次） （ 1 ）小明一次刷牙的用水量相当于小刚多少次刷牙的用水量？ （ 2 ）如果采用节水刷牙的方式，一个三口之家按每人每日刷牙两次算，那么每月 ( 按 30 天计算 ) 可节水多少升 ? 可以装 2 升的鲜橙多多少瓶 ? （ 6-0.6 ） ×2×3×30=972 （升） 972÷2=486 （瓶） 三、 课堂小结 水资源的浪费触目惊心，节约用水，人人有责。 通过这节课的学习你有什么收获？有不懂的问题请提出来。 四、 课后作业 练 习册中与本课时有关系的练习题。 　　 劳动，不仅仅意味着实际能力和技巧，而且首先意味着智力的发展，意味着思维和语言的修养。 —— 苏霍姆林斯基 扇形统计图 7 人教版 · 六 年级上册 单元 整理与复习 一、学习目标 3 .在独立思考的基础上加强交流，增强合作交流意识，培养良好的思维习惯和细心、认真的学习习惯，使得在学习中获得自信。 1. 进一步加深对条形统计图、折线统计图和扇形统计图的联系及区别的认识。 2. 通过练习，更清楚地认识扇形统计图可以直观地反映部分量占总量的百分比，提高从扇形统计图读出必要信息的能力，并能结合百分数进行准确的计算。 二、学习重难点 学习重点： 学习难点: 1. 从扇形统计图中尽可能多并且正确地获取信息、利用数据进行分析、作出判断。 2. 选择合适的统计图。 扇形统计图的特点及作用。 扇形统计图是用整个圆的面积 表示总数 , 用圆内的扇形面积表 示各部分占总数的百分比。 扇形统计图 它可以清楚地表示出各部 分数量与总数之间的关系 。 扇形统计图 部分数量与部分数 量之间的关系 。 扇形统计图 三、知识点汇总 统计图 条形 折线 扇形 表示出各数量多少 表示出数量增减变化 表示出部分数量与总数的关系 根据数据的特点进行选择 选择合适的统计图 三、知识点汇总 1. 下面是我国 2006——2011 年年末电话用户数量的情况。 （教材 P102 第 6 题） 四、问题解决 （ 1 ） 2006 年末，移动电话用户比固定电话用户多百分之多少？ 2011 年呢？根据结果交流，和同学交流一下你的感想。 答： 2006 年末，移动电话用户比固定电话用户多 25.4% ； 2011 年末，移动电话用户比固定电话用户多 245.9% 。 我觉得移动电话将逐渐取代了固定电话。 46106 － 36779 ＝ 9327 （万户） 9327÷36779×100%≈25.4% 98625 － 28512 ＝ 70113 （万户） 70113÷28512×100%≈245.9% 四、问题解决 考点一：根据统计图解决问题 （ 2 ）请你完成下面的统计图。 四、问题解决 考点二：完成折线统计图 五、单元提升 李明每天的作息时间安排如下图。 答：李明每天花 1.92 小时做作业；花在上课的时间比做作业的时间更多 …… （ 1 ）李明每天花多少小时做作业？你还能得到哪些信息？ 做作业： 24×8% ＝ 1.92 （小时） （ 2 ）你认为李明的作息时间安排得合理吗？ （ 3 ）你的作息时间与李明的有什么不同？ 答：合理。 （教材 P100 第 1 题） 2. 空气的主要成分体积含量各占总体积百分比情况统计如下图。 （ 1 ）在 100L 空气中含有多少升氧气？ 答：在 100L 空气中含有 21 升氧气。 100×21% ＝ 21 （升） （ 2 ）估计一下，教室内大约有多少氧气？ 1% 一间普通教室一般长宽高分别为 8 米、 6 米 、 4 米。 空气： 8 ×6×4=192 （ m ） =192000 （ L ） 3 氧气： 192000 ×21%=40320 （升） 答：教室内大约有 40320 升氧气 . （教材 P101 第 3 题） 五、单元提升 3. 我国国土面积约 960 万平方千米，各种地形所占百分比如右图。 （ 1 ）请你计算各种地形的面积，填入下表。 （ 2 ）根据这些信息，你能提出什么数学问题？试着解答一下。 平原 12% 丘陵 10% 地 形 山地 高原 盆地 平原 丘陵 面积 / 万平方千米 316.8 249.6 182.4 115.2 96 （教材 P101 第 4 题） 五、单元提升 4. 下面是广东省 1990 年、 2000 年、 2010 年总常住人口和城镇常住人口变化的情况。 （教材 P101 第 5 题） 五、单元提升 （ 1 ）通过统计图中的数据，你能得到哪些有意义的信息？ 答：城镇常住人口占总常住人口比例逐年上升，说明农村往城市迁移人口逐渐增多。 四、问题解决 （ 2 ）你能根据图中的统计，完成下面的两个统计图吗？ 五、单元提升 六、拓展提升 1. 下表是我国土地利用类型的大致构成情况。 （ 1 ）耕地占可利用土地的百分之多少？ 1 － 21.6% ＝ 78.4% 13.5%÷78.4% ＝ 17.2% 答：耕地占可利用土地的 17.2% 。 （教材 P104 第 8 题） 六、拓展提升 1. 下表是我国土地利用类型的大致构成情况。 （ 2 ）请选用合适的统计图表示出上表中的相关信息。 可以选择扇形统计图。 （教材 P104 第 8 题） 七、拓展阅读 1. 收集数据，整理数据。 2. 计算各部分占总体的百分比。 3. 计算各个扇形的圆心角度数。 4. 写出统计图的标题，借助圆规和量角器完成扇形统计图 , 并在各扇形内注明 名称 和 百分比 。 完成教材整理与复习。 八、课后作业 数与形 8 人教版 · 六年级上册 第 1 课时 数与形 一、新课引入 1 ＋ 3 ＝ （ ） 4 1 ＋ 3 ＋ 5 ＝ （ ） 9 1 ＋ 3 ＋ 5 ＋ 7 ＝ （ ） 16 1 ＋ 3 ＋ 5 ＋ 7 ＋ 9 ＋ 11 ＋ 13 ＋ 15 ＋ 17 ＋ 19 ＝ （ ） 100 计算出结果。 二、例题讲解 观察一下，下面三幅图中分别有多少个小正方形？ 1+3= 1+3+5= 从左边图 1 到图 2 再到图 3 ，依次增加了多少个小正方形？如果用加法算式怎么表示？ 9 4 1 二、例题讲解 （ ） 1 1 ＝ 1 ＋ 3 ＝ 4 = （ ） 2 1 ＋ 3 ＋ 5 ＝ 9 = （ ） 2 2 3 观察一下，上面的图和下面的算式有什么关系？把算式补充完整。 我发现，算式左边的加数是大正方形右上角的小正方形和其他“ ” 形图形所包含的 小正方形个数之和正好是每行或每列小正方形个数的平方 。 2 1 ＋ 3 ＋ 5 ＋ 7 ＝（ ） 1 ＋ 3 ＋ 5 ＋ 7 ＋ 9 ＋ 11 ＋ 13 ＝（ ） 1. 你能利用规律直接写一写吗？ 4 7 2 2 如果遇到困难 , 可以画图来帮助。 如果遇到困难 , 可以画图来帮助。 2 2 二、例题讲解 1= 1 ＋ 3= 1 ＋ 3 ＋ 5 = 观察下面的算式有什么规律？ 从 1 开始 的 几个 连续奇数相加 , 和即是 几的平方 。 1+3+5+7 1 ＋ 3 ＋ 5 ＋ 7 ＋ 9 ＋ 11 ＋ 13 二、例题讲解 2. 利用规律填一填。 1 ＋ 3 ＋ 5 ＋ 7 ＋ 9 ＋ 11 ＋ 13 ＋ 15 ＋ 17 = （ ） 1+3+5+7+9+…+n =( ) n 个 二、例题讲解 计算 0 0 0 0 0 = 继续加下去，等号右边的分数越来越接近于 1 。 你能发现什么规律？ 二、例题讲解 =1 绿色圃中小学教育网 http://www.lspjy.com … 可以画个图来帮助思考。 计算 二、例题讲解 绿色圃中小学教育网 http://www.lspjy.com 绿色圃中小学教育网 http://www.lspjy.com 绿色圃中小学教育网 http://www.lspjy.com + + + + + =1 从图上可以看出，这些分数不断加下去，总和就是 1 。 有些问题通过画图，解决起来更直观。 计算 二、例题讲解 三、新知运用 1 ＋ 3 ＋ 5 ＋ 7 ＋ 5 ＋ 3 ＋ 1 ＝（ ） 1. 请根据例 1 的结论算一算。 ( 教材 P108 做一做第 1 题 ) 25 1 ＋ 3 ＋ 5 ＋ 7 ＋ 9 ＋ 11 ＋ 13 ＋ 11 ＋ 9 ＋ 7 ＋ 5 ＋ 3 ＋ 1 ＝（ ） 85 1 ＋ 3 ＋ 7 ＋9＋11＋13＝ （ ） 可以这么看： 44 2. 下面每个图中各有多少个红色小正方形和多少个蓝色小正方形？（ 教材 P108 做一做第 2 题 ） 照这样接着画下去，第 6 个图形有多少个红色小正方形和多少个蓝色小正方形？第 10 个图形呢？你能解释这其中的道理吗？ 第n个图形中就有 n个红色的小正方形 和 2n+6个蓝色小正方形。 三、新知运用 第6个图形中有 6个红色小正方形 和 2×6+6=18（个）蓝色小正方形； 第10个图形中有 10个红色小正方形 和 2×10+6=26（个）蓝色小正方形； 图形左右两边的蓝色正方体有 6 个，是不变的，图形上下的蓝色正方体个数是中间红色正方形的 2 倍。 四、课堂小结 回顾本节课，你学会了什么？ 从 1 开始 的 几个 连续奇数相加 , 和即是 几的平方 。 1+3+5+7+9+…+n =( ) n 个 五、课后作业 完成课本“练习二十二”第 109 页 第 1 题、 第 2 题。 数与形 8 人教版 · 六 年级上册 单元 整理与复习 一、学习目标 1．会用数形结合的方法解决一些数学问题。 2．在解决问题的过程中培养发现模式、应用模式的能力，提高推理能力。 3．在解决问题的过程中掌握和体会数形结合、极限等数学思想。 二、学习重难点 学习重点： 学习难点: 自主探索图形中隐藏着的数的规律，会利用图形来解决一些有关数的问题，并学会应用所发现的规律。 体会和掌握数形结合、归纳推理、极限等基本数学思想。 数形结合思想是学习数学的一种重要思想，运用数形结合的方法，探究数学规律，可以是数学问题解决起来更简单。 数 与 形 运用数形结合发现规律 极限思想 三、知识点汇总 四、问题解决 1. 下面每个图中最外圈有多少个小正方形？ 照这样画下去，第 4 个图形最外圈有（ ）个小正方形 。 40 3 － 1 ＝ 8 2 5 － 3 ＝ 16 2 2 7 － 5 ＝ 24 2 2 11 － 9 ＝ 40 2 2 照这样画下去，第 5 个图形最外圈有 （ ） 个小正方形 。 32 9 － 7 ＝ 32 2 2 （教材 P109 第 1 题） 考点一：运用数形结合发现规律 每个图中最外圈各有多少个小正方形？你能解释这其中的道理吗？ 16 8 24 32 40 8n 四、问题解决 1 3 6 10 15 21 照这样画下去，第10个图形下面的数字是多少？ 1. （教材 P109 第 2 题） 五、单元提升 1 2 3 4 5 6 7 8 9 10 1+2+3+4+5+6+7+8+9+10= (1+10) × 10 ÷ 2= 55 五、单元提升 1 3 6 10 15 21 由于数量为 1 、 3 、 6 、 10 、 15…… 相同 的小图形可以组成一个三角形，这些数也叫做“ 三角形数 ”。 五、单元提升 2. 下面每个三角形图各是由多少个小三角形组成的？如果小三角形的边长为 1 ，每个三角形图的周长分别是多少？每个三角形图包含小三角形的个数与这个三角形的周长之间有什么样的关系？ 三角形个数： 1 4 9 16 周 长： 3 6 9 12 小三角形的个数＝（周长 ÷3 ） ² 第 n 个图形 2 n 3n （教材 P110 第 3 题） 五、单元提升 3. 一条马路长 200 米 , 小亮和他的小狗分别以均匀的速度同时从马路的起点出发。当小亮走到这条马路一半的时候 , 小狗已到达马路的终点。然后小狗返回与小亮相向而行 , 遇到小亮以后再跑回终点，到达终点以后再与小亮相向而行 …… 直到小亮到达终点。小狗从出发开始，一共跑了多少米？ 小狗的速度等于小亮速度的 2 倍。 小狗的时间＝小亮走路的时间。 所以小狗跑的路程等于小亮走的路程的 2 倍。 答：小狗一共跑了 400 米。 200×2 ＝ 400 （米） 起点 终点 （教材 P110 第 4 题） 五、单元提升 4. 小兰和爸爸、妈妈一起步行到离家 800m 远的公园健身中心，用时 20 分钟。妈妈到了健身中心直接返回家里，还是用了 20 分钟。小兰和爸爸一起在健身中心锻炼了 10 分钟。然后，小兰跑步回到家中，用了 5 分钟，而爸爸是走回家中，用了 15 分钟。下面几个图哪个是描述妈妈离家时间和离家距离的关系？哪个是描述爸爸的？哪个是描述小兰的？ 小兰 妈妈 爸爸 （教材 P110 第 5 题） 五、单元提升 5. 小林、小强、小芳、小兵和小刚 5 人进行象棋比赛，每 2 人之间都要下一盘。小林已经下了 4 盘，小强下了 3 盘，小芳下了 2 盘，小兵下了 1 盘。请问：小刚一共下了几盘？分别和谁下的？ 用连线的方法试试。 （教材 P111 第 6 题） 五、单元提升 小林 小强 小芳 小兵 小刚 答：小刚一共下了 2 盘，分别和小林、小强下的。 5. 小林、小强、小芳、小兵和小刚 5 人进行象棋比赛，每 2 人之间都要下一盘。小林已经下了 4 盘，小强下了 3 盘，小芳下了 2 盘，小兵下了 1 盘。请问：小刚一共下了几盘？分别和谁下的？ 五、单元提升 6. 你能利用下面的图发现（ a+b ） 2 =a 2 +2ab+b 2 这一公式吗？利用你所学的面积计算的知识，探索一下。 分析解答： 大正方形面积（ a+b ） 2 。 a² ab ab b² 几个小图形面积和为 a 2 +ab+ab+b 2 =a 2 +2ab+b 2 。 因为，大正方形面积就等于几个小图形面积之和， 所以有（ a+b ） 2 =a 2 +2ab+b 2 。 （教材 P111 第 8 题） 五、单元提升 1. 我国宋代数学家杨辉在公元 1261 年撰写了 《 详解九章算法 》 ，他在这本著作中画了一个由数构成的三角形图，我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗？你能按照发现的规律把这个三角形表继续写下去吗？试试看。 1 6 15 20 15 6 1 六、拓展提升 三角形的两条斜边上都是数字 1 ，而其余的数都等于它肩上的两个数字相加 。 六、拓展提升 杨辉三角 《 详解九章算法 》 里记载过的表 杨辉 七、拓展阅读 　 我国北宋数学家贾宪（约公元 11 世纪）已经用过“杨辉三角”，这表明我国发现这个表不晚于 11 世纪。在欧洲，这个表被认为是法国数学家物理学家帕斯卡首先发现的 , 他们把这个表叫做帕斯卡三角。杨辉三角的发现要比欧洲早 500 年左右。 七、拓展阅读 完成教材整理与复习。 八、课后作业