- 2021-04-25 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学圆中分类讨论问题目归类举例三轮冲刺
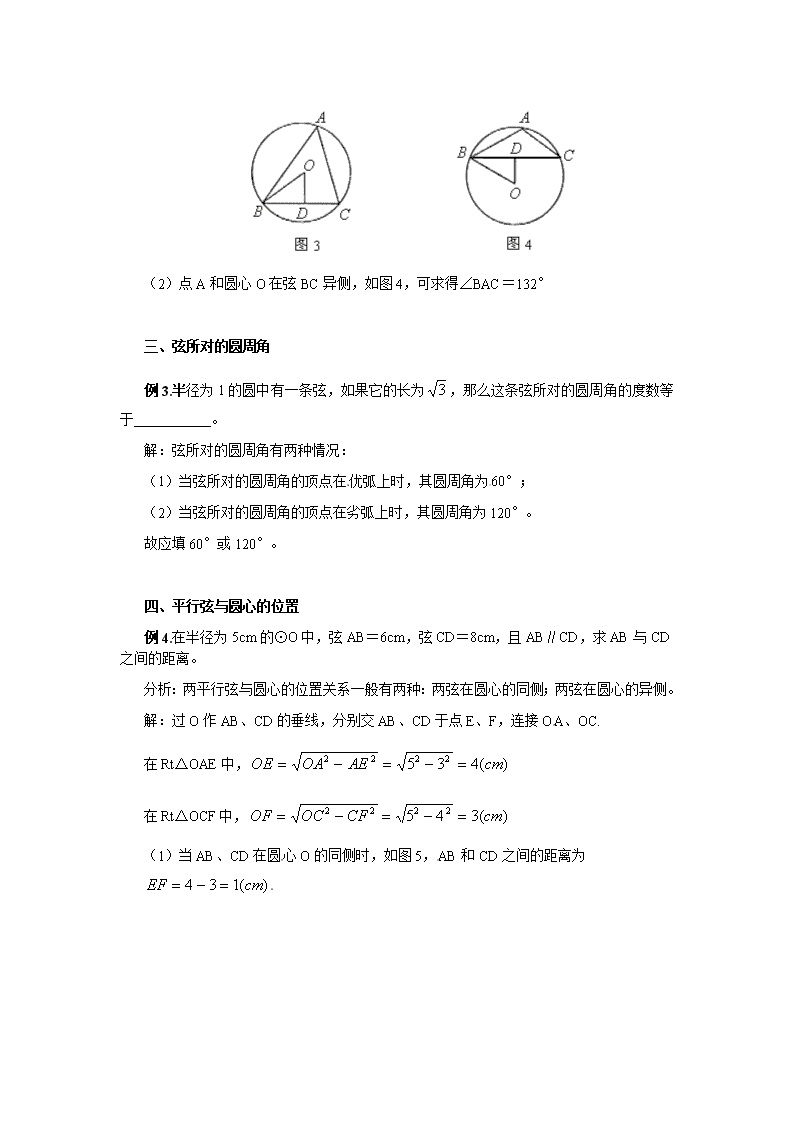
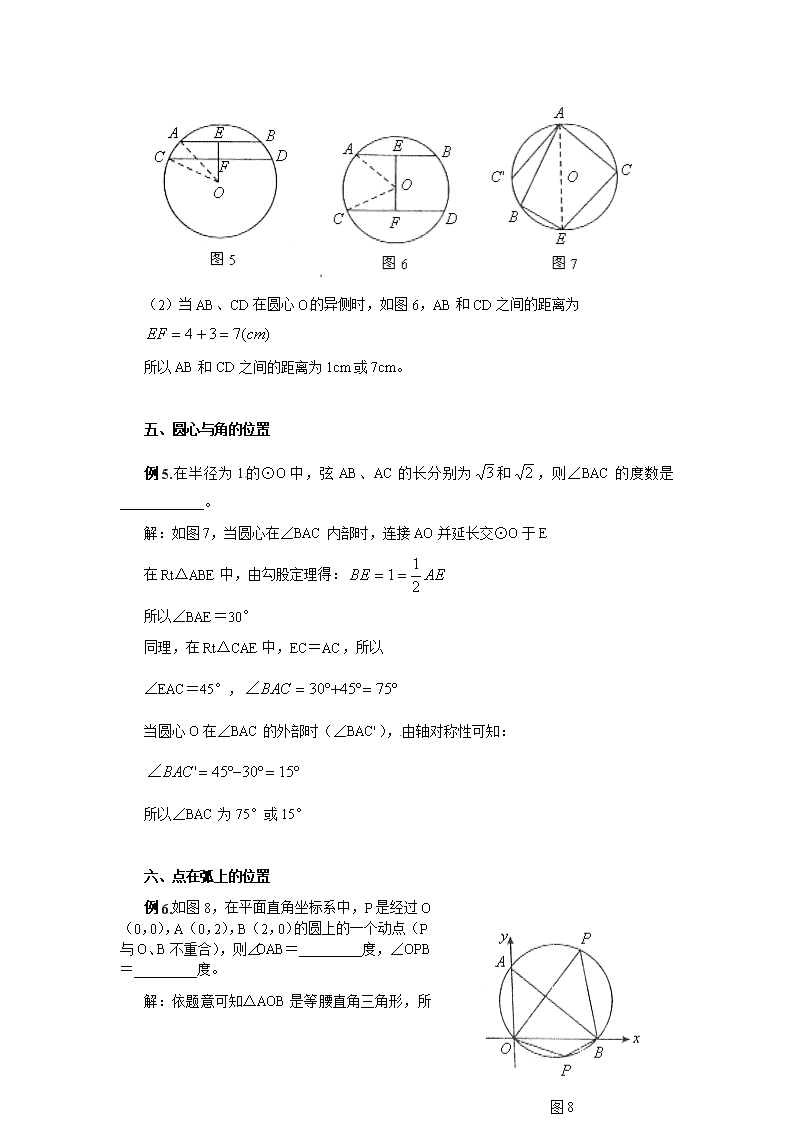
2013中考总结复习冲刺练:圆中分类讨论问题归类举例 圆既是轴对称图形,又是中心对称图形,还具有旋转不变性,圆的这些特性决定了关于圆的某些问题会有多解。解答这类问题时需要按照一定的标准,分成若干种情况,逐一加以讨论。这样可以避免漏解,培养同学们分析问题、解决问题的能力。本文就近年中考题举例说明如下。 一、点和圆的位置 凡涉及点与圆的位置关系问题,在没有指明其位置时,应考虑点在圆内、圆上、圆外三种可能情形。 例1.过不在⊙O上的一点A,作⊙O的割线,交⊙O于B、C,且AB·AC=64,OA=10,则⊙O的半径R为___________。 解:依题意,点A与⊙O的位置关系有两种: (1)点A在⊙O内,如图1,延长AO交⊙O于F,则 由相交弦定理得: 所以(负值已舍去) (2)点A在⊙O外,如图2, 此时 由割线定理得: 所以(负值已舍去) 故⊙O的半径R为或6。 二、点与弦的相对位置 例2.⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=48°,则∠BAC=_________。 解:(1)点A和圆心O在弦BC同侧,如图3,可求得∠BAC=∠BOD=48° (2)点A和圆心O在弦BC异侧,如图4,可求得∠BAC=132° 三、弦所对的圆周角 例3.半径为1的圆中有一条弦,如果它的长为,那么这条弦所对的圆周角的度数等于___________。 解:弦所对的圆周角有两种情况: (1)当弦所对的圆周角的顶点在优弧上时,其圆周角为60°; (2)当弦所对的圆周角的顶点在劣弧上时,其圆周角为120°。 故应填60°或120°。 四、平行弦与圆心的位置 例4.在半径为5cm的⊙O中,弦AB=6cm,弦CD=8cm,且AB∥CD,求AB与CD之间的距离。 分析:两平行弦与圆心的位置关系一般有两种:两弦在圆心的同侧;两弦在圆心的异侧。 解:过O作AB、CD的垂线,分别交AB、CD于点E、F,连接OA、OC. 在Rt△OAE中, 在Rt△OCF中, (1)当AB、CD在圆心O的同侧时,如图5,AB和CD之间的距离为 (2)当AB、CD在圆心O的异侧时,如图6,AB和CD之间的距离为 所以AB和CD之间的距离为1cm或7cm。 五、圆心与角的位置 例5.在半径为1的⊙O中,弦AB、AC的长分别为和,则∠BAC的度数是____________。 解:如图7,当圆心在∠BAC内部时,连接AO并延长交⊙O于E 在Rt△ABE中,由勾股定理得: 所以∠BAE=30° 同理,在Rt△CAE中,EC=AC,所以 ∠EAC=45°, 当圆心O在∠BAC的外部时(∠BAC'),由轴对称性可知: 所以∠BAC为75°或15° 六、点在弧上的位置 例6.如图8,在平面直角坐标系中,P是经过O(0,0),A(0,2),B(2,0)的圆上的一个动点(P与O、B不重合),则∠OAB=_________度,∠OPB=_________度。 图8 解:依题意可知△AOB 是等腰直角三角形,所以∠OAB=45° 当动点P在上时,∠OPB=∠OAB=45° 当动点P在上时,∠OPB=180°-45°=135° 故∠OPB为45°或135°。 七、相交两圆的圆心与公共弦的位置 例7.已知半径为4和的两圆相交,公共弦长为4,则两圆的圆心距为_________。 分析:相交两圆圆心的位置有在公共弦的同侧和异侧两种情况。 解:如图9、图10, 在中, 在中, (1)当圆心在公共弦AB的同侧时,如图9 (2)当圆心在公共弦AB的异侧时,如图10 八、直线与圆的位置 例8.两圆的半径分别为4和2 ,如果它们的两条公切线互相垂直,求两圆的圆心距。 分析:两圆的公切线有内公切线和外公切线两种,公切线互相垂直,有三种情况。 解:(1)当内公切线与外公切线垂直时,如图11,AB切⊙于A,切⊙于B,EF切⊙于E,切⊙于F,AB⊥EF于D。 由切线定理,得: 所以 故有 (2)当内公切线垂直时,如图12,作,交点为E,则 (3)当外公切线垂直时,如图13,作于G,则 .查看更多