中考数学压轴题专项训练题附答案

中考数学压轴题专项训练题附答案

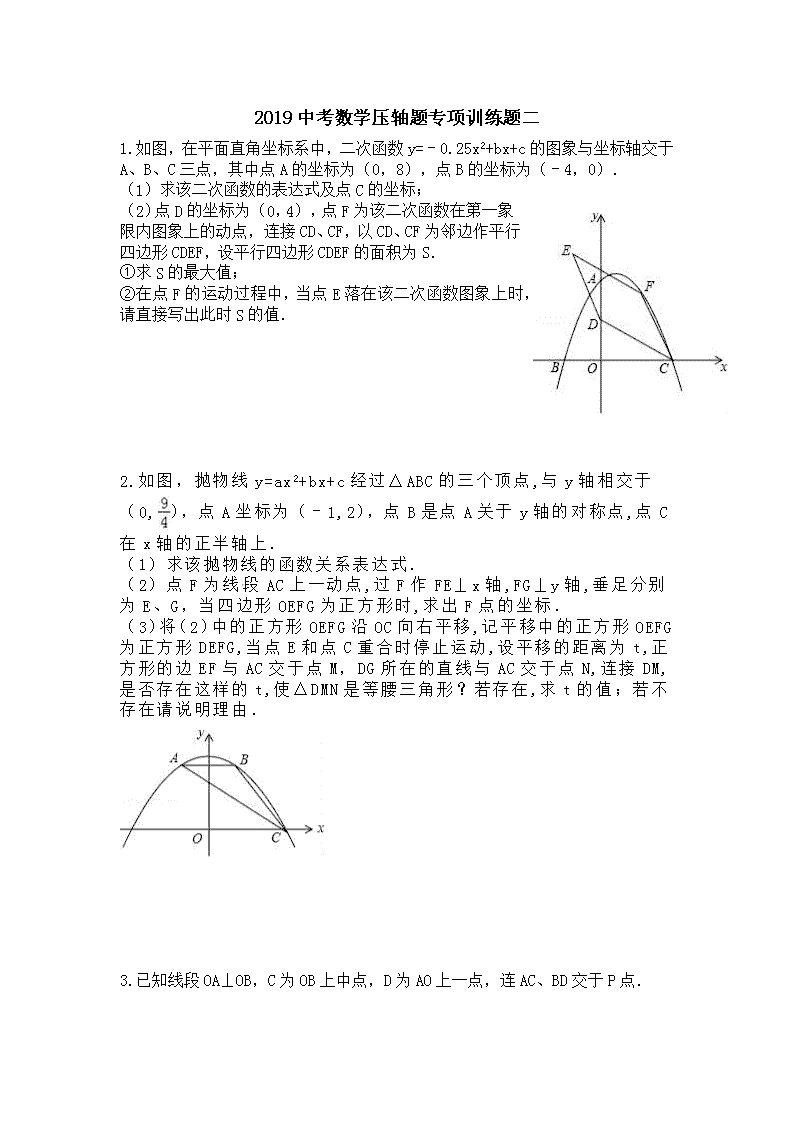
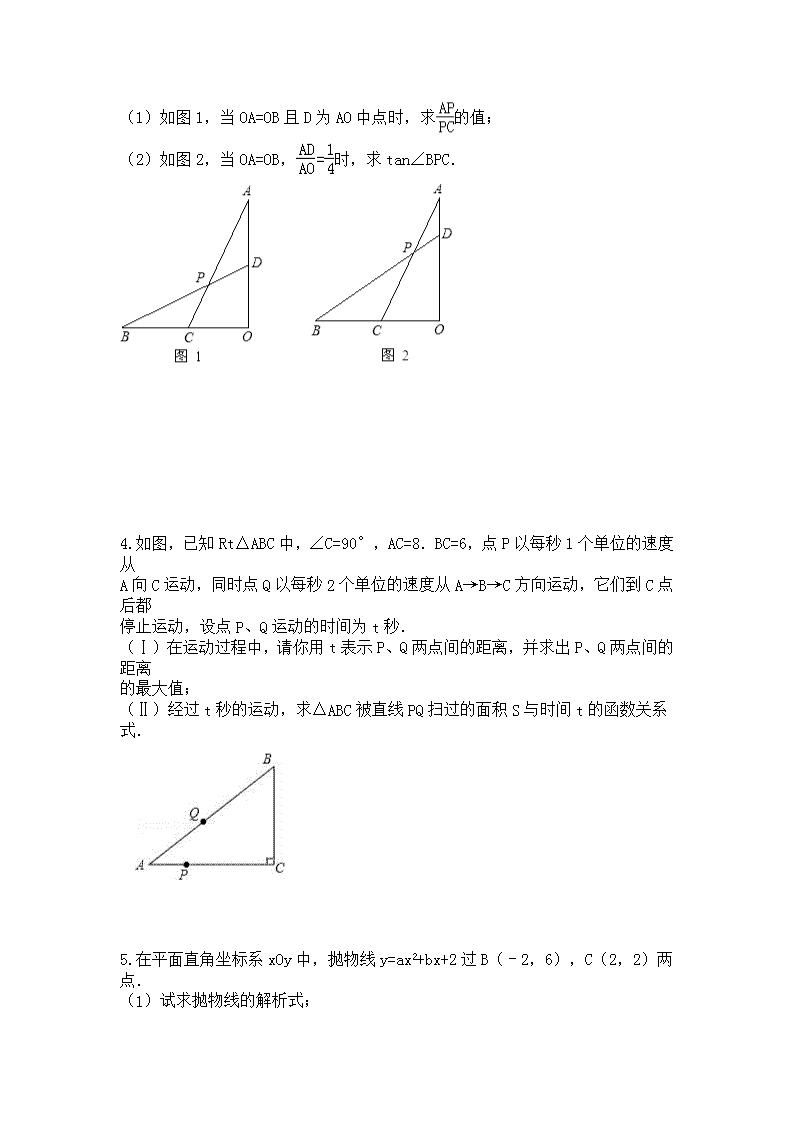
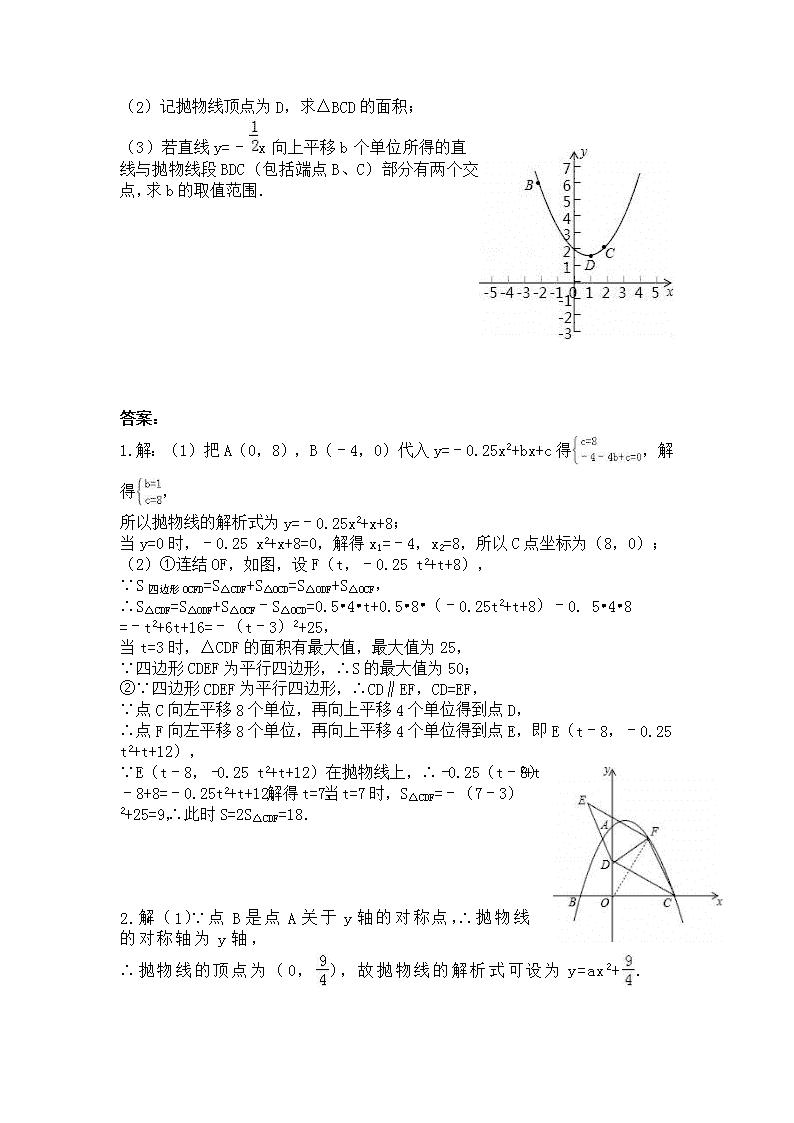
‎2019中考数学压轴题专项训练题二 如图，在平面直角坐标系中，二次函数y=﹣0.25x2+bx+c的图象与坐标轴交于A、B、C三点，其中点A的坐标为（0，8），点B的坐标为（﹣4，0）．‎ ‎（1）求该二次函数的表达式及点C的坐标；‎ ‎（2）点D的坐标为（0，4），点F为该二次函数在第一象限内图象上的动点，连接CD、CF，以CD、CF为邻边作平行四边形CDEF，设平行四边形CDEF的面积为S．‎ ‎①求S的最大值； ‎ ‎②在点F的运动过程中，当点E落在该二次函数图象上时，请直接写出此时S的值．‎ 如图，抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于（0,），点A坐标为（﹣1,2），点B是点A关于y轴的对称点,点C在x轴的正半轴上．‎ ‎（1）求该抛物线的函数关系表达式．‎ ‎（2）点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G，当四边形OEFG为正方形时,求出F点的坐标．‎ ‎（3）将（2）中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M，DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形？若存在,求t的值；若不存在请说明理由．‎ 已知线段OA⊥OB，C为OB上中点，D为AO上一点，连AC、BD交于P点．‎ ‎（1）如图1，当OA=OB且D为AO中点时，求的值；‎ ‎（2）如图2，当OA=OB，时，求tan∠BPC．‎ ‎ ‎ 如图，已知Rt△ABC中，∠C=90°，AC=8．BC=6，点P以每秒1个单位的速度从 A向C运动，同时点Q以每秒2个单位的速度从A→B→C方向运动，它们到C点后都 停止运动，设点P、Q运动的时间为t秒．‎ ‎（Ⅰ）在运动过程中，请你用t表示P、Q两点间的距离，并求出P、Q两点间的距离 的最大值；‎ ‎（Ⅱ）经过t秒的运动，求△ABC被直线PQ扫过的面积S与时间t的函数关系式．‎ ‎ ‎ 在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．‎ ‎（1）试求抛物线的解析式；‎ ‎（2）记抛物线顶点为D，求△BCD的面积；‎ ‎（3）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围． ‎ 答案：‎ ‎1.解：（1）把A（0，8），B（﹣4，0）代入y=﹣0.25x2+bx+c得，解得，‎ 所以抛物线的解析式为y=﹣0.25x2+x+8；‎ 当y=0时，﹣0.25 x2+x+8=0，解得x1=﹣4，x2=8，所以C点坐标为（8，0）；‎ ‎（2）①连结OF，如图，设F（t，﹣0.25 t2+t+8），‎ ‎∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF，‎ ‎∴S△CDF=S△ODF+S△OCF﹣S△OCD=0.5•4•t+0.5•8•（﹣0.25t2+t+8）﹣0. 5•4•8‎ ‎=﹣t2+6t+16=﹣（t﹣3）2+25，‎ 当t=3时，△CDF的面积有最大值，最大值为25，‎ ‎∵四边形CDEF为平行四边形，∴S的最大值为50；‎ ‎②∵四边形CDEF为平行四边形，∴CD∥EF，CD=EF，‎ ‎∵点C向左平移8个单位，再向上平移4个单位得到点D，‎ ‎∴点F向左平移8个单位，再向上平移4个单位得到点E，即E（t﹣8，﹣0.25 t2+t+12），‎ ‎∵E（t﹣8，﹣0.25 t2+t+12）在抛物线上，∴﹣0.25（t﹣8）2+t﹣8+8=﹣0.25t2+t+12，解得t=7，当t=7时，S△CDF=﹣（7﹣3）2+25=9，∴此时S=2S△CDF=18．‎ ‎2.解：（1）∵点B是点A关于y轴的对称点，∴抛物线的对称轴为y轴，‎ ‎∴抛物线的顶点为（0，），故抛物线的解析式可设为y=ax2+．‎ ‎∵A（﹣1，2）在抛物线y=ax2+上，∴a+=2，解得a=﹣，‎ ‎∴抛物线的函数关系表达式为y=﹣x2+；‎ ‎（2）①当点F在第一象限时，如图1，令y=0得，﹣x2+=0，‎ 解得：x1=3，x2=﹣3，∴点C的坐标为（3，0）．‎ 设直线AC的解析式为y=mx+n，则有，解得，‎ ‎∴直线AC的解析式为y=﹣x+．‎ 设正方形OEFG的边长为p，则F（p，p）．‎ ‎∵点F（p，p）在直线y=﹣x+上，∴﹣p+=p，解得p=1，‎ ‎∴点F的坐标为（1，1）．‎ ‎②当点F在第二象限时，‎ 同理可得：点F的坐标为（﹣3，3），此时点F不在线段AC上，故舍去．‎ 综上所述：点F的坐标为（1，1）；‎ ‎（3）过点M作MH⊥DN于H，如图2，则OD=t，OE=t+1．‎ ‎∵点E和点C重合时停止运动，∴0≤t≤2．‎ 当x=t时，y=﹣t+，则N（t，﹣t+），DN=﹣t+．‎ 当x=t+1时，y=﹣（t+1）+=﹣t+1，则M（t+1，﹣t+1），ME=﹣t+1．‎ 在Rt△DEM中，DM2=12+（﹣t+1）2=t2﹣t+2．‎ 在Rt△NHM中，MH=1，NH=（﹣t+）﹣（﹣t+1）=，∴MN2=12+（）2=．‎ ‎①当DN=DM时，（﹣t+）2=t2﹣t+2，解得t=；‎ ‎②当ND=NM时，﹣t+==，解得t=3﹣；‎ ‎③当MN=MD时，=t2﹣t+2，解得t1=1，t2=3．‎ ‎∵0≤t≤2，∴t=1．‎ 综上所述：当△DMN是等腰三角形时，t的值为，3﹣或1．‎ ‎3.解：（1）过D作DE∥CO交AC于E，‎ ‎∵D为OA中点，∴AE=CE=，，‎ ‎∵点C为OB中点，∴BC=CO，，‎ ‎∴，∴PC==，∴=2；‎ ‎（2）过点D作DE∥BO交AC于E，‎ ‎∵，∴==，∵点C为OB中点，∴，‎ ‎∴，∴PC==，‎ 过D作DF⊥AC，垂足为F，设AD=a，则AO=4a，‎ ‎∵OA=OB，点C为OB中点，∴CO=2a，‎ 在Rt△ACO中，AC===2 a，‎ 又∵Rt△ADF∽Rt△ACO，∴，∴AF=，DF=，‎ PF=AC﹣AF﹣PC=2 a﹣﹣=，tan∠BPC=tan∠FPD==．‎ ‎ ‎ ‎4.解：（Ⅰ）分两种情况考虑：‎ 当Q在AB边上时，过Q作QE⊥AC，交AC于点E，连接PQ，如图1所示：‎ ‎ ‎ ‎∵∠C=90°，∴QE∥BC，∴△ABC∽△AQE，∴==，‎ 在Rt△ABC中，AC=8，BC=6，根据勾股定理得：AB=10，‎ ‎∵AQ=2t，AP=t，∴==，整理得：PE=t，QE=t，‎ 根据勾股定理得：PQ2=QE2+PE2，整理得：PQ=t；‎ 当Q在BC边上时，连接PQ，如图2所示：‎ ‎ ‎ 由AB+BQ=2t，AB=10，得到BQ=2t﹣10，CQ=BC﹣BQ=6﹣（2t﹣10）=16﹣2t，‎ 由AP=t，AC=8，得到PC=8﹣t，‎ 根据勾股定理得：PQ==，‎ 当Q与B重合时，PQ的值最大，则当t=5时，PQ最大值为3；‎ ‎（Ⅱ）分两种情况考虑：‎ 当Q在AB边上时，如图1，△ABC被直线PQ扫过的面积为S△AQP=‎ 此时S=AP•QE=t•t=t2（0＜t≤5）；‎ 当Q在BC边上时，△ABC被直线PQ扫过的面积为S四边形ABQP，‎ 此时S=S△ABC﹣S△PQC=×8×6﹣（8﹣t）（16﹣2t）=﹣t2+16t﹣40（5＜t≤8）．‎ 综上，经过t秒的运动，△ABC被直线PQ扫过的面积S与时间t的函数关系式为 ‎5.解：（1）由题意解得，∴抛物线解析式为y=x2﹣x+2．‎ ‎（2）∵y=x2﹣x+2=（x﹣1）2+．∴顶点坐标（1，），‎ ‎∵直线BC为y=﹣x+4，∴对称轴与BC的交点H（1，3），‎ ‎∴S△BDC=S△BDH+S△DHC=•3+•1=3．‎ ‎（3）由消去y得到x2﹣x+4﹣2b=0，‎ 当△=0时，直线与抛物线相切，1﹣4（4﹣2b）=0，∴b=，‎ 当直线y=﹣x+b经过点C时，b=3，当直线y=﹣x+b经过点B时，b=5，‎ ‎∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，‎ ‎∴＜b≤3．‎