初中数学中考总复习课件PPT：第26课时 与圆有关的计算

初中数学中考总复习课件PPT：第26课时 与圆有关的计算

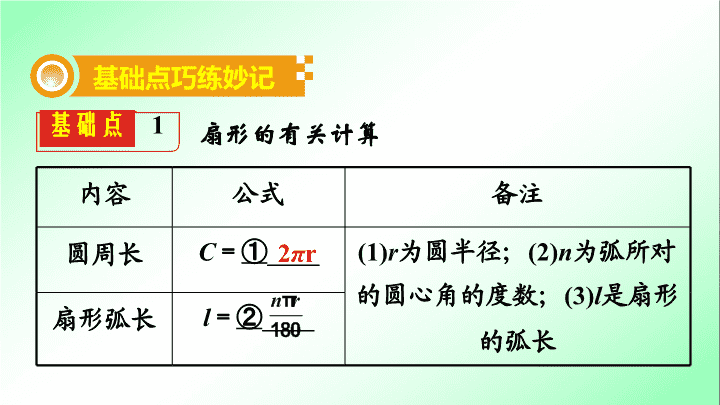
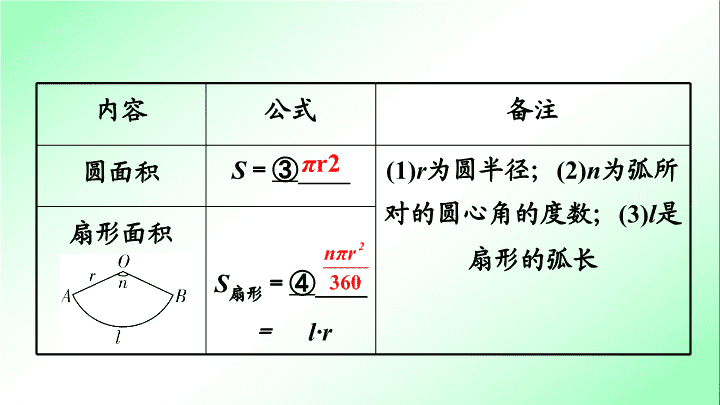
第一部分 夯实基础　提分多 第 六 单元 圆 第 2 6 课时 与圆有关的计算 基础点 1 扇形的有关计算 基础点巧练妙记 内容 公式 备注 圆周长 C ＝ ① ____ (1) r 为圆半径； (2) n 为弧所对的圆心角的度数； (3) l 是扇形的弧长 扇形弧长 l ＝ ② ____ 2 π r 内容 公式 备注 圆面积 S ＝ ③ ____ (1) r 为圆半径； (2) n 为弧所对的圆心角的度数； (3) l 是扇形的弧长 扇形面积 S 扇形 ＝ ④ ____ ＝ l·r π r2 1 ．已知一个扇形的弧长为 5π cm ，圆心角是 150° ，则它的半径长为 ( 　　 ) A ． 6 cm 　　 B ． 5 cm 　　 C ． 4 cm 　　 D ． 3 cm 2 ．如图， PA 、 PB 是⊙ O 的切线，切点分别为 A 、 B . 若 OA ＝ 2 ，∠ P ＝ 60° ，则 的长为 ( 　　 ) A. π 　　　 B. π C. π 　　　 D. π 练 提 分 必 A C 基础点 2 圆锥的有关计算 圆锥 S 底面圆＝ π r 2 C 底面圆＝ 2π r r 为底面圆半径 (1) 圆锥的侧面展开图是 ⑤ ______ ； (2) 圆锥底面圆的周长等于其侧面展开图 ( 扇形 ) 的 ⑥ ________ ； (3) 圆锥的母线长等于其侧面展开 扇形 弧长 圆锥 S 底面圆 ＝ π r 2 C 底面圆 ＝ 2π r r 为底面圆半径 图 ( 扇形 ) 的 ⑦ ______ ； (4) 底面周长： C ＝ ＝ 2π r ； (5) 圆锥的轴截面是等腰三角形，圆锥的母线长 l 、底面圆半径 r 和圆锥的高 h ，这三个量之间的数量关系为 ＋ ＝ 半径 基础点 3 正多边形与圆 设正 n 边形的边长为 a ，则边心距 r ＝ ；正 n 边形的周长 L ＝ na ；正 n 边形的面积 S ＝ Lr ＝ nar ；中心角 θ ＝ . 基础点 4 阴影部分面积的有关计算 求与圆有关的不规则图形的面积时，最基本的思想就是转化思想，即把所求的不规则图形的面积转化为规则图形的面积．常用的方法有： 方法 示意图 (1) 直接用公式求解； 方法 示意图 (2) 将所求面积分割后 ， 利用规则图形的面积相加减求解； (3) 将阴影中某些图形等积变形后移位 ， 重组成规则图形求解； 方法 示意图 (4) 将所求面积分割后，利用旋转将部分阴影图形移位后，重组成规则图形求解； (5) 将阴影图形看成是一些基本图形覆盖而成的重叠部分，用整体和差法求解． S 阴影 ＝ AB 2 － AB 2 ＝ ( － 1) AB 2 练习 1 　 (2017 临沂 ) 如图， AB 是⊙ O 的直径， BT 是⊙ O 的切线，若∠ ATB ＝ 45 ° ， AB ＝ 2 ，则阴影部分的面积是 ( 　　 ) A ． 2 B. - π C ． 1 D. + π 类型 阴影部分面积的计算 重难点精讲优练 C 【解析】 设 AT 与⊙ O 交于点 C ，由 AB 是⊙ O 的直径可得∠ ACB ＝90°，又∵∠ ATB ＝45°，∴ AC ＝ BC ＝ CT ，∴ S 阴影＝ S △ BCT ，再由 AB ＝2可得 AT ＝ ，∴ CT ＝ BC ＝ ，则 S 阴影＝ S △ BCT ＝ CT • BC ＝ × × ＝1. 练习 2 　如图， AB 是 ⊙ O 的直径，点 E 为 BC 的中点， AB ＝ 4 ， ∠ BED ＝ 120° ，则图中阴影部分的面积之和为 ( 　　 ) A. B. 2 C. D. 1 练习 2 题图 A 【解析】 如解图，连接 AE ， OD ， OE ，∵ AB 是⊙ O 的直径，∴∠ AEB ＝ 90° ，又∵∠ BED ＝ 120° ，∴∠ AED ＝ 30° ，∴∠ AOD ＝ 2∠ AED ＝ 60° ，∵ OA ＝ OD ，∴△ AOD 是等边三角形，∴∠ OAD ＝ 60°.∵ 点 E 为 BC 的中点，∠ AEB ＝ 90° ，∴ AB ＝ AC ， ∴△ ABC 是等边三角形，边长是 4 ，△ EDC 是等边三角形，边长是 2 ，∴∠ BOE ＝∠ EOD ＝ 60° ，∴ BE 和弦 BE 围成的部分的面积＝ DE 和弦 DE 围成的部分的面积， ∴ S 阴影 ＝ S △ EDC ＝ EC · CD ·sin60° ＝ ×2×2× ＝ . 练习 3 　如图， AB 是圆 O 的直径，弦 CD ⊥ AB ，∠ CDB ＝ 30 ° ， CD ＝ 2 ，则阴影部分的面积为 ( 　　 ) A. 4π B. 2π C. π D. 练习 3 题图 D