中考总复习相似三角形导学案

中考总复习相似三角形导学案

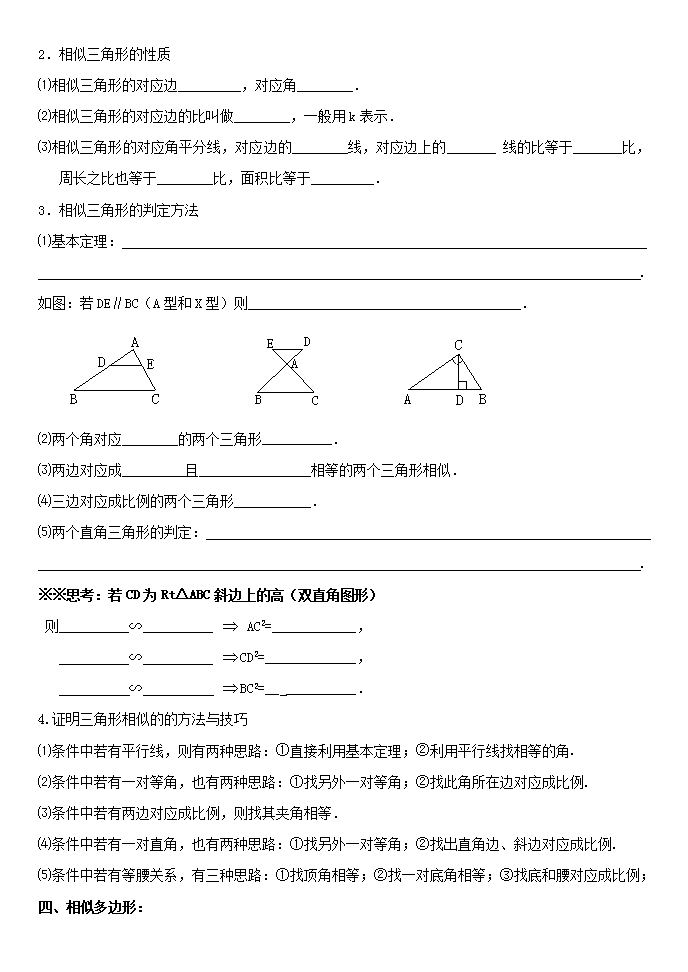
相似三角形 基础知识点 考点 课 标 要 求 知识与技能目标 了解 理解 掌握 灵活应用 图形的相似 比例的基本性质、线段的比、成比例线段 ‎∨‎ 认识图形的相似、探索相似图形的性质 ‎∨‎ 相似多边形的对应角相等，对应边成比例，面积的比等于对应边比的平方 ‎∨‎ 两个三角形相似的概念，图形的位似 ‎∨‎ 探索两个三角形相似的条件 ‎∨‎ 利用位似将一个图形放大或缩小 ‎∨‎ 一、比例的基本性质：‎ ‎1.若，那么，即：比例的内向之积等于外向之积；‎ 反之也成立：即若，那么；‎ ‎ 思考：由还可以推出那么些比例等式呢？‎ ‎2．合比性质：若，那么 ‎3．等比性质：若，则.‎ 例题：若满足，则 .(利用等比性质求)‎ 二、线段的比、成比例线段、黄金分割 ‎1.线段的比： ；‎ 这里应该注意的问题是：⑴ ；‎ ⑵ .‎ ‎2.比例线段： .‎ ‎3.黄金分割： ‎ ‎ .‎ 三、相似三角形：‎ ‎1．概念：三边对应成_________，三个角对应________的两个三角形叫做相似三角形．‎ ‎2．相似三角形的性质 ‎⑴相似三角形的对应边_________，对应角________．‎ ‎⑵相似三角形的对应边的比叫做________，一般用k表示．‎ ‎⑶相似三角形的对应角平分线，对应边的________线，对应边上的_______线的比等于_______比，周长之比也等于________比，面积比等于_________．‎ ‎3．相似三角形的判定方法 ‎⑴基本定理： ‎ ‎ .‎ 如图：若DE∥BC（A型和X型）则_______________________________________．‎ ‎ ‎ ‎⑵两个角对应 的两个三角形__________．‎ ‎⑶两边对应成_________且 相等的两个三角形相似．‎ ‎⑷三边对应成比例的两个三角形___________．‎ ‎⑸两个直角三角形的判定： ‎ ‎ .‎ ‎※※思考：若CD为Rt△ABC斜边上的高（双直角图形）‎ ‎ 则 ∽ AC2=____________，‎ ‎ ∽ CD2=_____________，‎ ‎ ∽ BC2=__ __________．‎ ‎4.证明三角形相似的的方法与技巧 ‎⑴条件中若有平行线，则有两种思路：①直接利用基本定理；②利用平行线找相等的角.‎ ‎⑵条件中若有一对等角，也有两种思路：①找另外一对等角；②找此角所在边对应成比例.‎ ‎⑶条件中若有两边对应成比例，则找其夹角相等．‎ ⑷条件中若有一对直角，也有两种思路：①找另外一对等角；②找出直角边、斜边对应成比例.‎ ⑸条件中若有等腰关系，有三种思路：①找顶角相等；②找一对底角相等；③找底和腰对应成比例；‎ 四、相似多边形：‎ ‎1.定义： ‎ ‎ .‎ ‎2.相似多边形的性质：‎ ⑴ ；‎ ⑵ .‎ 五、位似图形：‎ ‎1.定义： ‎ ‎ .‎ ‎2.位似图形的性质：‎ ⑴ ；‎ ⑵ .‎ ‎3.位似图形的作用： .‎ 解题指导 ‎【例1】已知，【 】‎ A. B. C. D. ‎ 及时练习： ‎ ‎1.如图，乐器上的一根弦cm，两个端点、固定在乐器板面上，支撑点是靠近点 黄金分割点，支撑点是靠近点的黄金分割点，则　　　　　cm，　　　　　cm．‎ Ａ D C B ‎2. （2000•山西）请阅读下面材料，并回答所提出的问题． 三角形内角平分线性质定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例． 已知：如图，△ABC中，AD是角平分线． 求证： ‎ ‎ 分析：要证 ，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似．‎ ‎ 现在B、D、C在一直线上，△ABD与△ADC不相似，需要考虑用别的方法换比．在比例式 ‎ ‎ 中，AC恰是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD，交BA的延长线于E，从而得 ‎ 到BD、DC、AB的第四比例项AE，这样，证明 ,就可以转化成证AE=AC． 证明：过C作CE∥DA，交BA的延长线于E． CE∥DA⇒ （1）上述证明过程中，用到了哪些定理？（写对两个定理即可）‎ ‎ （2）在上述分析、证明过程中，主要用到了下列三种数学思想的哪一种？‎ ‎ 选出一个填在后面的括号内． [ ] ①数形结合思想； ②转化思想； ③分类讨论思想．‎ ‎（3）用三角形内角平分线性质定理解答问题： 已知：如图，△ABC中，AD是角平分线，AB=5cm，AC=4cm，BC=7cm．求BD的长．‎ ‎ ‎ ‎【例2】下列四个三角形中，与左图中的三角形相似的是 【 】‎ ‎ A．‎ B．‎ C．‎ D．‎ ‎ ‎【例3】（2010•衡阳）如图6，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延 ‎ 长线于点F，BG⊥AE，垂足为G，BG=，则ΔCEF的周长为 【 】‎ ‎ A.8 B.9.5 C.10 D.11.5‎ ‎ ‎ ‎ 例题4‎ ‎【例4】如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，‎ 则△DEF的面积与△ABC的面积之比等于 1：3．‎ ‎【例5】花丛中有一路灯杆AB.在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH＝5米.如果小明的身高为1.7米，求路灯杆AB的高(精确到0.1米)． ‎ ‎ ‎【例6】如图，等腰梯形ABCD中，AD∥BC，AD=3，BC=7，∠B=60°，P为下底BC上一点（不与B、C 重合），过P点作PE交DC于E，使得∠APE=∠B． （1）求等腰梯形的腰长； （2）证明：△ABP∽△PCE； （3）在底边BC上是否存在一点P，使得DE：EC=5：3？如果存在，求出BP的长；如果不存在，请说 明理由．‎ ‎【例7】如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面 A B C D 例题7‎ 积比是 （ ）‎ A.3：4 B.5：8 C.9：16 D.1：2‎ 例题8‎ ‎【例8】如图，与是位似图形，‎ 且位似比是，若AB=2cm，则 cm，‎ 并在图中画出位似中心O．‎ ‎【例9】如图(十四)，不等长的两对角线AC、BD相交于O点，‎ ‎ 且将四边形ABCD分成甲、乙、丙、丁四个三角形。‎ ‎ 若OA：OC =OB：OD =1：2，则此四个三角形的关系，‎ 甲 O C D B A 乙 丙 丁 ‎ 下列叙述何者正确？ 【 】‎ ‎ (A) 甲丙相似，乙丁相似 ‎ ‎(B) 甲丙相似，乙丁不相似 ‎ (C) 甲丙不相似，乙丁相似 ‎ ‎(D) 甲丙不相似，乙丁不相似。‎ ‎【例10】如图，在梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE交AC于F，BE的延长线交CD的延长线于G． （1）求证： ； （2）若GE=2，BF=3，求线段EF的长．‎ ‎【例10】如图，在平面直角坐标系中，直线交轴于点，交轴于点，抛物线的图象过点，并与直线相交于、两点.‎ ‎ 求抛物线的解析式（关系式）；‎ ‎ 过点作交轴于点，求点的坐标；‎ ‎ 除点外，在坐标轴上是否存在点，使得是直角三角形？若存在，请求出点的坐标，若不存在，请说明理由.‎