- 2021-04-23 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小升初数学模拟试卷(25)
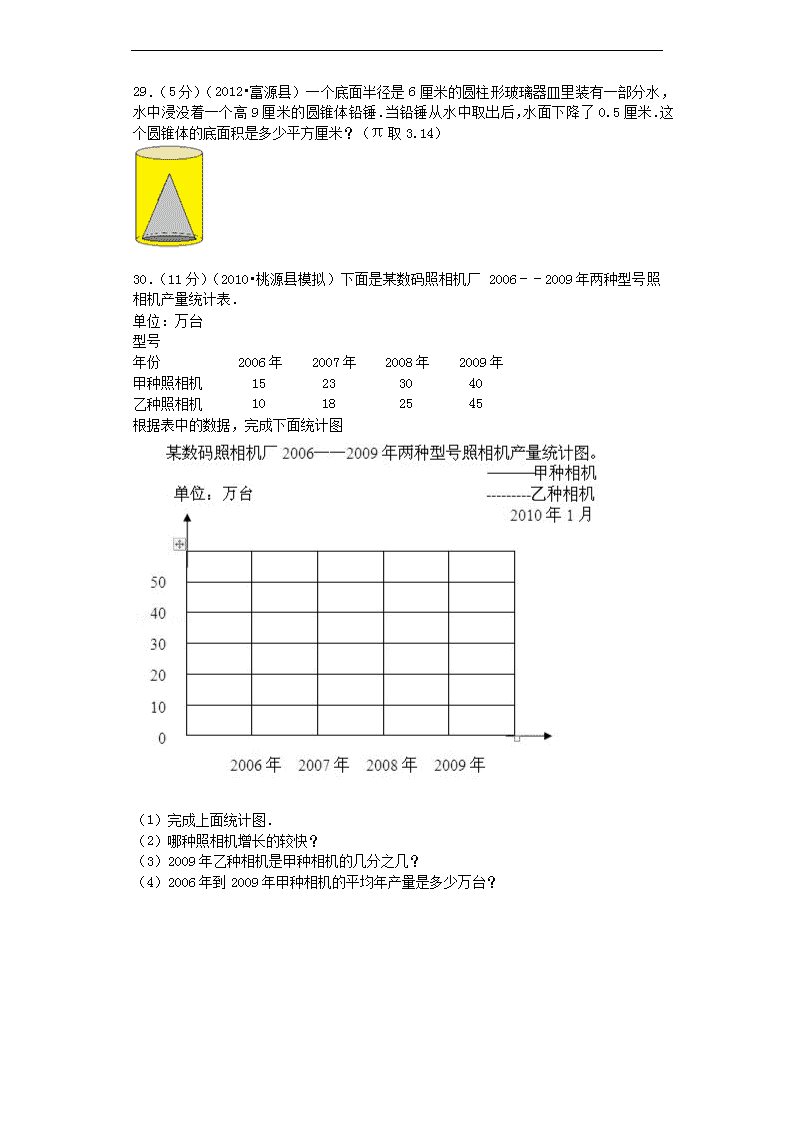
人教新课标小升初数学模拟试卷(25) 1.(2分)一个九位数,最高位是最小的奇数,千万位是最大的一位数,万位最小的质数,百位数最小的合数,其余各位都是零,这个数是 ,省略亿后面的尾数约是 . 2.(2分)(2014•孝感模拟)n=,m和 n成 比例;若a×3=b×5,a:b= . 3.(1分)(2013•东城区模拟)某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层要48秒,那么以同样的速度往上走到七层,还需要 秒才能到达. 4.(4分)(2012•广元模拟)3÷ = ÷24==75%= 折. 5.(3分)(2012•富源县)如图中圆柱的底面半径是 ,把这个圆柱的侧面展开可以得到一个长方形,这个长方形的面积是 ,这个圆柱体的体积是 .(圆周率为π) 6.(1分)(2012•富源县)1千克盐水含盐50克,盐是盐水的 %. 7.(1分)(2012•富源县)一所学校男学生与女学生的比是4:5,女学生比男学生人数多 %. 8.(1分)(2012•富源县)一座城市地图中两地图上距离为10cm,表示实际距离30km,该幅地图的比例尺是 . 9.(1分)(2012•富源县)自然数(0除外)不是质数,就是合数. .(判断对错) 10.(1分)(2012•富源县)小于五分之四而大于五份之二的分数只有五份之三. .(判断对错) 11.(1分)(2012•富源县)一个圆柱与一个圆锥等底等高,他们的体积和是36立方米,那么圆锥的体积是9立方米. .(判断对错) 12.(1分)(2014•广州)生产的90个零件中,有10个是废品,合格率是90%. (判断对错). 13.(1分)(2012•富源县)“一只青蛙四条腿,两只眼睛,一张嘴;两只青蛙八条腿,四只眼睛,两张嘴,三只青蛙…那么青蛙的只数与腿的条数成正比例关系” .(判断对错) 14.(1分)(2012•平坝县)2008年的1月份、2月份、3月份一共有( )天. A.89 B.90 C.91 D.92 15.(1分)(2012•富源县)把一个平行四边形任意分割成两个梯形,这两个梯形中( ) 总是相等. A.高 B.上下两底的和 C.周长 D.面积 16.(1分)(2012•富源县)一个长方形长5厘米,宽3厘米,表示( )几分之几. A.长比宽多 B.长比宽少 C.宽比长少 D.宽比长多 17.(1分)(2012•平坝县)一个分数的分子缩小3倍,分母扩大3倍,分数值就缩小( )倍. A.3 B.6 C.9 D.不变 18.(1分)(2014•博野县模拟)下列x和y成反比例关系的是( ) A.y=3+x B.x+y= C.x=y D.y= 19.(12分)直接写出得数. 26×50= 25×0.2= 10﹣0.86= 24×= ÷3= 125%×8= 4.8÷0.8= 8÷= 12×(+)= 1﹣1÷9= ×0= 2.5×3.5×0.4= 20.(6分) 脱式计算. 25×+2.5% 9.6﹣11÷7+×4 12×[(﹣)×3] 21.(6分)(2012•晋城)解比例和方程. (1)5.4+2x=8.6 (2)2.5:5=x:8 (3)0.2=1﹣. 22.(6分)(2012•富源县)列式计算. (1)180比一个数的50%多10,这个数是多少? (2)0.15除以的商加上5,再乘以,积是多少? 23.(4分)(2012•富源县)车队向灾区运送一批救灾物资,去时每小时行80km,5小时到达灾区.回来时每小时行100km,这支车队要多长时间能够返回出发地? 24.(4分)(2012•富源县)书店有一套科普丛书原价96元,现按6折出售,买一套可以便宜多少元?如果买6套,360元钱够吗? 25.(4分)(2012•晋城)邮局汇款的汇率是1%,在外打工的小明的爸爸给家里汇钱,一共交了38元的汇费,小明的爸爸一共给家里汇了多少元? 26.(4分)(2012•富源县)汽车厂计划25天组装汽车4000辆,实际提前5天完成,实际平均每天组装汽车多少辆? 27.(4分)(2012•平坝县)一个长方体玻璃鱼缸(鱼缸的上面没有玻璃),长5分米,宽3分米,高3.5分米.制作这个鱼缸至少需要多少平方分米的玻璃? 28.(5分)(2012•富源县)求如图阴影部分的面积.单位:米 (π取3.14) 29.(5分)(2012•富源县)一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?(π取3.14) 30.(11分)(2010•桃源县模拟)下面是某数码照相机厂 2006﹣﹣2009年两种型号照相机产量统计表. 单位:万台 型号 年份 2006年 2007年 2008年 2009年 甲种照相机 15 23 30 40 乙种照相机 10 18 25 45 根据表中的数据,完成下面统计图 (1)完成上面统计图. (2)哪种照相机增长的较快? (3)2009年乙种相机是甲种相机的几分之几? (4)2006年到2009年甲种相机的平均年产量是多少万台? 参考答案 1.1 9002 0400,2亿. 【解析】 试题分析:最小的奇数是1,最大的一位数是9,最后的质数是2,最小的合数是4,根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出此数;省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字. 解:这个数写作:1 9002 0400; 1 9002 0400≈2亿. 故答案为:1 9002 0400,2亿. 点评:本题主要考查整数的写法、改写和求近似数.注意,改写和求近似数时要带计数单位.关键是根据奇数与偶数的意义、质数与合数的意义,自然数的意义确定每位上的数字. 2.反,5:3. 【解析】 试题分析:(1)要想判定两个相关联的量之间成什么比例关系,必须根据式子,进行推导,看看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例; (2)逆用比例的基本性质解答,即在比例里,两个内项的积等于两个外项的积. 解:(1)n=, mn=3(一定), 符合反比例的意义, 所以m与n成反比例; (2)a×3=b×5, a:b=5:3; 故答案为:反,5:3. 点评:此题是考查利用正、反比例的意义来辨识成正比例的量和成反比例的量,以及灵活利用比例的基本性质解决问题. 3.48. 【解析】 试题分析:“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒,从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒,由此即可解答. 解:“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒, 从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒, 故答案为:48. 点评:爬的层数=楼层数之差,由此即可解答此类问题. 4.4,18,16,7.5. 【解析】 试题分析:解决此题关键在于75%,75%可改成折数7.5折,75%可改写成分数,的分母相当于被除数写成3÷4;的分母从4到24扩大6倍,3也扩大6倍是18;的分子从3到12扩大4倍,4也扩大4倍是16.据此进行改写即可 解:3÷4=18÷24==75%=7.5折. 故答案为:4,18,16,7.5. 点评:此题考查分数、小数、百分数和折数间的互化,根据它们之间的关系和性质进行改写即可. 5.4厘米,80π平方厘米,160π立方厘米. 【解析】 试题分析:(1)根据“r=d÷2”解答即可; (2)根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:求长方形的面积,即圆柱的侧面积,根据“圆柱的侧面积=πdh“解答即可; (3)求圆柱的体积,根据圆柱体积=πr2h解答即可. 解:(1)8÷2=4(厘米); (2)π×8×10, =π×80, =80π(平方厘米); (3)π×42×10, =160π(立方厘米); 故答案为:4厘米,80π平方厘米,160π立方厘米. 点评:此题考查了圆柱的侧面展开图,以及圆柱的侧面积、圆柱的体积计算方法的应用. 6.5. 【解析】 试题分析:根据“1千克盐水中含盐50克”,可知盐水中盐的质量是50克,盐水的质量是1000克,进而用盐的质量除以盐水的质量即可. 解:50÷1000=0.05=5%. 答:盐是盐水的5%. 故答案为:5. 点评:此题考查百分数的实际应用:求一个数是另一个数的百分之几,用除法计算. 7.25. 【解析】 试题分析:假设男生有4人,则女生有5人,求女学生比男学生人数多百分之几,把男生人数看作单位“1”,根据“(大数﹣小数)÷单位“1”的量”进行解答即可. 解:(5﹣4)÷4, =1÷4, =25%; 故答案为:25. 点评:解答此题的关键是先进行假设,进而判断出单位“1”,根据“(大数﹣小数)÷单位“1”的量”进行解答. 8.1:300000. 【解析】 试题分析:根据比例尺的意义知道,图上距离与实际距离的比就是比例尺,由此先把实际距离30千米换算成以厘米做单位,再写出对应比,化简即可. 解:因为,30km=3000000cm, 所以,10cm:3000000cm=1:300000; 故答案为:1:300000. 点评:此题主要考查了比例尺的意义,另外注意图上距离与实际距离的单位要统一;比例尺是一个比,不能带单位. 9.错误 【解析】 试题分析:举出一个反例,自然数(0除外)中有既不是质数也不是合数的数,进行证明. 解:自然数1既不是质数也不是合数,所以自然数(0除外)不是质数,就是合数的说法是错误的. 故答案为:错误. 点评:本题主要考查质数合数的意义,注意自然数1既不是质数也不是合数. 10.错误 【解析】 试题分析:利用分数的基本性质,把这两个数的分子、分母分别扩大即可判断得出. 解:根据分数的基本性质,分子、分母分别扩大相同的倍数后,得到的分数就有无数个, =,=,两数之间就还有以及, 在扩大不同的倍数后,还有无数个. 所以原判断是错误的. 故答案为:×. 点评:本题主要考查学生对于分数的基本性质的灵活应用. 11.正确 【解析】 试题分析:等底等高的圆柱的体积是圆锥的体积的3倍,已知他们的体积和是36立方米,则圆锥的体积是体积之和的,由此计算得出圆锥的体积进行判断. 解:圆锥的体积是:36×=9(立方米); 所以原题说法正确. 故答案为:正确. 点评:此题考查了等底等高的圆柱与圆锥体积的倍数关系的灵活应用. 12.错误 【解析】 试题分析:首先理解合格率,合格率是指合格产品的个数占产品总个数的百分之几,进而用:×100%=合格率,由此列式解答后再判断. 解:合格产品的个数:90﹣10=80(个), 合格率:×100%≈0.889=88.9%; 答:合格率是88.9%. 故答案为:错误. 点评:此题属于考查求百分率的应用题,应用的等量关系式是:×100%=合格率. 13.正确 【解析】 试题分析:判断两种量成不成比例,成什么比例,就看这两种量是否是①相关联;②一种量变化,另一种量也随着变化,变化方向相同或相反;③对应的比值或乘积一定;如果这两种量相关联的量都是变量,且对应的比值一定,就成正比例;如果两种量相关联的量都是变量,且对应的乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例. 解:因为青蛙的腿的条数:只数=4:1=8:2=4(一定),是青蛙的腿的条数与只数对应的比值一定, 所以青蛙的只数与腿的条数成正比例关系; 故判断为:正确. 点评:此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断. 14.C 【解析】 试题分析:判定一下2008是不是闰年,判定闰年的办法:年份是4的倍数的就是闰年,否则不是闰年,整百年必需是400的倍数,1月、3月是大月有31天,二月闰年29天,平年28天,然后把时间加起来即可. 解:2008是4的倍数,2008是闰年; 所以2008年的1月份、2月份、3月份一共有:31+29+31=91(天); 故选:C. 点评:本题主要考查判定闰年的办法,年份是4的倍数的就是闰年,否则不是闰年,整百年必需是400的倍数. 15.A 【解析】 试题分析:根据梯形高的定义知,梯形是只有一组对边平形的四边形,梯形的高是指上底和下底之间的距离,把长方形任意分割成两个梯形时,两平行线之间距离是相等的,据此可判断. 解:根据以上分析,把一个长方形任意分割成两个梯形,其中的高一定相等. 故选:A. 点评:此题是考查平行四边形的特征,平行四边形是两组对边平行,它们之间的距离总是相等;由此求解. 16.C 【解析】 试题分析:据题意5﹣3表示宽比长少的数量,除以5表示宽比长少的数量占长的几分之几. 解:表示宽比长少的占长的几分之几. 故选:C. 点评:此题考查分数应用题的基本类型:一个数比另一个多(或)几分之几的数,多的(或少的)除以另一个数. 17.C 【解析】 试题分析:分子缩小,分母扩大,只要把它们扩大或缩小的倍数相乘,算出结果即可. 解:分子缩小3倍,分母扩大3倍, 可以看做分子不变,分母扩大9倍, 即:3×3=9,分子不变,分母扩大9倍, 也就是这个分数的分数值缩小了9倍. 故选:C. 点评:本题主要考查学生对于分数基本性质的理解. 18.D 【解析】 试题分析:判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例.据此进行判断并选择. 解:A、因为y=3+x,所以y﹣x=3(一定),是x和y的差一定,x和y不成比例; B、因为x+y=(一定),是X和Y的和一定,x和y不成比例; C、因为x=,所以x÷y=(一定),是比值一定,x和y成正比例; D、因为y=所以xy=1,是乘积一定,x和y成反比例; 故选:D. 点评:此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择. 19.1300;5;9.14;18;;10;6;10;5;;;3.5; 【解析】 试题分析:根据四则运算的计算法则计算即可求解.其中12×(+)根据乘法分配律简便计算,2.5×3.5×0.4根据乘法交换律和结合律简便计算. 解: 26×50=1300 25×0.2=5 10﹣0.86=9.14 24×=18 ÷3= 125%×8=10 4.8÷0.8=6 8÷=10 12×(+)=5 1﹣1÷9= ×0= 2.5×3.5×0.4=3.5 点评:考查了四则运算,关键是熟练掌握计算法则正确进行计算. 20.20.025;8.6;42. 【解析】 试题分析:(1)先算乘法,再算加法; (2)先算除法和乘法,再根据减法的性质进行简算; (3)根据乘法分配律进行简算. 解:(1)25×+2.5% =20+2.5% =20.025; (2)9.6﹣11÷7+×4 =9.6﹣+ =9.6﹣(﹣) =9.6﹣1 =8.6; (3)12×[(﹣)×3] =12×[×3﹣×3] =12×[﹣2] =12×﹣12×2 =66﹣24 =42. 点评:考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律简便计算. 21.(1)1.6;(2)4;(3)19.2. 【解析】 试题分析:(1)根据等式的性质,方程的两边同时减去5.4,然后再同除以2,即可解答; (2)先根据比例的性质改写成5x=2.5×8,再根据等式的性质,两边同除以5,即可解答; (3)根据等式的性质,方程的两端同时加上x;然后再同时减去0.2,最后方程的两边再同乘24,即可解答. 解:(1)5.4+2x=8.6, 5.4+2x﹣5.4=8.6﹣5.4, 2x=3.2, 2x÷2=3.2÷2, x=1.6; (2)2.5:5=x:8, 5x=2.5×8, 5x=20, 5x÷5=20÷5, x=4; (3)0.2=1﹣, 0.2+=1﹣+, 0.2+=1, 0.2+﹣0.2=1﹣0.2, =0.8, ×24=0.8×24, x=19.2. 点评:本题考查的知识点是:比例的基本性质即“两项之积等于两外项之积”,等式的基本性质,即:“方程两边同时加上、或减去、或乘上、或除以同一个不等于0的数,左右两边仍然相等”;注意等号上下要对齐. 22.(1)340;(2)1.35. 【解析】 试题分析:(1)180比一个数的50%多10,即180减去10正好是这个数的50%,求这个数用除法:(180﹣10)÷50%; (2)0.15除以的商为0.15,其加上5的和为0.15+5,所以0.15除以的商加上5,再乘以,积是:(0.15+5)×. 解:(1)(180﹣10)÷50%, =170÷50%, =340; 答:这个数是340. (2)(0.15+5)× =(0.4+5)×, =5.4×, =1.35. 答:积是1.35. 点评:在完成列式计题目时,要注意题目中“加上、减去、除以、乘、再”等体现运算符号及运算顺序的词语. 23.4小时. 【解析】 试题分析:要求这支车队要多长时间能够返回出发地,根据时间=路程÷速度,速度已知是每小时行100km,只要求出路程就可,因来回路程是一样的,去时的速度是每小时行80km,时间是5小时,所此可解答. 解:80×5÷100, =400÷100, =4(小时). 答:这支车队要4小时能够返回出发地. 点评:本题重点考查学生对速度、路程、时间三者之间的关系的掌握情况. 24.买一套可以便宜38.4元,如果买6套,360元钱够. 【解析】 试题分析:6折是指现价是原价的60%,把原价看成单位“1”,用原价乘上60%就是一套的现价是多少元,进而求出便宜了多少钱?然后用一套的现价乘上6,求出6套的现价,再与360元比较即可求解. 解:96×60%=57.6(元); 96﹣57.6=38.4(元); 57.6×6=345.6(元); 345<360; 答:买一套可以便宜38.4元,如果买6套,360元钱够. 点评:本题关键是理解打折的含义:打几折,现价就是原价的百分之几十. 25.3800元. 【解析】 试题分析:理解汇率,汇率是指汇费占汇款总数的百分之几,汇率=×100%,得出汇款总数=汇费÷汇率,就此计算即可. 解:38÷1%, =38÷0.01, =3800(元). 答:小明的爸爸一共给家里汇了3800元. 点评:此题属于百分率问题,解决此题关键是根据求汇率的计算方法,推出求汇款总数的方法:汇费除以汇率. 26.200辆 【解析】 试题分析:计划25天完成,实际提前5天完成,即实际工作25﹣5=20天就完成了任务,求平均每天组装汽车多少辆,用除法. 解:4000÷(25﹣5), =4000÷20, =200(辆). 答:实际平均每天组装汽车200辆. 点评:本题考查了学生完成简单的整数除法应用题的能力. 27.71平方分米 【解析】 试题分析:要求制作这个鱼缸至少需要多少平方分米的玻璃,也就是求长方体五个面的面积(缺少上面),由此即可列式解答. 解:5×3+(5×3.5+3×3.5)×2; =15+(17.5+10.5)×2; =15+56; =71(平方分米); 答:制作这个鱼缸至少需要71平方分米的玻璃. 点评:此题是长方体表面积的实际应用,关键要弄清是求哪几个面的面积,缺少哪个面,然后列式解答即可. 28.343平方米 【解析】 试题分析:观察图形可得:阴影部分的面积等于长为25米,宽为20米的长方形的面积与直径为20米的半圆的面积之差. 解:25×20﹣3.14×÷2, =500﹣157, =343(平方米); 答:阴影部分的面积是343平方米. 点评:把阴影部分的面积转化成规则图形长方形和圆的面积中进行计算是解决本题的关键. 29.18.84平方厘米. 【解析】 试题分析:圆锥铅锤的体积等于圆柱容器水面下降的那部分水的体积,先根据圆柱的体积公式,求出容器中水下降的体积(即圆锥的体积),已知圆锥的高是9厘米,用体积除以高再除以即可求出底面积.由此列式解答. 解:容器水下降的体积: 3.14×62×0.5 =3.14×36×0.5 =56.52(立方厘米); 圆锥的底面积: 56.52÷(×9) =56.52÷3 =18.84(平方厘米); 答:这个圆锥体的底面积是18.84平方厘米. 点评:此题解答关键是理解容器中水下降的那部分水的体积等于圆锥的体积,利用圆柱、圆锥的体积计算方法解决问题. 30.(1)统计图见下图: (2)从统计图中,可看出乙种照相机增长的较快; (3)2009年乙种相机是甲种相机的; (4)27万台. 【解析】 试题分析:(1)先根据统计表中的数据,完成复式折线统计图; (2)直观观察统计图中的折线,确定哪种照相机增长的较快; (3)就是求45是40的几分之几,用除法计算; (4)用2006年到2009年甲种相机的总万台数除以年数即可解决. 解:(1)统计图见下图: (2)从统计图中,可看出乙种照相机增长的较快; 答:乙种照相机增长的较快. (3)2009年乙种相机是甲种相机的:45÷40==; 答:2009年乙种相机是甲种相机的. (4)2006年到2009年甲种相机的平均年产量: (15+23+30+40)÷4, =108÷4, =27(万台); 答:2006年到2009年甲种相机的平均年产量是27万台. 点评:此题考查根据统计表中的信息,绘制成复式折线统计图,再根据统计图解决一些实际问题即可.查看更多