实际问题与一元二次方程（3）　　导学案

实际问题与一元二次方程（3）　　导学案

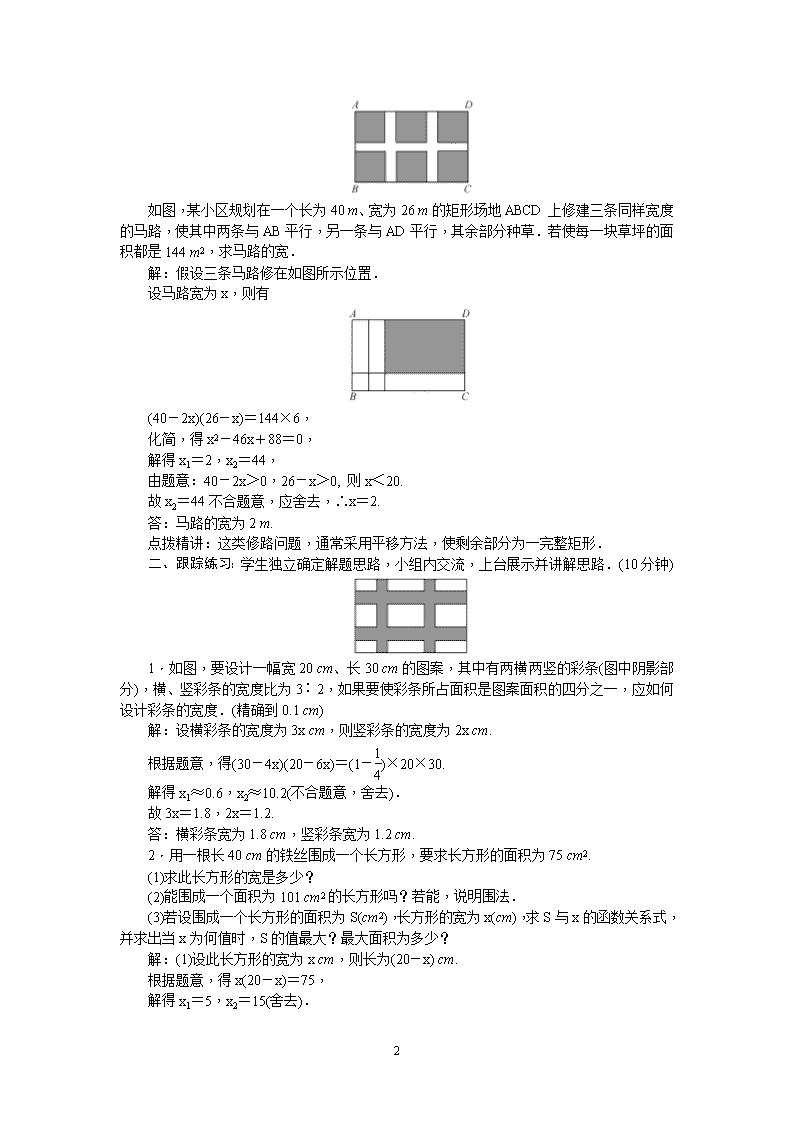
‎21.3　实际问题与一元二次方程(3)‎ ‎1. 能根据具体问题中的数量关系，列出一元二次方程，体会方程是刻画现实世界的一个有效的数学模型．并能根据具体问题的实际意义，检验结果是否合理．‎ ‎2. 列一元二次方程解有关特殊图形问题的应用题．‎ 重点：根据面积与面积之间的等量关系建立一元二次方程的数学模型并运用它解决实际问题．‎ 难点：根据面积与面积之间的等量关系建立一元二次方程的数学模型．‎ 一、自学指导．(10分钟)‎ 问题：如图，要设计一本书的封面，封面长27 cm，宽21 cm，正中央是一个与整个封面长宽比例相同的矩形．如果要使四周的阴影边衬所占面积 是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度？(精确到0.1 cm)‎ 分析：封面的长宽之比是27∶21＝__9∶7，中央的长方形的长宽之比也应是__9∶7__，若设中央的长方形的长和宽分别是__9a_cm__和__7a_cm__，由此得上下边衬与左右边衬的宽度之比是__(27－9a)∶(21－7a)＝9∶7__．‎ 探究：怎样设未知数可以更简单的解决上面的问题？请试一试．‎ 二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(5分钟)‎ 在一幅长8分米，宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边，制成一幅矩形挂图(如图②)．如果要使整个挂图的面积是80平方分米，求金色纸边的宽．‎ ‎　解：设金色纸边的宽为x分米，根据题意，得(2x＋6)(2x＋8)＝80.‎ ‎ 　解得x1＝1，x2＝－8(不合题意，舍去)．‎ ‎　答：金色纸边的宽为1分米．‎ ‎ 点拨精讲：本题和上题一样，利用矩形的面积公式做为相等关系列方程．‎ 一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(8分钟)‎ 3‎ 如图，某小区规划在一个长为40 m、宽为26 m的矩形场地ABCD上修建三条同样宽度的马路，使其中两条与AB平行，另一条与AD平行，其余部分种草．若使每一块草坪的面积都是144 m2，求马路的宽．‎ 解：假设三条马路修在如图所示位置．‎ 设马路宽为x，则有 ‎(40－2x)(26－x)＝144×6，‎ 化简，得x2－46x＋88＝0，‎ 解得x1＝2，x2＝44，‎ 由题意：40－2x＞0，26－x＞0, 则x＜20.‎ 故x2＝44不合题意，应舍去，∴x＝2.‎ 答：马路的宽为2 m.‎ 点拨精讲：这类修路问题，通常采用平移方法，使剩余部分为一完整矩形．‎ 二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(10分钟)‎ ‎1．如图，要设计一幅宽20 cm、长30 cm的图案，其中有两横两竖的彩条(图中阴影部分)，横、竖彩条的宽度比为3∶2，如果要使彩条所占面积是图案面积的四分之一，应如何设计彩条的宽度．(精确到0.1 cm)‎ 解：设横彩条的宽度为3x cm，则竖彩条的宽度为2x cm.‎ 根据题意，得(30－4x)(20－6x)＝(1－)×20×30.‎ 解得x1≈0.6，x2≈10.2(不合题意，舍去)．‎ 故3x＝1.8，2x＝1.2.‎ 答：横彩条宽为1.8 cm，竖彩条宽为1.2 cm.‎ ‎2．用一根长40 cm的铁丝围成一个长方形，要求长方形的面积为75 cm2.‎ ‎(1)求此长方形的宽是多少？‎ ‎(2)能围成一个面积为101 cm2的长方形吗？若能，说明围法．‎ ‎(3)若设围成一个长方形的面积为S(cm2)，长方形的宽为x(cm)，求S与x的函数关系式，并求出当x为何值时，S的值最大？最大面积为多少？‎ 解：(1)设此长方形的宽为x cm，则长为(20－x) cm.‎ 根据题意，得x(20－x)＝75，‎ 解得x1＝5，x2＝15(舍去)．‎ 3‎ 答：此长方形的宽是5 cm.‎ ‎(2)不能．由x(20－x)＝101，即x2－20x＋101＝0，知Δ＝202－4×101＝－4＜0，方程无解，故不能围成一个面积为101 cm2的长方形．‎ ‎(3)S＝x(20－x)＝－x2＋20x.‎ 由S＝－x2＋20x＝－(x－10)2＋100知，当x＝10时，S的值最大，最大面积为100 cm2.‎ 点拨精讲：注意一元二次方程根的判别式和配方法在第(2)(3)问中的应用．‎ 学生总结本堂课的收获与困惑．(2分钟)‎ 用一元二次方程解决特殊图形问题时，通常要先画出图形，利用图形的面积找相等关系列方程．‎ 学习至此，请使用本课时对应训练部分．(10分钟)‎ 3‎