- 2021-04-22 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广州市 2020 届高三年级阶段训练题数学(文科)试题
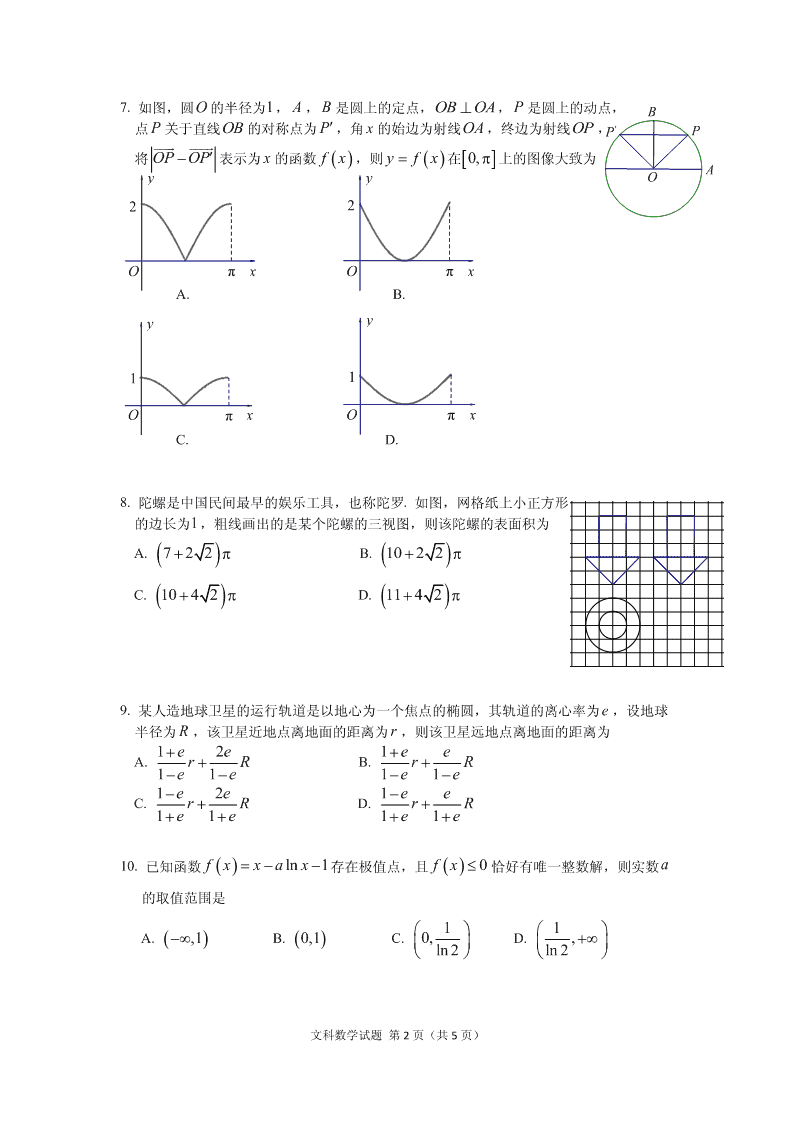
文科数学试题 第 1 页(共 5 页) 秘密★启用前 试卷类型:B 广州市 2020 届高三年级阶段训练题 文科数学 本试卷共 5 页,23 小题,满分 150 分。考试用时 120 分钟。 注意事项: 1.答卷前,考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡上,并用 2B 铅笔在答题卡的相应位置填涂考生号,并将试卷类型(B)填涂在答题卡相应位置上。 2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息 点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。写在本试卷上无效。 3.作答填空题和解答题时,必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题 卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案; 不准使用铅笔和涂改液。不按以上要求作答无效。 4.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。 一、选择题:本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有 一项是符合题目要求的. 1. 已知复数 z i 1i ,则 z A. 1 2 B. 2 2 C. 1 D. 2 2. 已知集合 0,1,2,3A , 1,0,1B , P A B ,则 P 的子集共有 A. 2 个 B. 4 个 C. 6 个 D. 8 个 3. 设向量a ,1 m , b 2, 1,且 ab,则 m A. 2 B. 1 2 C. 1 2 D. 2 4. 已知 na 是等差数列, 3 5a , 2 4 6 7a a a ,则数列 的公差为 A. 2 B. 1 C. 1 D. 2 5. 已知命题 p : xR, 2 10xx ;命题 q : xR, 23xx ,则下列命题中为真 命题的是 A. pq B. pq C. pq D. pq 6. 已知偶函数 fx满足 2 0f x x xx ,则 21x f x A. 4xx 或 0x B. 0xx 或 4x C. 2xx 或 2x D. 或 4x 文科数学试题 第 2 页(共 5 页) P' B P O A 2 O π x y 1 O π x y 2 O π x y 1 O π x y 7. 如图,圆O 的半径为1, A , B 是圆上的定点,OB OA , P 是圆上的动点, 点 P 关于直线OB 的对称点为 P,角 x 的始边为射线OA,终边为射线OP , 将 OP OP 表示为 x 的函数 fx,则 y f x 在 0, 上的图像大致为 A. B. C. D. 8. 陀螺是中国民间最早的娱乐工具,也称陀罗. 如图,网格纸上小正方形 的边长为1,粗线画出的是某个陀螺的三视图,则该陀螺的表面积为 A. 7 2 2 B. 10 2 2 C. 10 4 2 D. 11 4 2 9. 某人造地球卫星的运行轨道是以地心为一个焦点的椭圆,其轨道的离心率为 e ,设地球 半径为 R ,该卫星近地点离地面的距离为 r ,则该卫星远地点离地面的距离为 A. 12 11 eerRee B. 1 11 eerRee C. 12 11 eerRee D. 1 11 eerRee 10. 已知函数 ln 1f x x a x 存在极值点,且 0fx 恰好有唯一整数解,则实数 a 的取值范围是 A. ,1 B. 0,1 C. 10, ln 2 D. 1 ,ln 2 文科数学试题 第 3 页(共 5 页) 11. 已知 1F , 2F 是双曲线 2 2 2:1xCya 0a 的两个焦点,过点 1F 且垂直于 x 轴的直线 与C 相交于 A , B 两点,若 2AB ,则△ 2ABF 的内切圆的半径为 A. 2 3 B. 3 3 C. 22 3 D. 23 3 12. 已知正方体 1 1 1 1ABCD A B C D 的棱长为 2 ,E ,F ,G 分别是棱 AD , 1CC , 11CD的 中点,给出下列四个命题: ① 1EF B C ; ② 直线 FG 与直线 1AD所成角为 60 ; ③ 过 , , 三点的平面截该正方体所得的截面为六边形; ④ 三棱锥 B EFG 的体积为 5 6 . 其中,正确命题的个数为 A. 1 B. 2 C. 3 D. 4 二、填空题:本题共 4 小题,每小题 5 分,共 20 分. 13. 已知函数 y f x 的图像与 2xy 的图像关于直线 yx 对称,则 4f . 14. 设 x , y 满足约束条件 1 3, 0 2, x xy 则 2z x y 的最小值为 . 15. 羽毛球混合双打比赛每队由一男一女两名运动员组成. 某班级从3 名男生 1A , 2A , 3A 和 3 名女生 1B , 2B , 3B 中各随机选出两名,把选出的 4 人随机分成两队进行羽毛球混合 双打比赛,则 1A 和 1B 两人组成一队参加比赛的概率为 . 16. 记 nS 为数列 na 的前 n 项和,若 1 12 2nn nSa ,则 34aa , 数列 2nnaa 的前 n 项和 nT . (第 1 空 2 分,第 2 空 3 分) 文科数学试题 第 4 页(共 5 页) C B A P 62.0 62.5 63.0 63.5 64.0 64.5 65.0 0.075 0.100 0.200 0.225 0.650 零件尺寸/mm 0.750 频率 组距 三、解答题: 共 70 分.解答应写出文字说明、证明过程和演算步骤.第 17~21 题为必考 题,每个试题考生都必须做答. 第 22、23 题为选考题,考生根据要求做答. (一)必考题:共 60 分. 17.(12 分) 某企业质量检验员为了检测生产线上零件的情况,从生产线上随机抽取了80 个零件进行测 量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图: (1)根据频率分布直方图,求这80 个零件尺寸的中位数(结果精确到 0.01); (2)已知尺寸在 63.0,64.5 上的零件为一等品,否则为二等品. 将这 个零件尺寸的样 本频率视为概率,从生产线上随机抽取1个零件,试估计所抽取的零件是二等品的概率. 18.(12 分) 已知 ,,abc分别是△ ABC 内角 ,,A B C 的对边, 2 2 22sin sin sin sin sin3 A C A C B . (1)求sin B 的值; (2)若 2b ,△ 的面积为 2 ,求△ 的周长. 19.(12 分) 如图,三棱锥 P ABC 中, PA PC , AB BC , 120APC , 90ABC , 32AC PB. (1)求证: AC PB ; (2)求点C 到平面 PAB 的距离. 文科数学试题 第 5 页(共 5 页) 20. (12 分) 已知点 P 是抛物线 21:34C y x的顶点, A , B 是C 上的两个动点,且 4PA PB . (1)判断点 0, 1D 是否在直线 AB 上?说明理由; (2)设点 M 是△ PAB 的外接圆的圆心,求点 M 的轨迹方程. 21. (12 分) 已知函数 eln xbf x a x x,曲线 y f x 在点 1, 1f 处的切线方程为 22xy e0 . (1)求 a ,b 的值; (2)证明函数 fx存在唯一的极大值点 0x ,且 0 2ln 2 2fx . (二)选考题: 共 10 分. 请考生在第 22、23 题中任选一题作答. 如果多做,则按所做的 第一题计分. 22. [选修 4-4:坐标系与参数方程](10 分) 已知曲线 1C 的参数方程为 cos , (1 sin , xt tyt 为参数 ) , 曲线 2C 的参数方程为 sin , ( 1 cos 2 , x y 为参数). (1)求 1C 与 2C 的普通方程; (2)若 与 相交于 A , B 两点,且 2AB ,求sin 的值. 23. [选修 4-5:不等式选讲](10 分) 已知 0a , 0b ,且 1ab. (1)求 12 ab 的最小值; (2)证明: 22 25 12 ab b ab .查看更多