- 2021-04-21 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版小学六年级下册数学课件第六单元整理和复习 课时10
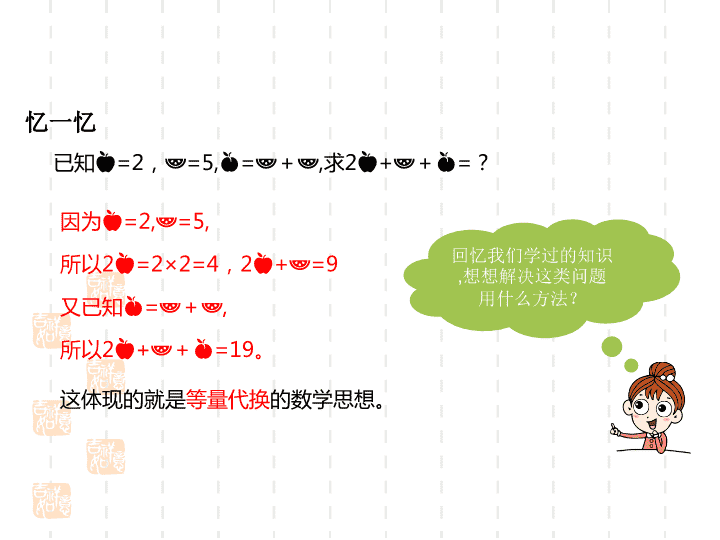
整理和复习 第10课时 数与代数 1.复习通过等量代换从而解 决实际问题的方法,复习简 单的几何证 明方法。 2.进一步发展逻辑推理能力 和解决问题的能力,体会等 量代换对解决 问题的重要性。 3. 激发学生学习数学、解 决数学问题的兴趣。提高学 生的合作意识。 § 【重点】掌握通过等量代换解决实际问题的方法。 § 【难点】能够正确的进行等量代换,能够正确的进行逻辑推理。 忆一忆 已知 =2, =5, = + ,求2 + + =? 回忆我们学过的知识, 想想解决这类问题用 什么方法? 因为 =2, =5, 所以2 =2×2=4,2 + =9 又已知 = + , 所以2 + + =19。 这体现的就是等量代换的数学思想。 各代表一个数。、 、 、 、 + =(1)已知 24, = + + 。求 和 的值。 一个 等于三个 的和。 把 + =24中的 换成 + + , 这叫等量代换。 Ø 用等量代换解决实际问题 p 例1 + = 24 + = 24+ + 等量代换 = 6 = + + =18 4× = 24 代 换 是否等于 ? + =160, + =160。已知 两个等式里都 有 ☆,可以利 用等式的性质。 根据等式的性质,等式两边都减去☆。 可以推出○=160-☆, ⦾ =160-☆ 。 因为☆代表同一个数,所以○= ⦾ 。 + =160 + =160 = 160 - = 160 - = p 例2 如右图,两条直线相交于点O。 (1)每相邻两个角可以组成一个平角,一共能 组成几个平角? ∠1和∠2, ∠ 2和∠3,∠3和∠4,∠4和 ∠1,一共能组成4个平角。 平角的两边在 一条直线上。 (2)你能推出∠1=∠3吗? 如右图,两条直线相交于点O。 ①根据第(1)题的结论,可以得到 ∠1+∠2=180°,∠2+∠3=180°。 ②根据等式的性质,等式的两边都减去∠2,可以 得到∠1=180°-∠2,∠3=180°-∠2。 ③因为180°-∠2=180°-∠2,所以∠1=∠3。 ∠1和∠2,,2和∠3,都能组成平角。 这就是等量代 换。 1 根据下面的已知条件,求○、□、△的值。 (1) ○+□=91 △+□=63 △+○=46 ○=37 □=54 △=9 (2) □-○=8 □+○=12 △=□+□+○ ○=2 □=10 △=22 (2)○+□=31 △+○=20 □+△=39 ○=( ) △=( ) □=( ) (1)○+△=150 ○= 4×△ ○=( ) △=( )120 30 6 14 25 2 求图形代表的数。 +已知 =114,+ + + + =63+ 求 、 的值。 + =63+ + =114,+ + + 3 × =63 =21 3 × +42 =114 3 × =72 =24 3 所以10+ =15 + =10 因为 + + =15 =5 因为 + =12 所以 =7 因为 + =10 所以 =3 求 、 、 的值。+ =10, + =12, + + =15。 4 如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。 因为∠1+∠5=180°, ∠1=30° 所以∠5=180° -∠1 =180° -30° =150° 5 因为∠4+∠5=180°, ∠5=150° 所以∠4=180° -∠5 =180° -150° =30° 如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。5 因为∠3+∠2+∠4=180°, ∠4=30° ,∠2=50° 所以∠3=180° -∠4-∠2 =180° -30°-50° =100° 如图中∠1=30°,∠2=50°,求∠3、∠4、∠5的度数。5 如图,把三角形ABC的边BC延长到点D。 (1)∠3和∠4拼成的是什么角?(2)你能说∠1+∠2=∠4吗? (1)∠3和∠4拼成的是平角。 (2)因为∠1+∠2+∠3=180° ∠3+∠4=180° 所以∠1+∠2+∠3=∠3+∠4 两边都减去∠3,可以得到: ∠1+∠2=∠4 6查看更多