5.1圆的有关概念与性质五年中考荟萃

5.1圆的有关概念与性质五年中考荟萃

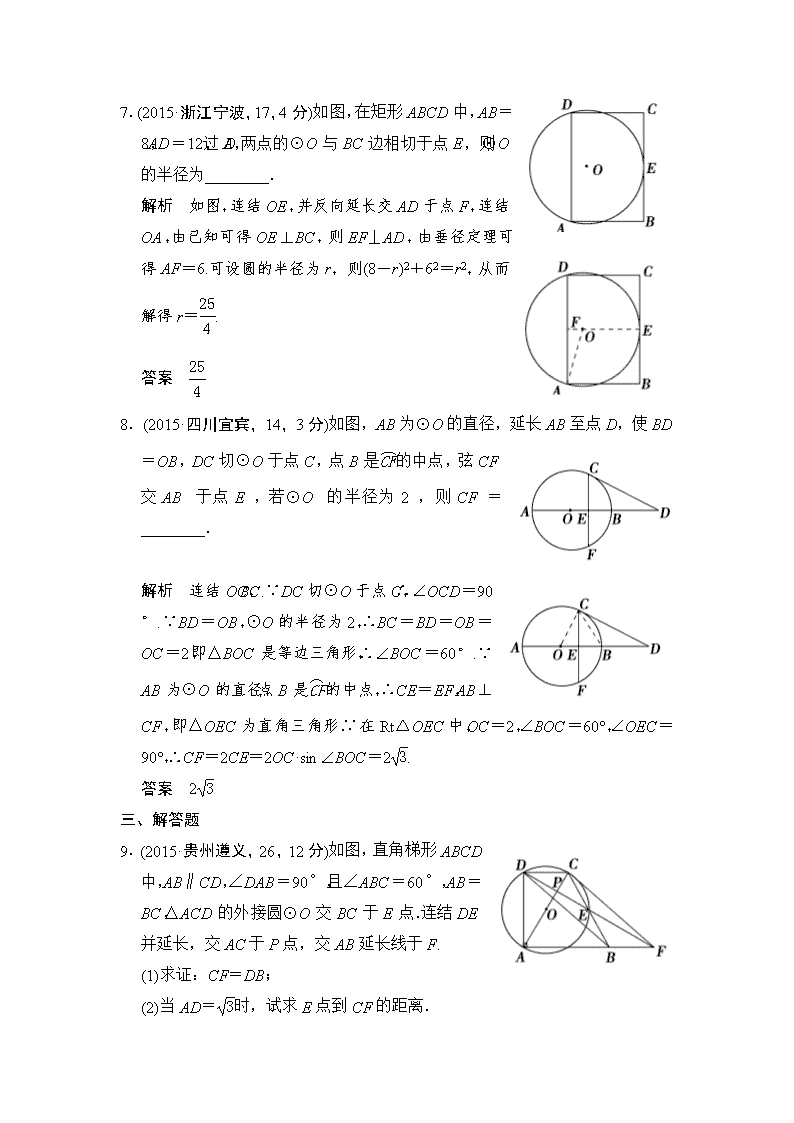
第五章 圆 §5.1 圆的有关概念与性质 A 组 2015 年全国中考题组 一、选择题 1．(2015·浙江杭州，5，3 分)圆内接四边形 ABCD 中，已知∠A＝70°，则∠C ＝ ( ) A．20° B．30° C．70° D．110° 解析 根据圆内接四边形的对角互补可得． 答案 D 2．(2015·浙江衢州，7，3 分)数学课上，老师让学生尺规 作图画 Rt△ABC，使其斜边 AB＝c，一条直角边 BC＝ a.小明的作法如图所示，你认为这种作法中判断∠ACB 是直角的依据是 ( ) A．勾股定理 B．直径所对的圆周角是直角 C．勾股定理的逆定理 D．90°的圆周角所对的弦是直径 解析 由于作图构造的是以 AB 为直径的圆，故选 B. 答案 B 3．(2015·福建福州，8，3 分)如图，C，D 分别是线段 AB，AC 的中点，分别以 点 C，D 为圆心，BC 长为半径画弧，两弧交于点 M，测量∠AMB 的度数， 结果为 ( ) A．80° B．90° C．100° D．105° 解析 由于点 M 在以 C 为圆心 BC 为半径的圆上，故∠AMB 为直径所对的圆 周角，是直角． 答案 B 4．(2015·四川巴中，9，3 分)如图，在⊙O 中，弦 AC∥ 半径 OB，∠BOC＝50°，则∠OAB 的度数为( ) A．25° B．50° C．60° D．30° 解析 ∵弦 AC∥半径 OB，∴∠C＝∠BOC＝50°， ∴∠AOC＝80°，∴∠AOB＝80°＋50°＝130°.∵OA＝OB，∴∠OAB＝ 25°. 答案 A 5．(2015·山东泰安，9，3 分)如图，⊙O 是△ABC 的外接 圆，∠B＝60°，⊙O 的半径为 4，则 AC 的长等于( ) A．4 3 B．6 3 C．2 3 D．8 解 析 如 图 ， 连 结 OA ， OC ， 作 OD⊥AC 于 点 D.∵∠AOC＝2∠B＝120°，又∵OA＝OC，∴∠OAD ＝30°，∴OD＝1 2OA＝2，∴AD＝ 42－22＝2 3.再 由垂径定理可得 AC＝2AD＝4 3. 答案 A 二、填空题 6．(2015·浙江丽水，13，4 分)如图，圆心角∠AOB＝20°， 将AB ︵旋转 n°得到CD ︵ ，则CD ︵ 的度数是________度． 解析 根据在同圆或等圆中，同弧或等弧所对的圆心 角相等． 答案 20° 7．(2015·浙江宁波，17，4 分)如图，在矩形 ABCD 中， AB＝8，AD＝12，过 A，D 两点的⊙O 与 BC 边相切于 点 E，则⊙O 的半径为________． 解析 如图，连结 OE，并反向延长交 AD 于点 F，连 结 OA，由已知可得 OE⊥BC，则 EF⊥AD，由垂径定 理可得 AF＝6.可设圆的半径为 r，则(8－r)2＋62＝r2， 从而解得 r＝25 4 . 答案 25 4 8．(2015·四川宜宾，14，3 分)如图，AB 为⊙O 的直径， 延长 AB 至点 D，使 BD＝OB，DC 切⊙O 于点 C， 点 B 是CF ︵的中点，弦 CF 交 AB 于点 E，若⊙O 的半 径为 2，则 CF＝________． 解析 连结 OC，BC.∵DC 切⊙O 于点 C，∴∠OCD ＝90°.∵BD＝OB，⊙O 的半径为 2，∴BC＝BD＝ OB＝OC＝2，即△BOC 是等边三角形，∴∠BOC ＝60°.∵AB 为⊙O 的直径，点 B 是CF ︵的中点，∴ CE＝EF，AB⊥CF，即△OEC 为直角三角形．∵在 Rt△OEC 中，OC＝2，∠ BOC＝60°，∠OEC＝90°，∴CF＝2CE＝2OC·sin∠BOC＝2 3. 答案 2 3 三、解答题 9．(2015·贵州遵义，26，12 分)如图，直角梯形 ABCD 中，AB∥CD，∠DAB＝90°，且∠ABC＝60°， AB＝BC，△ACD 的外接圆⊙O 交 BC 于 E 点．连 结 DE 并延长，交 AC 于 P 点，交 AB 延长线于 F. (1)求证：CF＝DB； (2)当 AD＝ 3时，试求 E 点到 CF 的距离． (1)证明 连结 AE. ∵BC＝AB，∠ABC＝60°， ∴△ABC 是等边三角形． ∵DC∥AB，∠DAB＝90°， ∴∠ADC＝90°， ∴AC 是⊙O 的直径， ∴∠AEC＝90°， ∴CE＝BE(三线合一)． 又∵∠1＝∠2，∠3＝∠4， ∴△DCE≌△FBE， ∴CD＝BF， ∴四边形 BFCD 是平行四边形， ∴BD＝CF. (2)解 法一 过 E 作 EG⊥CF 于 G 点． ∵△ABC 是等边三角形， ∴∠CAB＝60°，∴∠DCA＝60°， ∴∠DAC＝30°. ∵Rt△ADC 中，AD＝ 3， ∴DC＝AD·tan∠DAC＝ 3× 3 3 ＝1， AC＝2DC＝2， ∴AB＝2， ∴BD＝ 7. ∵四边形 BFCD 是平行四边形， ∴BF＝CD＝1，CF＝BD＝ 7. 又∵S△CEF＝1 4S▱BDCF， ∴1 2 ·CF·GE＝1 4BF·AD， 即1 2 × 7·GE＝1 4 ×1× 3， GE＝ 21 14 ， ∴E 点到 CF 的距离为 21 14 . 法二 作 EG⊥CF，垂足为 G， ∵∠BAD＝90°，∠BAC＝60°， ∴∠CAD＝30°. 又∵AE 是等边三角形 BC 边上的高， ∴∠CAE＝30°. ∴CD ︵ ＝CE ︵ .又 AC 是直径， ∴AC⊥DE， ∴△FEG∽△FCP， ∴EG CP ＝EF CF. ∵CP＝1 2CD＝1 2 ，EF＝DE＝ 3，CF＝DB＝ 7， ∴EG· 7＝1 2 ·3， 即 EG＝ 21 14 ， ∴E 点到 CF 的距离为 21 14 . 10．(2015·浙江宁波，26，14 分)如图，在平面直角坐标系中，点 M 是第一象限 内一点，过点 M 的直线分别交 x 轴，y 轴的正半轴于 A，B 两点，且点 M 是 AB 的中点．以 OM 为直径的⊙P 分别交 x 轴，y 轴于 C，D 两点，交直线 AB 于点 E(位于点 M 右下方)，连结 DE 交 OM 于点 K. (1)若点 M 的坐标为(3，4)， ①求 A，B 两点的坐标；②求 ME 的长； (2)若OK MK ＝3，求∠OBA 的度数； (3)设 tan∠OBA＝x(0

查看更多