广东高考文科数学近5年试题分类汇编20072011
广东高考文科数学近5年试题分类汇编
1.集合与简易逻辑
2007
2008
2009
2010
2011
5
5
5分
10分
5
(2007年高考广东卷第1小题)已知集合,则(C )
A. B. C. D.
(2008年高考广东卷第1小题)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员},集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是(D )
A. B. C. B∪C = A D. A∩B = C
(2009年高考广东卷第1小题).已知全集U=R,则正确表示集合M= {-1,0,1} 和N= { x |x+x=0} 关系的韦恩(Venn)图是
【答案】B【解析】由N= { x |x+x=0}得,选B.
(2010年高考广东卷第1小题)若集合A={0,1,2,3},B={1,2,4},则集合AB=( A.)
A.{0,1,2,3,4} B.{1,2,3,4} C.{1,2} D.{0}
(2010年高考广东卷第8小题) “>0”是“>0”成立的( A.)
A.充分非必要条件 B.必要非充分条件w_w C.非充分非必要条件 D.充要条件
(2011年高考广东卷第2小题)
已知集,则的元素个数为(C) A.4 B.3 C.2 D. 1
2.复数
2007
2008
2009
2010
2011
5
5
5
5
(2007年高考广东卷第2小题)若复数是纯虚数(是虚数单位,是实数),则( D )
A. B. C. D.2
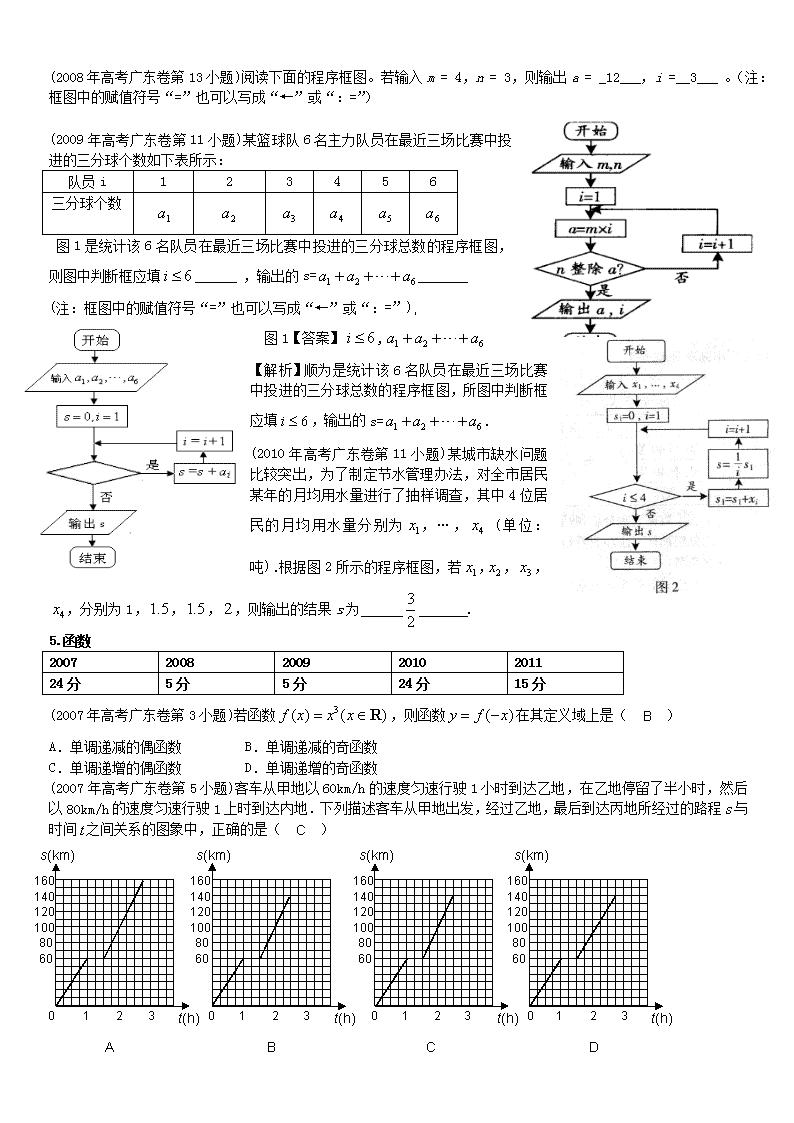
(2008年高考广东卷第2小题)已知0
-1 C. a < -1/e D. a > -1/e
(2008年高考广东卷第17小题)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560 + 48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = 购地总费用/建筑总面积)。
【解析】设楼房每平方米的平均综合费为f(x)元,则
, 令 得
当 时, ;当 时,
因此 当时,f(x)取最小值;
答:为了楼房每平方米的平均综合费最少,该楼房应建为15层。
(2009年高考广东卷第8小题)函数的单调递增区间是
A. B.(0,3) C.(1,4) D. w.w.w.k.s.5.u.c.o.m
【答案】D 【解析】,令,解得,故选D
(2009年高考广东卷第21小题)已知二次函数的导函数的图像与直线平行,且在=-1处取得最小值m-1(m).设函数
(1)若曲线上的点P到点Q(0,2)的距离的最小值为,求m的值
(2) 如何取值时,函数存在零点,并求出零点.
【解析】(1)设,则; 又的图像与直线平行
又在取极小值, , , ;
, 设
则 ;w.w.w.k.s. (2)由, 得
当时,方程有一解,函数有一零点;
当时,方程有二解,若,,
函数有两个零点;若,
,函数有两个零点;
当时,方程有一解, , 函数有一零点 (2010年高考广东卷第21小题)已知曲线,点是曲线上的点(n=1,2,…).
(1)试写出曲线在点处的切线的方程,并求出与轴的交点的坐标;
(2)若原点到的距离与线段的长度之比取得最大值,试求试点的坐标;(3)设与为两个给定的不同的正整数,与是满足(2)中条件的点的坐标,
证明:www.ks5u.com
w.w.wwww.ks5u.com
w.
w. 21.解:(1),设切线的斜率为,则
∴曲线在点处的切线的方程为:
又∵点在曲线上, ∴∴曲线在点处的切线的方程为:
即 令得,∴曲线在轴上的交点的坐标为
(2)原点到直线的距离与线段的长度之比为:
当且仅当即时,取等号。此时,故点的坐标为
(3)证法一:要证
只要证
只要证
,又
所以:
^w.k.s.5*w_w w. k#s(2011年高考广东卷第19小题) 设讨论函数
解:函数的定义域为
当的判别式
①当有两个零点,
且当内为增函数;
当内为减函数;
②当内为增函数;
③当内为增函数;
④当
在定义域内有唯一零点,
且当内为增函数;当时,内为减函数。 的单调区间如下表:
(其中)
7.三角函数与解三角形
2007
2008
2009
2010
2011
17分
17分
22分
19分
12分
(2007年高考广东卷第9小题)已知简谐运动的图象经过点,则该简谐运动的最小正周期和初相分别为( A )
A., B., C., D.,
(2007年高考广东卷第16小题)已知三个顶点的直角坐标分别为,,.
(1) 若,求的值;(2)若,求的值.
16.解: (1) , 得
(2)
(2008年高考广东卷第5小题)已知函数,,则是( D )
A. 最小正周期为π的奇函数 B. 最小正周期为π/2的奇函数
C. 最小正周期为π的偶函数 D. 最小正周期为π/2的偶函数
(2008年高考广东卷第16小题)已知函数,
的最大值是1,其图像经过点M(π/3,1/2)。(1)求的解析式;(2)已知、,且,,求的值。
16.(本小题满分13分)
已知函数的最大值是1,其图像经过点。
(1)求的解析式;(2)已知,且求的值。
【解析】(1)依题意有,则,将点代入得,而,,,故;
(2)依题意有,而,,
。
(2009年高考广东卷第7小题)已知中,的对边分别为a,b,c若a=c=且,则b=
A.2 B.4+ C.4— D.
【答案】A 【解析】由a=c=可知,,所以,由正弦定理得,故选A
(2009年高考广东卷第8小题)函数是
A.最小正周期为的奇函数 B. 最小正周期为的偶函数
C. 最小正周期为的奇函数 D. 最小正周期为的偶函数
【答案】A 【解析】因为为奇函数,,所以选A.
(2009年高考广东卷第16小题)已知向量与互相垂直,其中
(1)求和的值
(2)若,,求的值
【解析】(1),,即
又∵, ∴,即,∴
又 ,
(2) ∵
, ,即
又 , ∴ w
(2010年高考广东卷第13小题).已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=,A+C=2B,则sinA= .
设函数,,,且以为最小正周期.
(1) 求;w(2)求的解析式;(3)已知,求的值.w_w*w
16.解:(1)由已知可得:
(2)∵的周期为,即 ∴ 故
(3)∵
∴由已知得:即
∴故的值为或
(2011年高考广东卷第16小题) 已知函数
(1) 求的值;设
16.解:(1);
(2)
故
8.不等式
2007
2008
2009
2010
2011
22分
12分
10分
(2008年高考广东卷第10小题)设a、b∈R,若a - |b| > 0,则下列不等式中正确的是(D )
A. b - a > 0 B. a3 + b3 < 0 C. a2 - b2 < 0 D. b + a > 0
(2008年高考广东卷第12小题)若变量x、y满足,则的最大值是__70_____。
(2008年高考广东卷第17小题)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560 + 48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = 购地总费用/建筑总面积)。
【解析】设楼房每平方米的平均综合费为f(x)元,则
, 令 得
当 时, ;当 时,
因此 当时,f(x)取最小值;
答:为了楼房每平方米的平均综合费最少,该楼房应建为15层。
(2010年高考广东卷第19小题)
某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
x
y
O
19.解:设应当为该儿童分别预订个单位的午餐,个单位的晚餐,所花的费用为,则依题意得:
满足条件即,
目标函数为,
画出可行域如右图所示,设直线
其中为直线在轴上的截距
当直线经过直线与的交点时,取得最小值,此时取得最小值,且
由图可知,当直线经过可行域上的点M时截距最小,即
最小. 解方程组:, 得点M的坐标为 所以,22
答:要满足营养要求,并花费最少,应当为该儿童分别预订4个单位的午餐,3个单位的晚餐,此花的费用最少为22元.
(2011年高考广东卷第5小题)不等式的解积是D
A. B. C. D.
(2011年高考广东卷第6小题)已知平面直角坐标系上的区域由不等式组给定,若为上的动点,点的坐标为的最大值为B
A.3 B.4 C. D.
9.概率统计
2007
2008
2009
2010
2011
17分
18分
18分
22分
18分
(2007年高考广东卷第9小题)在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( A )
A. B. C. D.
(2007年高考广东卷第18小题)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:)
18解: (1) 散点图略
(2)
;
所求的回归方程为
(3) 当时
预测生产100吨甲产品的生产能耗比技改前降低(吨)
(2008年高考广东卷第11小题)为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在[55,75)的人数是__13_____。
(2008年高考广东卷第19小题)
某初级中学共有学生2000名,各年级男、女生人数如下表:
一年级
二年级
三年级
女生
373
x
y
男生
377
370
z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19。(1)求x的值;(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率。
19.解:(1)因为,所以
(2)初三年级人数为
现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为 名
(3)设初三年级女生比男生多的事件为,初三年级女生男生数记为 ,由(2)知,且
基本事件共有共11个,
事件包含的基本事件有
共5个,所以
(2009年高考广东卷第12小题)某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是 。若用分层抽样方法,则40岁以下年龄段应抽取 人.
图 2【答案】37, 20
【解析】由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为,则应抽取的人数为人.
(2009年高考广东卷第18小题)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
【解析】(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
=57
(3)设身高为176cm的同学被抽中的事件为A;
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173)
(181,176)(181,178) (181,179) (179,173) (179,176)
(179,178) (178,173)(178, 176) (176,173)共10个基本事件,
而事件A含有4个基本事件; ;
(2010年高考广东卷第12小题)某市居民2005~2009年家庭年平均收入x(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:w_w w. k#s5_u.c o*m
年份
2005
2006
2007
2008
2009
收入x
11.5
12.1
13
13.3
15
支出Y
6.8
8.8
9.8
10
12
根据统计资料,居民家庭年平均收入的中位数是 13 ,家庭年平均收入与年平均支出有 正 线性相关关系.
(2010年高考广东卷第17小题)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:w_w*w.k_s_5 u.c*o*m
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?w. k#s5_u.c o*m
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.w_w*w
17.解:(1)画出二维条形图,通过分析数据的图形,或者联列表的对角线的乘积的差的绝对值来分析,得到的直观印象是收看新闻节目的观众与年龄有关;
(2)在100名电视观众中,收看新闻的观众共有45人,其中20至40岁的观众有18人,大于40岁的观众共有27人。
故按分层抽样方法,在应在大于40岁的观众中中抽取人.
(3)法一:由(2)可知,抽取的5人中,年龄大于40岁的有3人,分别记作1,2,3;20岁至40岁的观众有2人,分别高为,若从5人中任取2名观众记作,则包含的总的基本事件有:共10个。其中恰有1名观众的年龄为20岁至40岁包含的基本事件有:共6个.
故(“恰有1名观众的年龄为20至40岁”)=;
(2011年高考广东卷第13小题)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间(单位:小时)与当天投篮命中率之间的关系:
时间x
1
2
3
4
5
命中率y
0.4
0.5
0.6
0.6
0.4
小李这5天的平均投篮命中率为 0.5 ;用线形回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 0.53 .
(2011年高考广东卷第17小题) 在某次测验中,有6位同学的平均成绩为75分,用表示编号为的同学所得成绩,且前5位同学的成绩如下:
编号n
1
2
3
4
5
成绩
70
76
72
70
72
(1) 求第6位同学的成绩,及这6位同学成绩的标准差;
(2) 从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
17. 解:(1)
,
(2)从5位同学中随机选取2位同学,共有如下10种不同的取法:
{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5},
选出的2位同学中,恰有1位同学的成绩位于(68,75)的取法共有如下4种取法:
{1,2},{2,3},{2,4},{2,5},
故所求概率为
10.立体几何
2007
2008
2009
2010
2011
17分
17分
18分
19分
24分
(2007年高考广东卷第6小题)
若是互不相同的空间直线,是不重合的平面,则下列命题中为真命题的是( D )
A.若,则 B.若,则
8
图5
6
C.若,则 D.若,则
(2007年高考广东卷第17小题)
已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积;
(2)求该几何体的侧面积.
17解: 由已知可得该几何体是一个底面边长为8和6的矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V-ABCD ;(1)
(2) 该四棱锥有两个侧面VAD、VBC是全等的等腰三角形,且BC边上的高为
, 另两个侧面VAB、VCD也是全等的等腰三角形,
AB边上的高为 因此
(2008年高考广东卷第7小题)
将正三棱柱截去三个角(如图1所示A、B、
C分别是△GHI三边的中点)得到几何体如
图2,则该几何体按图2所示方向的侧视图
(或称左视图)为(A. )
(2008年高考广东卷第18小题)如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP∽△BAD。
(1)求线段PD的长;
(2)若PC = R,求三棱锥P-ABC的体积。
【解析】(1) BD是圆的直径 又 ,
, ;
(2 ) 在中,
又
底面ABCD
三棱锥的体积为 .
(2009年高考广东卷第6小题)给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;w.w.w.k.s.5.u.c.o.m
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是 ( )
A.①和② B.②和③ C.③和④ D.②和④
【答案】D【解析】①错, ②正确, ③错, ④正确.故选D
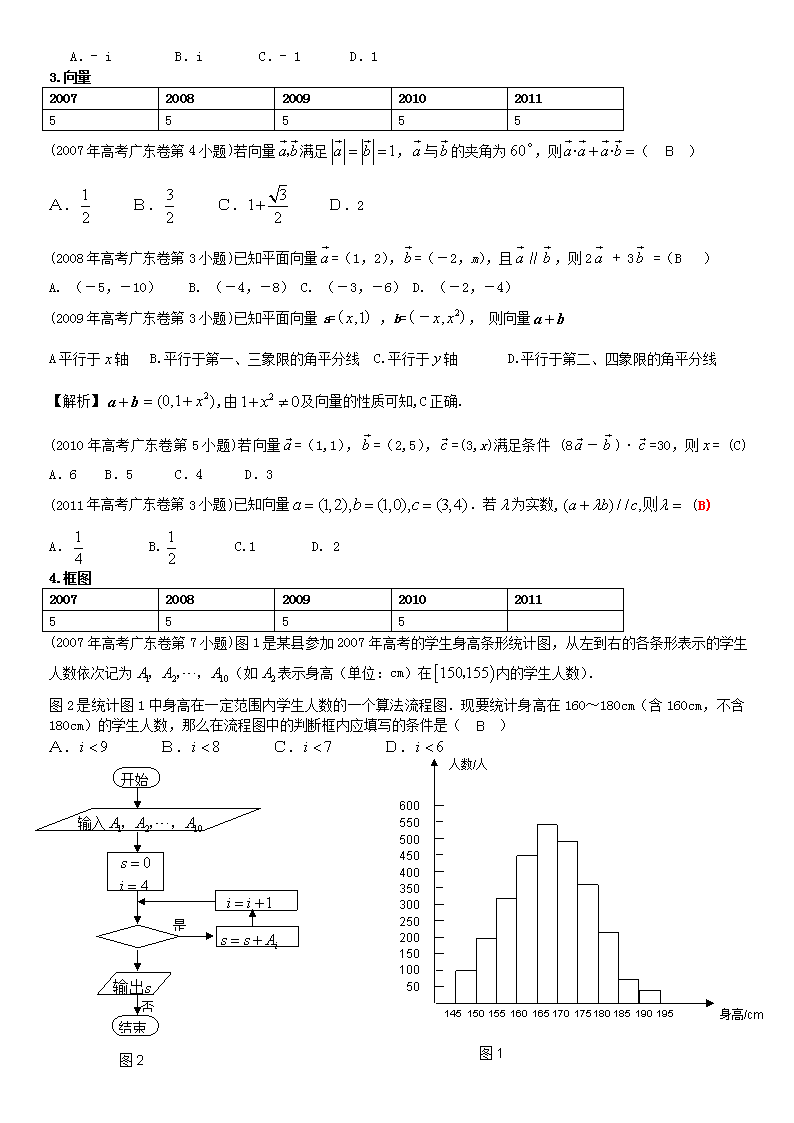
(2009年高考广东卷第17小题)某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积(3)证明:直线BD平面PEG
【解析】(1)侧视图同正视图,如下图所示.
(2)该安全标识墩的体积为:
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知,平面EFGH ,
又 平面PEG 又 平面PEG;w.w.w.k.s.5.u.c.o.m (2010年高考广东卷第9小题)如图1, 为正三角形,,,则多面体的正视图(也称主视图)是wDDddD
(2010年高考广东卷第18小题)如图4,弧是半径为的半圆,为直径,点为弧AC的中点,点和点为线段的三等分点,平面外一点满足平面,=.
(1)证明:;
(2)求点到平面的距离. w_w*w.k_s_5 u.c*o*m
18.法一:(1)证明:∵点B和点C为线段AD的三等分点, ∴点B为圆的圆心
又∵E是弧AC的中点,AC为直径, ∴即
∵平面,平面, ∴又平面,平面且 ∴平面又∵平面, ∴
(2)解:设点B到平面的距离(即三棱锥的高)为.
∵平面, ∴FC是三棱锥F-BDE的高,且三角形FBC为直角三角形
由已知可得,又 ∴
在中,,故,
∴,
又∵平面,故三角形EFB和三角形BDE为直角三角形,
∴,在中,,∴,
∵即,故,
即点B到平面的距离为.
(2011年高考广东卷第7小题)正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱的对角线条数共有D
A.20 B.15 C.12 D. 10
(2011年高考广东卷第9小题)
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体体积为C
A. B.4 C. D. 2
(2011年高考广东卷第18小题) 下图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一般沿切面向右水平平移得到的。分别为
的中点。
(1)证明:四点共面;
(2)设为的中点,延长
证明:(1)中点,
连接BO2
直线BO2是由直线AO1平移得到
共面。
(2)将AO1延长至H使得O1H=O1A,连接
//
由平移性质得=HB
11.平面几何与圆锥曲线
2007
2008
2009
2010
2011
19分
19分
19分
19分
19分
(2007年高考广东卷第11小题)在平面直角坐标系中,已知抛物线关于轴对称,顶点在原点,且过点,则该抛物线的方程是 .
(2007年高考广东卷第19小题)在平面直角坐标系中,已知圆心在第二象限,半径为的圆与直线相切于坐标原点,椭圆与圆的一个交点到椭圆两焦点的距离之和为.
(1)求圆的方程;
(2)试探究圆上是否存在异于原点的点,使到椭圆右焦点的距离等于线段的长.若存在,请求出点的坐标;若不存在,请说明理由.
19解:(1) 设圆C的圆心为 (m, n)(m<0,n>0)依题意可得 解得
所求的圆的方程为
(2) 由已知可得 椭圆的方程为 , 右焦点为 F( 4, 0);
设,依题意
解得或(舍去) 存在点
(2008年高考广东卷第6小题)经过圆的圆心C,且与直线
垂直的直线方程是( C )
A. x + y + 1 = 0 B. x + y - 1 = 0
C. x - y + 1 = 0 D. x - y - 1 = 0
(2008年高考广东卷第20小题)设b>0,椭圆方程为,
抛物线方程为。如图所示,过点F(0,b + 2)
作x轴的平行线,与抛物线在第一象限的交点为G。已知抛
物线在点G的切线经过椭圆的右焦点F1。
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A、B分别是椭圆长轴的左、右端点,试探究在抛物
线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)。
【解析】(1)由得,
当得,G点的坐标为,,,
过点G的切线方程为即,
令得,点的坐标为,由椭圆方程得点的坐标为,
即,即椭圆和抛物线的方程分别为和;
(2)过作轴的垂线与抛物线只有一个交点,以为直角的只有一个,
同理 以为直角的只有一个。
若以为直角,设点坐标为,、两点的坐标分别为和,
。
关于的二次方程有一大于零的解,有两解,即以为直角的有两个,
因此抛物线上存在四个点使得为直角三角形。
(2009年高考广东卷第13小题)以点(2,)为圆心且与直线相切的圆的方程是 .
【答案】
【解析】将直线化为,圆的半径,所以圆的方程为
w.w.w.k.s.5.u.c.o.m
(2009年高考广东卷第19小题)已知椭圆G的中心在坐标原点,长轴在轴上,离心率为,两个焦点分别为和,椭圆G上一点到和的距离之和为12.圆:的圆心为点.
(1)求椭圆G的方程 (2)求的面积 (3)问是否存在圆包围椭圆G?请说明理由.
【解析】(1)设椭圆G的方程为: ()半焦距为c;
则 , 解得 , 所求椭圆G的方程为:. w.w.w.k.s.5.u.c.o.m
(2 )点的坐标为
(3)若,由可知点(6,0)在圆外,
若,由可知点(-6,0)在圆外;
不论K为何值圆都不能包围椭圆G.
(2010年高考广东卷第6小题)若圆心在轴上、半径为的圆位于轴左侧,且与直线相切,则圆的方程是w_w D w. k#s5_u.c o*m
A. B. w_w*w.k_ C. D.
(2010年高考广东卷第7小题)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是w_w B w. k#s5_u.c o*m
A. B. C. D.
(2011年高考广东卷第8小题)设圆 A
A.抛物线 B.双曲线 C.椭圆 D. 圆
(2011年高考广东卷第21小题) 在平面直角坐标系中,直线轴于点,设是上一点,是线段的垂直平分线上的一点,且满足
(1) 当点在上与动时,求点的轨迹的方程;
(2) 已知设是上动点,求的最小值,并给出此时点的坐标;
(3) 过点且不平行于轴的直线与轨迹有且只有两个不同的交点,求直线的斜率的取值范围。
21.(本小题满分14分)
解:(1)如图1,设MQ为线段OP的垂直平分线,交OP于点Q,
因此即 ①
另一种情况,见图2(即点M和A位于直线OP的同侧)。
MQ为线段OP的垂直平分线,
又 因此M在轴上,此时,记M的坐标为
为分析的变化范围,设为上任意点 由 (即)得, 故的轨迹方程为 ②
综合①和②得,点M轨迹E的方程为
(2)由(1)知,轨迹E的方程由下面E1和E2两部分组成(见图3):
;
当时,过T作垂直于的直线,垂足为,交E1于。
再过H作垂直于的直线,交因此,(抛物线的性质)。
(该等号仅当重合(或H与D重合)时取得)。
当时,则
综合可得,|HO|+|HT|的最小值为3,且此时点H的坐标为
(3)由图3知,直线的斜率不可能为零。 设
故的方程得:
因判别式
所以与E中的E1有且仅有两个不同的交点。又由E2和的方程可知,若与E2有交点,
则此交点的坐标为有唯一交点,从而表三个不同的交点。
因此,直线的取值范围是
12.数列
2007
2008
2009
2010
2011
19分
19分
19分
5分
(2007年高考广东卷第13小题) 已知数列的前项和,则其通项 ;若它的第项满足,则 .2n-10 ; 8
(2007年高考广东卷第20小题) 已知函数,是方程的两个根,是的导数.设,.
(1)求的值;
(2)已知对任意的正整数有,记.求数列的前项和.
20解:(1) 由 得
(2)
又
数列是一个首项为 ,公比为2的等比数列;
(2008年高考广东卷第4小题) 记等差数列{an}的前n项和为Sn.若S2=4,S4=20,则该数列的公差d =( B )
A. 2 B. 3 C. 6 D. 7
(2008年高考广东卷第21小题)设数列满足,,(n = 3,4,…)。数列
满足, (n = 2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤…≤1。
(1)求数列和的通项公式;
(2)记(n = 1,2,…),求数列的前n项和。
【解析】(1)由得
又 , 数列是首项为1公比为的等比数列,
,
当n为奇数时
当n为偶数时
由 得 ,由 得 ,…
同理可得当n为偶数时,;当n为奇数时,;因此
当n为奇数时
当n为偶数时
(2)
当n为奇数时,
当n为偶数时
令 ……①
①×得: ……②
①-②得:
当n为奇数时
当n为偶数时
因此
(2009年高考广东卷第5小题)已知等比数列的公比为正数,且·=2,=1,则=
A. B. C. D.2
【答案】B 【解析】设公比为,由已知得,即,因为等比数列的公比为正数,所以,故,选B
(2009年高考广东卷第20小题)已知点(1,)是函数且)的图象上一点,等比数列的前n项和为,数列的首项为c,且前n项和满足-=+(n2).
(1)求数列和的通项公式;
(2)若数列{前n项和为,问>的最小正整数n是多少?
【解析】(1), ,, .又数列成等比数列, ,所以 ;
又公比,所以 ;
又,, ;
数列构成一个首相为1公差为1的等差数列, ,
当, ;();
(2)
;w.w.w.k.s.5.u.c.o.m
由得,满足的最小正整数为112.
(2010年高考广东卷第4小题)已知数列{}为等比数列,是它的前n项和,若,且与的等差中项为,则S5=w_w w. k C #s5_u.c o*m
w_w*w.k_s_5 u.c*o*m A.35 B.33 C.31 D.29
(2011年高考广东卷第11小题)已知是递增等比数列, 2 .
(2011年高考广东卷第20小题) 设数列
(1) 求数列的通项公式;证明:对于一切正整数
20.(本小题满分14分) 解:(1)由
令
当
①当 ②当时,
(2)当
只需
综上所述
13.新题型
2007
2008
2009
2010
2011
5分
5分
5分
图3
(2007年高考广东卷第10小题)
图3是某汽车维修公司的维修点环形分布图.公司在年初分配给四个维修点某种配件各50件.在使用前发现需将四个维修点的这批配件分别调整为,,,件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(件配件从一个维修点调整到相邻维修点的调动件次为)为( C )
A. B. C. D.
(2009年高考广东卷第10小题)
广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表.若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短路线距离是
A. B.21 C.22 D.23
w.w.w.k.s.5 【答案】B【解析】由题意知,所有可能路线有6种:
①,②,③,④,⑤,⑥,
其中, 路线③的距离最短, 最短路线距离等于,
故选B.
(2010年高考广东卷第10小题)
在集合{a,b,c,d}上定义两种运算和如下:w_w w. k#s5_u.c o*m
那么d A
A.a B.b C.c D.d
14.极坐标系与参数方程
2007
2008
2009
2010
2011
5分
5分
5分
5分
5分
(2007年高考广东卷第14小题)在极坐标系中,直线的方程为,则点到直线的距离为 2 .
(2008年高考广东卷第14小题)已知曲线C1、C2的极坐标方程分别为,(,),则曲线C1与C2交点的极坐标为________
(2009年高考广东卷第14小题)若直线(t为参数)与直线垂直,则常数= .
【答案】
【解析】将化为普通方程为,斜率,
当时,直线的斜率,由得;
当时,直线与直线不垂直.综上可知,.
(2010年高考广东卷第14小题)在极坐标系(ρ,)()中,曲线与的交点的极坐标为 . w_w*w.k_s_5 u.c*o*m
(2011年高考广东卷第14小题)已知两曲线参数方程分别为和,它们的交点坐标为 .
图4
15.几何证明选讲
2007
2008
2009
2010
2011
5分
5分
5分
5分
5分
(2007年高考广东卷第15小题)如图4所示,圆的直径,为圆周上一点,,过作圆的切线,过作的垂线,垂足为,则 .
(2008年高考广东卷第15小题)已知PA是圆O的切线,切点为A,PA=2。AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R = ________
(2009年高考广东卷第15小题),点A、B、C是圆O上的点,且AB=4,,则圆O的面积等于 . w.w.w.k.s.5.u.c.o.m
图3 【答案】
【解析】连结AO,OB,因为 ,所以,为等边三角形,故圆O的半径,圆O的面积.
(2010年高考广东卷第15小题)如图3,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF= .
_s_5 u.c*o*m
(2011年高考广东卷第15小题)如图,在梯形中,
则梯形与梯形的面积比为 .