用正多边形铺设地面教案2

用正多边形铺设地面教案2

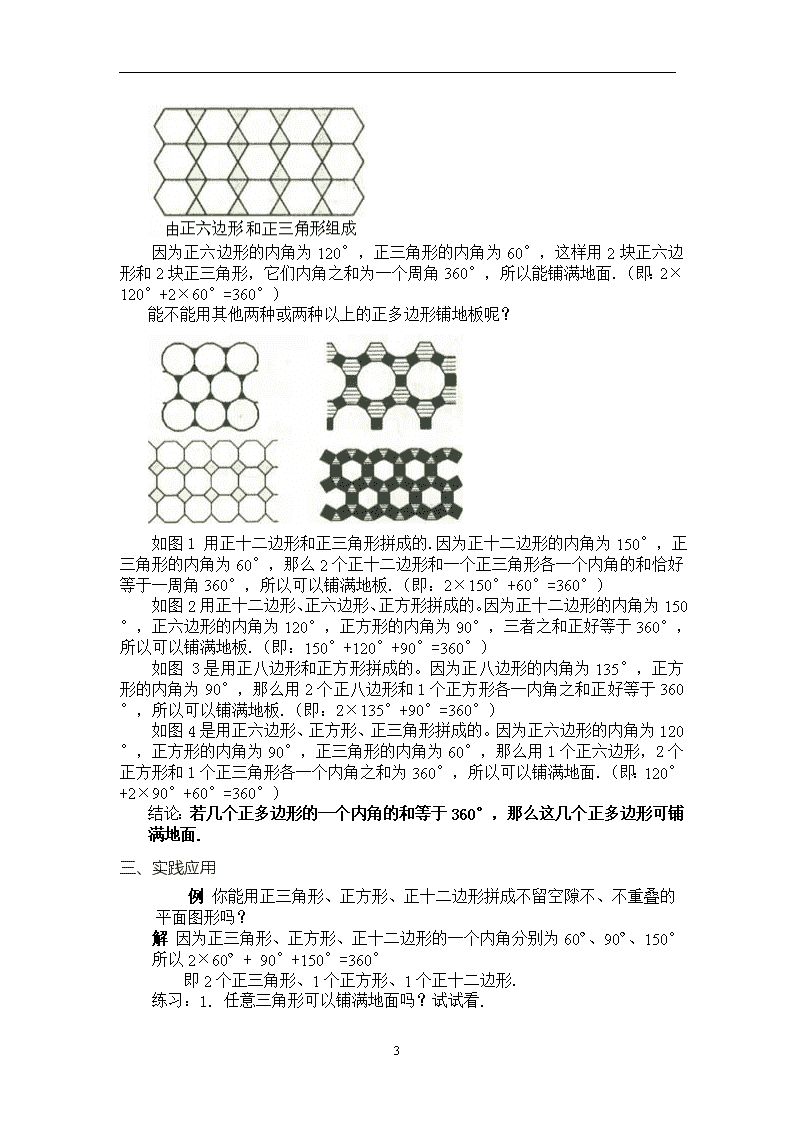
‎ ‎ ‎9.3用正多边形铺设地面（一）‎ 知识技能目标 ‎1．通过用相同的正多边形拼地板活动，巩固多边形的内角和与外角和公式；‎ ‎2．通过“拼地板”和有关计算，使学生从中发现能拼成一个不留空隙，又不重叠的平面图形的关键是几个多边形的内角和相加要等于360º.‎ 过程性目标 ‎1．联系多边形的内角和与外角和公式，经历探索用正多边形拼地板的道理；‎ ‎2．结合实践与应用，充分感受数学知识在实际生活中的应用.‎ 教学过程 一、创设情境 使用给定的某种正多边形，它能否拼成一个平面图形，既不留下一丝空白，又不相互重叠？（请同学们拿出预先准备好的若干张正三角形、正方形、正五边形、正六边形、正八边形）‎ 二、探索归纳 每个内角为多少度时能拼成符合以上条件的平面图形呢？‎ 因为60º×6=360º，用6个正三角形瓷砖就可以铺满地面；‎ ‎ 90º×4=360º，用4个正方形瓷砖就可以铺满地面.‎ 为什么用正五边形瓷砖不能铺满地面呢？正八边形也不行？‎ 因为360º÷108º，360º÷135º得数都不是整数.‎ 当为正整数时；‎ 即为正整数时，用这样的正多边形就可以铺满地面.‎ 结论：当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时，就拼成一个平面图形.‎ 三、实践应用 3‎ ‎ ‎ 例 在正三角形、正方形、正五边形、正六边形、正七边形、正八边形中哪些能铺满地面？为什么？‎ 解 正三角形、正方形、正六边形能铺满地面 因为360º÷60º=6 360º÷90º=4 360º÷120º=3‎ 正五边形、正七边形、正八边形不能铺满地面 因为正五边形、正七边形、正八边形各内角都不能整除360º.‎ 四、交流反思 一种正多边形铺满地面需满足的条件.‎ 五、检测反馈 ‎1．如图，把相邻两行正三角形分开，添一行正方形，得下图，它表明把正三角形和正方形结合在一起也能铺满地面.正三角形、正方形、正六边形两两结合是否能铺满地面呢？把正方形、正六边形结合在一起呢？请你试试看；‎ 2． 请你用正方形铺满地面，设计出2个图案.‎ ‎9.3用正多边形铺设地面（二）‎ 知识技能目标 ‎1．培养良好的情感、态度以及主动参与、合作、交流的意识；‎ ‎2．提高观察、分析、概括、抽象等能力，进一步认识图形在日常生活中的应用.‎ 过程性目标 ‎1．联系一种正多边形拼地板，经历探索用多种正多边形拼地板的过程和原理；‎ ‎2．结合现实世界中的美丽图案，充分感受用多种正多边形拼地板的意义，体会用多种正多边形拼地板与一种正多边形拼地板的相互关系.‎ 教学过程 一、创设情境 用正三角形和正六边形能铺满地面吗？为什么？‎ 二、探索归纳 答 可以，如图 ‎ 因为正六边形的内角为120°，正三角形的内角为60°，这样用2‎ 3‎ ‎ ‎ 块正六边形和2块正三角形，它们内角之和为一个周角360°，所以能铺满地面.（即：2×120°+2×60°=360°）‎ 能不能用其他两种或两种以上的正多边形铺地板呢？‎ 如图1 用正十二边形和正三角形拼成的.因为正十二边形的内角为150°，正三角形的内角为60°，那么2个正十二边形和一个正三角形各一个内角的和恰好等于一周角360°，所以可以铺满地板.（即：2×150°+60°=360°）‎ 如图2用正十二边形、正六边形、正方形拼成的。因为正十二边形的内角为150°，正六边形的内角为120°，正方形的内角为90°，三者之和正好等于360°，所以可以铺满地板.（即：150°+120°+90°=360°）‎ 如图 3是用正八边形和正方形拼成的。因为正八边形的内角为135°，正方形的内角为90°，那么用2个正八边形和1个正方形各一内角之和正好等于360°，所以可以铺满地板.（即：2×135°+90°=360°）‎ 如图4是用正六边形、正方形、正三角形拼成的。因为正六边形的内角为120°，正方形的内角为90°，正三角形的内角为60°，那么用1个正六边形，2个正方形和1个正三角形各一个内角之和为360°，所以可以铺满地面.（即：120°+2×90°+60°=360°）‎ 结论：若几个正多边形的一个内角的和等于360°，那么这几个正多边形可铺满地面.‎ 三、实践应用 例 你能用正三角形、正方形、正十二边形拼成不留空隙不、不重叠的平面图形吗？‎ 解 因为正三角形、正方形、正十二边形的一个内角分别为60º、90º、150°‎ 所以2×60º + 90°+150°=360°‎ 即2个正三角形、1个正方形、1个正十二边形.‎ ‎ 练习：1. 任意三角形可以铺满地面吗？试试看.‎ ‎2．用正方形和正八边形组合能铺满地面吗？为什么？‎ 四、交流反思 用多种正多边形拼地板：用多种正多边形拼地板的原理：几个正多边形的一个内角和等于360°.‎ 五、检测反馈 ‎1．试画出用正三角形和正六边形铺满地面，但与上面的图形不同的图形；‎ ‎2．在一个城市的地图上，4个区的轮廓都是三角形形状，如果每个区与其他3个区都有公共边界，各区彼此的位置怎样？请画出示意图；‎ ‎3．以“瓷砖中的数学”为题写一篇小论文.‎ 3‎