- 2021-04-21 发布 |
- 37.5 KB |
- 17页
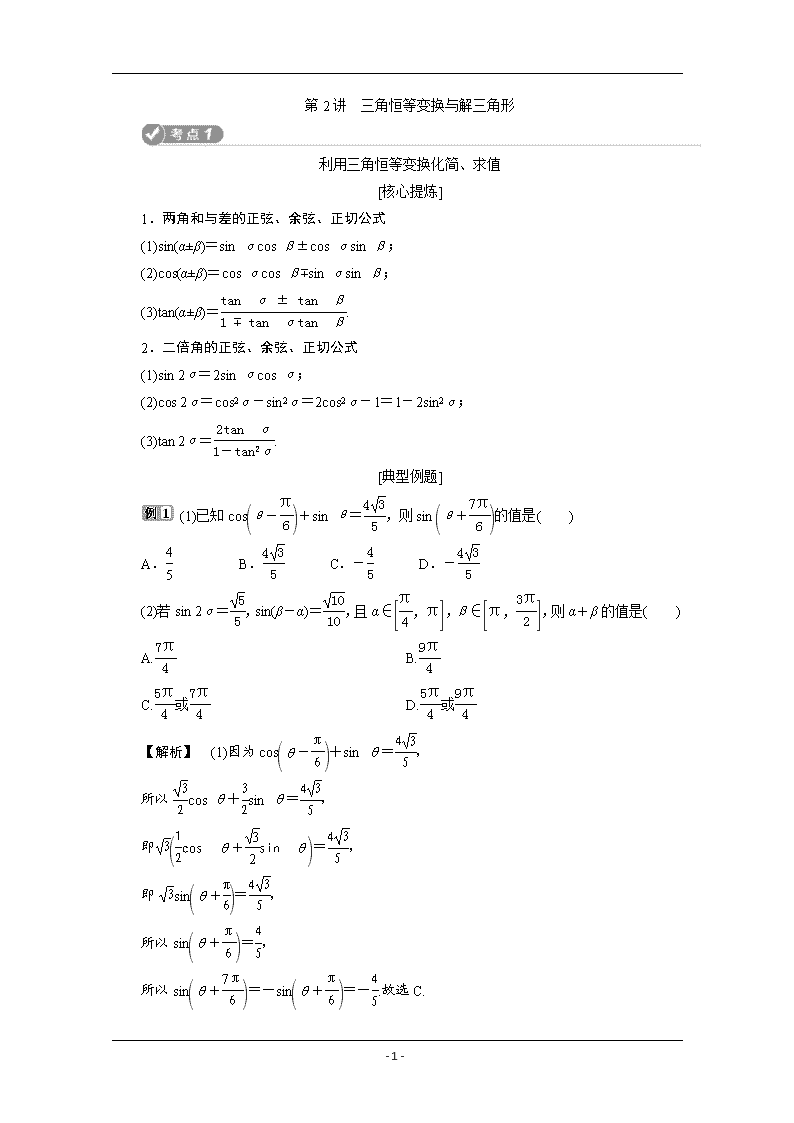

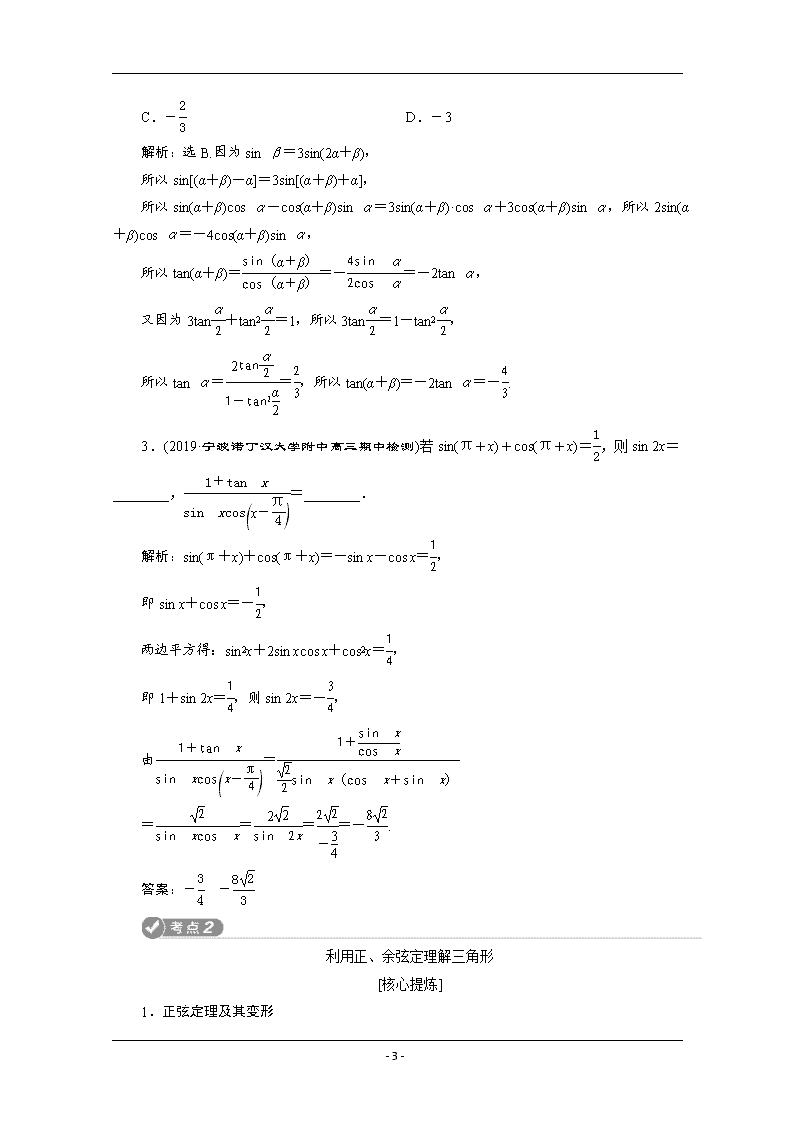
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020浙江新高考数学二轮复习教师用书:专题二 2 第2讲 三角恒等变换与解三角形
- 1 - 第 2讲 三角恒等变换与解三角形 利用三角恒等变换化简、求值 [核心提炼] 1.两角和与差的正弦、余弦、正切公式 (1)sin(α±β)=sin αcos β±cos αsin β; (2)cos(α±β)=cos αcos β∓sin αsin β; (3)tan(α±β)=tan α±tan β 1∓tan αtan β . 2.二倍角的正弦、余弦、正切公式 (1)sin 2α=2sin αcos α; (2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α; (3)tan 2α= 2tan α 1-tan2α . [典型例题] (1)已知 cos θ- π 6 +sin θ= 4 3 5 ,则 sin θ+ 7π 6 的值是( ) A.4 5 B.4 3 5 C.- 4 5 D.- 4 3 5 (2)若 sin 2α= 5 5 ,sin(β-α)= 10 10 ,且α∈ π 4 ,π ,β∈ π, 3π 2 ,则α+β的值是( ) A.7π 4 B.9π 4 C.5π 4 或 7π 4 D.5π 4 或 9π 4 【解析】 (1)因为 cos θ- π 6 +sin θ= 4 3 5 , 所以 3 2 cos θ+ 3 2 sin θ= 4 3 5 , 即 3 1 2 cos θ+ 3 2 sin θ = 4 3 5 , 即 3sin θ+ π 6 = 4 3 5 , 所以 sin θ+ π 6 = 4 5 , - 2 - 所以 sin θ+ 7π 6 =-sin θ+ π 6 =- 4 5 .故选 C. (2)因为α∈ π 4 ,π ,所以 2α∈ π 2 ,2π ,又 sin 2α= 5 5 ,故 2α∈ π 2 ,π ,α∈ π 4 , π 2 , 所以 cos 2α=- 2 5 5 .又β∈ π, 3π 2 ,故β-α∈ π 2 , 5π 4 ,于是 cos(β-α)=- 3 10 10 ,所以 cos(α+β)=cos[2α+(β-α)]=cos 2αcos(β-α)-sin 2αsin(β-α)=- 2 5 5 × - 3 10 10 - 5 5 × 10 10 = 2 2 ,且α+β∈ 5π 4 ,2π ,故α+β=7π 4 . 【答案】 (1)C (2)A 三角函数恒等变换“四大策略” (1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等; (2)项的分拆与角的配凑:如 sin2α+2cos2α=(sin2α+cos2α)+cos2α,α=(α-β)+β等; (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次; (4)弦、切互化:一般是切化弦. [对点训练] 1.(2019·杭州市高三模拟)函数 f(x)=3sin x 2 cosx 2 +4cos2x 2 (x∈R)的最大值等于( ) A.5 B.9 2 C.5 2 D.2 解析:选 B.因为 f(x)=3sin x 2 cos x 2 +4cos2x 2 = 3 2 sin x+2cos x+2=5 2 3 5 sin x+4 5 cos x +2 = 5 2 sin(x+φ)+2, 其中 sin φ=4 5 ,cos φ=3 5 , 所以函数 f(x)的最大值为 9 2 . 2.(2019·浙江五校联考)已知 3tan α 2 +tan2α 2 =1,sin β=3sin(2α+β),则 tan(α+β)= ( ) - 3 - A.4 3 B.- 4 3 C.- 2 3 D.-3 解析:选 B.因为 sin β=3sin(2α+β), 所以 sin[(α+β)-α]=3sin[(α+β)+α], 所以 sin(α+β)cos α-cos(α+β)sin α=3sin(α+β)·cos α+3cos(α+β)sin α,所以 2sin(α +β)cos α=-4cos(α+β)sin α, 所以 tan(α+β)=sin(α+β) cos(α+β) =- 4sin α 2cos α =-2tan α, 又因为 3tanα 2 +tan2α 2 =1,所以 3tanα 2 =1-tan2α 2 , 所以 tan α= 2tanα 2 1-tan2α 2 = 2 3 ,所以 tan(α+β)=-2tan α=- 4 3 . 3.(2019·宁波诺丁汉大学附中高三期中检测)若 sin(π+x)+cos(π+x)=1 2 ,则 sin 2x= ________, 1+tan x sin xcos x-π 4 =________. 解析:sin(π+x)+cos(π+x)=-sin x-cos x=1 2 , 即 sin x+cos x=- 1 2 , 两边平方得:sin2x+2sin xcos x+cos2x=1 4 , 即 1+sin 2x=1 4 ,则 sin 2x=- 3 4 , 由 1+tan x sin xcos x-π 4 = 1+sin x cos x 2 2 sin x(cos x+sin x) = 2 sin xcos x = 2 2 sin 2x = 2 2 - 3 4 =- 8 2 3 . 答案:- 3 4 - 8 2 3 利用正、余弦定理解三角形 [核心提炼] - 4 - 1.正弦定理及其变形 在△ABC中, a sin A = b sin B = c sin C =2R(R为△ABC的外接圆半径).变形:a=2Rsin A,sin A= a 2R ,a∶b∶c=sin A∶sin B∶sin C等. 2.余弦定理及其变形 在△ABC中,a2=b2+c2-2bccos A; 变形:b2+c2-a2=2bccos A,cos A=b2+c2-a2 2bc . 3.三角形面积公式 S△ABC= 1 2 absin C=1 2 bcsin A=1 2 acsin B. [典型例题] (1)(2018·高考浙江卷)在△ABC中,角 A,B,C所对的边分别为 a,b,c.若 a= 7, b=2,A=60°,则 sin B=________,c=________. (2)在△ABC中,内角 A,B,C所对的边分别为 a,b,c.已知 b+c=2acos B. ①证明:A=2B; ②若 cos B=2 3 ,求 cos C的值. 【解】 (1)因为 a= 7,b=2,A=60°,所以由正弦定理得 sin B=bsin A a = 2× 3 2 7 = 21 7 . 由余弦定理 a2=b2+c2-2bccos A可得 c2-2c-3=0,所以 c=3.故填: 21 7 3. (2)①证明:由正弦定理得 sin B+sin C =2sin Acos B, 故 2sin Acos B=sin B+sin(A+B)=sin B+ sin Acos B+cos Asin B,于是 sin B=sin(A-B). 又 A,B∈(0,π),故 0<A-B<π, 所以 B=π-(A-B)或 B=A-B, 因此 A=π(舍去)或 A=2B, 所以 A=2B. ②由 cos B=2 3 得 sin B= 5 3 , cos 2B=2cos2B-1=- 1 9 , 故 cos A=- 1 9 ,sin A=4 5 9 , - 5 - cos C=-cos(A+B)=-cos Acos B+sin Asin B=22 27 . 正、余弦定理的适用条件 (1)“已知两角和一边”或“已知两边和其中一边的对角”应利用正弦定理. (2)“已知两边和这两边的夹角”或“已知三角形的三边”应利用余弦定理. [对点训练] 1.(2019·高考浙江卷)在△ABC中,∠ABC=90°,AB=4,BC=3,点 D在线段 AC上.若 ∠BDC=45°,则 BD=________,cos∠ABD=________. 解析:在 Rt△ABC 中,易得 AC=5,sin C=AB AC = 4 5 .在△BCD 中,由正弦定理得 BD= BC sin∠BDC ×sin∠BCD= 3 2 2 × 4 5 = 12 2 5 ,sin∠DBC=sin[π-(∠BCD+∠BDC)]=sin(∠BCD+ ∠BDC)=sin ∠BCDcos∠BDC+cos∠BCDsin∠BDC=4 5 × 2 2 + 3 5 × 2 2 = 7 2 10 .又∠ABD+ ∠DBC=π 2 ,所以 cos∠ABD=sin∠DBC=7 2 10 . 答案: 12 2 5 7 2 10 2.(2019·义乌高三月考)在△ABC中,内角 A,B,C对应的三边长分别为 a,b,c,且满 足 c bcos A-a 2 =b2-a2. (1)求角 B的大小; (2)若 BD为 AC边上的中线,cos A=1 7 ,BD= 129 2 , 求△ABC的面积. 解:(1)因为 c bcos A- a 2 =b2-a2, 即 2bccos A-ac=2(b2-a2), 所以 b2+c2-a2-ac=2(b2-a2), 所以 a2+c2-b2=ac,cos B=1 2 ,B=π 3 . (2)法一:在三角形 ABD中, 由余弦定理得 129 2 2 =c2+ b 2 2 -2c·b 2 cos A, 所以 129 4 =c2+b2 4 - 1 7 bc,① - 6 - 在三角形 ABC中,由已知得 sin A=4 3 7 , 所以 sin C=sin(A+B)=sin Acos B+cos Asin B=5 3 14 , 由正弦定理得 c=5 7 b.② 由①,②解得 b=7, c=5. 所以 S△ABC= 1 2 bcsin A=10 3. 法二:延长 BD到 E,DE=BD, 连接 AE,在△ABE中, ∠BAE=2π 3 , BE2=AB2+AE2-2·AB·AE·cos ∠BAE, 因为 AE=BC, 129=c2+a2+a·c,① 由已知得,sin ∠BAC=4 3 7 , 所以 sin C=sin(A+B)=5 3 14 , c a = sin ∠ACB sin ∠BAC = 5 8 .② 由①②解得 c=5,a=8, S△ABC= 1 2 c·a·sin ∠ABC=10 3. 解三角形中的最值(范围)问题 [典型例题] (1)在△ABC中,角 A,B,C所对的边分别为 a,b,c.已知 2ccos B=2a-b. ①求角 C的大小; ②若|CA → - 1 2 CB→|=2,求△ABC面积的最大值. (2)(2019·杭州市高考数学二模)在△ABC中,内角 A,B,C所对的边分别为 a,b,c,若 msin A=sin B+sin C(m∈R). ①当 m=3时,求 cos A的最小值; ②当 A=π 3 时,求 m的取值范围. - 7 - 【解】 (1)①因为 2ccos B=2a-b, 所以 2sin Ccos B=2sin A-sin B=2sin(B+C)-sin B, 化简得 sin B=2sin Bcos C, 因为 sin B≠0,所以 cos C=1 2 . 因为 0<C<π,所以 C=π 3 . ②取 BC的中点 D,则|CA → - 1 2 CB→|=|DA→ |=2. 在△ADC中,AD2=AC2+CD2-2AC·CDcos C, 即有 4=b2+ a 2 2 - ab 2 ≥2 a2b2 4 - ab 2 = ab 2 , 所以 ab≤8,当且仅当 a=4,b=2时取等号. 所以 S△ABC= 1 2 absin C= 3 4 ab≤2 3, 所以△ABC面积的最大值为 2 3. (2)①因为在△ABC中 msin A=sin B+sin C, 当 m=3时, 3sin A=sin B+sin C, 由正弦定理可得 3a=b+c, 再由余弦定理可得 cos A=b2+c2-a2 2bc = b2+c2-1 9 (b+c)2 2bc = 8 9 (b2+c2)- 2 9 bc 2bc ≥ 8 9 ·2bc-2 9 bc 2bc = 7 9 , 当且仅当 b=c时取等号, 故 cos A的最小值为 7 9 . ②当 A=π 3 时,可得 3 2 m=sin B+sin C, 故 m=2 3 3 sin B+2 3 3 sin C = 2 3 3 sin B+2 3 3 sin 2π 3 -B = 2 3 3 sin B+2 3 3 3 2 cos B+1 2 sin B - 8 - = 2 3 3 sin B+cos B+ 3 3 sin B = 3sin B+cos B=2sin B+π 6 , 因为 B∈ 0,2π 3 , 所以 B+π 6 ∈ π 6 , 5 6 π , 所以 sin B+π 6 ∈ 1 2 ,1 , 所以 2sin B+π 6 ∈(1,2], 所以 m的取值范围为(1,2]. (1)求最值的一般思路 由余弦定理中含两边和的平方(如 a2+b2-2abcos C=c2)且 a2+b2≥2ab,因此在解三角形 中,若涉及已知条件中含边长之间的关系,且与面积有关的最值问题,一般利用 S=1 2 absin C 型面积公式及基本不等式求解,有时也用到三角函数的有界性. (2)求三角形中范围问题的常见类型 ①求三角形某边的取值范围. ②求三角形一个内角的取值范围,或者一个内角的正弦、余弦的取值范围. ③求与已知有关的参数的范围或最值. [对点训练] 1.在△ABC中,AC→ ·AB→=|AC→-AB→ |=3,则△ABC面积的最大值为( ) A. 21 B.3 21 4 C. 21 2 D.3 21 解析:选 B.设角 A,B,C所对的边分别为 a,b,c, 因为AC→·AB→=|AC→-AB→ |=3, 所以 bccos A=a=3. 又 cos A=b2+c2-a2 2bc ≥1- 9 2bc =1-3cos A 2 , 所以 cos A≥2 5 , - 9 - 所以 0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档