【40套试卷合集】甘肃省定西市名校2019-2020学年数学九上期末模拟试卷含答案

【40套试卷合集】甘肃省定西市名校2019-2020学年数学九上期末模拟试卷含答案

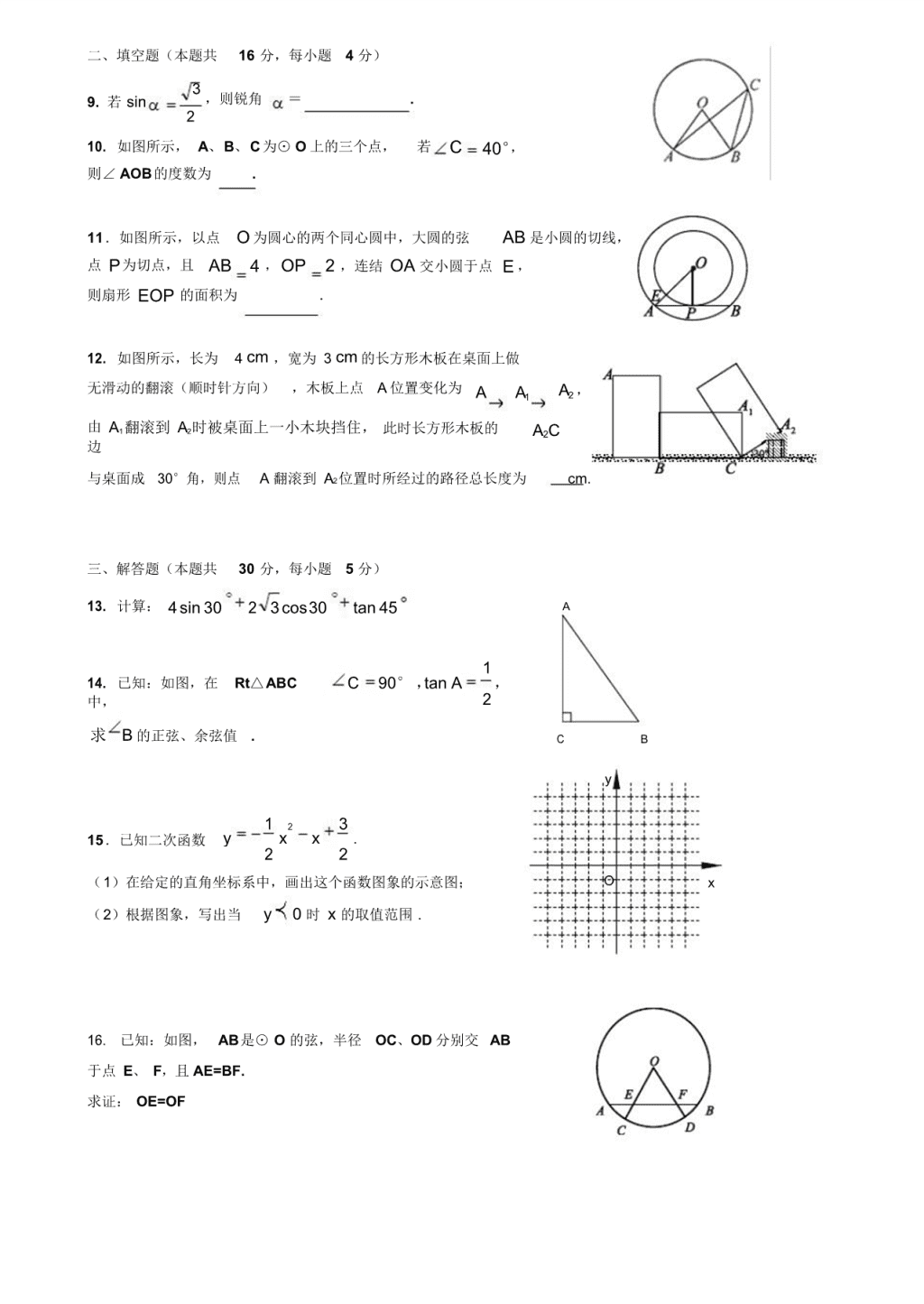
2019-2020 学年九上数学期末模拟试卷含答案 一、选择题（本题共 32 分，每小题 4 分） 下面各题均有四 个选项，其中只有一个 ．．是符合题意的． 1 ）的双曲线的解析式是（ ） 1. 经过点 P（ 2 ， 4 A. y 2 x x B. y 1 2x 2 C. y D. y 2 x 2. 如图所示，在△ ABC 中， DE//BC 分别交 AB、AC 于点 D、 E， AE=1，EC=2，那么 AD 与 AB 的比为 A. 1：2 B. 1：3 C. 1：4 D. 1：9 3. 一个袋子中装有 6 个红球 3 个白球，这些球除颜色外，形状、大小、质地等完全相同．在看不到球的 条件下，随机地从这个袋子中摸出一个球，摸到红球的概率为 1 1 1 2 A． B． C． D． 2 9 3 3 4. 抛物线 y 2(x 2) 2 5 的顶点坐标是 A. （ -5，-2） B. 2， 5 C. 2， 5 D. （-5，2） 5. △ ABC 在正方形格纸中的位置如图所示，则 sin 的值是 3 3 A. B. 5 4 4 4 C. D. 3 5 6. 要得到函数 y 2x2 1的图象，应将函数 y 2x 2 的图象 A.沿 x 轴向左平移 1 个单位 B. 沿 x 轴向右平移 1 个单位 C. 沿 y 轴向上平移 1 个单位 D. 沿 y 轴向下平移 1 个单位 7. 在平面直角坐标系中，如果⊙ O 是以原点为圆心，以 10 为半径的圆，那么点 A（-6，8） A. 在⊙ O 内 B. 在⊙ O 外 C. 在⊙ O 上 D. 不能确定 8．已知函数 y (x a)( x b) （其中 a b ）的图象如图所示，则函数 y ax b 的图象可能正确的是 二、填空题（本题共 16 分，每小题 4 分） 9. 若 sin 3 ，则锐角 ＝ . 2 10. 如图所示， A、B、C为⊙ O 上的三个点， 若 C 则∠ AOB的度数为 . 40°， 11．如图所示，以点 O 为圆心的两个同心圆中，大圆的弦 AB 是小圆的切线， 点 P为切点，且 AB 4 ，OP 2 ，连结 OA 交小圆于点 E ， 则扇形 EOP 的面积为 ． 12. 如图所示，长为 4 cm ，宽为 3 cm 的长方形木板在桌面上做 无滑动的翻滚（顺时针方向） ，木板上点 A 位置变化为 A A1 A2 ， 由 A1 翻滚到 A2时被桌面上一小木块挡住， 此时长方形木板的 边 A2C 与桌面成 30°角，则点 A 翻滚到 A2 位置时所经过的路径总长度为 cm. 三、解答题（本题共 30 分，每小题 5 分） 13. 计算： 4sin 30 2 3cos30 tan 45 A 14. 已知：如图，在 Rt△ABC 中， 1 C 90° ，tan A ， 2 求 B 的正弦、余弦值 . C B y 1 2 3 15．已知二次函数 y x x . 2 2 （1）在给定的直角坐标系中，画出这个函数图象的示意图； O x （2）根据图象，写出当 y 0 时 x 的取值范围 . 16. 已知：如图， AB是⊙ O 的弦，半径 OC、OD 分别交 AB 于点 E、 F，且 AE=BF. 求证： OE=OF 17.已知：如图，将正方形 ABCD 纸片折叠，使顶点 A 落在边 CD 上的 点 P 处( 点 P 与 C、D 不重合 ) ，点 B 落在点 Q 处，折痕为 EF，PQ 与 BC 交于点 G． 求证：△ PCG∽△ EDP. 18．在一个不透明的口袋中装有白、黄两种颜色的乒乓球（除颜色外其余都相同） ，其中黄球有 1 个，白球有 2 个. 第一次摸出一个球，做好记录后放回袋中，第二次再摸出一个球，请用列表或画树状图的方法求两 次都摸到黄球的概率 . 四、解答题（本题共 20 分，每小题 5 分） 1 1 19．已知如图，在平面直角坐标系 xoy中，直线 y x 与 2 2 k x 轴交于点 A，与双曲线 y 在第一象限内交于点 B， x BC 垂直 x 轴于点 C，OC=2AO．求双曲线 k y 的解析式． x 20．已知：如图，一架直升飞机在距地面 450 米上空的 P 点， 测得 A 地的俯角为 30 ， B 地的俯角为 60 （点 P 和 AB所在 的直线在同一垂直平面上） ，求 A、B 两地间的距离． 21.作图题（要求用直尺和圆规作图，不写出作法， 只保留作图痕迹，不要求写出证明过程） . 已 知：圆 . 求作：一条线段，使它把已知圆分成面积相等的两部分． 22. 已知如图，△ ABC 内接于⊙ O，且 AB=AC=13， BC=24， PA∥ BC，割线 PBD 过圆心，交⊙ O 于另一个点 D，联结 CD． ⑴求证： PA 是⊙ O 的切线； ⑵求⊙ O 的半径及 CD 的长． 五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分） 23. 已知：在 △ ABC 中， AB AC ，点 D 为 BC 边的中点，点 F 在 AB 上，连结 DF 并延长到点 E ,使 BAE BDF ，点 M 在线段 DF 上，且 ABE DBM ． （ 1）如图 1，当 ABC 45°时， 求证： AE 2 MD； （ 2）如图 2，当 ABC 60°时， 则线段 AE、MD 之间的数量关系为 ； （3）在（ 2）的条件下，延长 BM 到 P ，使 MP BM ， 连接 CP ，若 AB 7，AE 2 7 ，求 tan EAB 的值． 24.已知 a、b 均为整数，直线 y ax b 与三条抛物线 y 2 x 3, y 2 x 6x 7 和 y 2 x 4x 5 交 点的个数分别是 2,1,0，若 bx 2 ay 2 6x，求 x 2 y 2 的最大值 . 1 2 3 25.已知二次函数 y x x . 4 2 （1）求它的对称轴与 x 轴交点 D 的坐标； （2）将该抛物线沿它的对称轴向上平移，如图所示，设平移后的抛物线的顶点为 M ，与 x 轴、 y 轴的交 点分别为 A、B、C 三点，连结 AC、BC,若∠ ACB=90°. ①求此时抛物线的解析式； ②以 AB 为直径作圆，试判断直线 CM 与此圆的位置关系，并说明理由 . 初三数学 参考答 案及评分标准 阅卷须知： 1．为便于阅卷，本试卷答案中有关解答题的推导步骤写得较为详细，阅卷时，只要考生将主要过程 正确写出即可。 2．若考生的解法与给出的解法不同，正确者可参照评分参考相应给分。 3．评分参考中所注分数，表示考生正确做到此步应得的累加分数。 一、选择题（本题共 32 分，每小题 4 分） 题 号 1 2 3 4 5 6 7 8 答 案 B B D C A D C D 二、填空题（本题共 16 分，每小题 4 分） 题 号 9 10 11 12 答 案 60° 80° 1 π 7 2 2 三、解答题（本题共 30 分，每小题 5 分） 13. 解：原式 1 3 4 2 3 1 3 分 2 2 6 5 分 14.解：如图所示，在 Rt ABC 中 C 90 ， 1 tan A 2 设 BC x,AC 2x..................................................1 分 AB 5 x..............................................................2分 sin B AC AB 2x 2 5x 5 5........................................3 分 cosB x 5 .......................................................5 分 5x 5 15.（ 1）示意图正确 3 分 （ 2）当 y ＜ 0 时， x 的取值范围是 x＜ -3 或 x＞1； 5 分 16. 证明：过点 O 作 OM ⊥ AB 于 M 1 分 ∴AM=BM 3 分 ∵AE=BF ， ∴EM=FM 4 分 ∴ OE= 5 分 17.证明： ABCD 是正方形， A C D PED DPE 由折叠知 , 90 .......................................................2分 90 , EPQ A 90 DPE CPG 90 . PED CPG.......................................................... ......4 分 GCP∽ EDP .................................................................5 分 18.解： 依题意，列表为： 黄 白 白 黄 （黄，黄） （黄，白） （黄，白） 白 （白，黄） （白，白） （白，白） 3 分 白 （白，黄） （白，白） （白，白） 由上表可知，共有 9 种结果，其中两次都摸到黄球的结果只有 1 种， 所以两次都摸到黄球的概率为 四、解答题（本题共 20 分，每小题 5 分） 1 . 5 分 9 19．解：在 1 1y x 中，令 y=0，得 2 2 1 1 x 0 ． 2 2 解得 x 1． ∴直线 y 1 1 x 与 x 轴的交点 A 的坐标为：（-1，0） 2 2 ∴AO=1 ． ∵OC=2AO ， ∴OC=2 ． 2 分 ∵BC ⊥x 轴于点 C ， ∴点 B 的横坐标为 2． ∵点 B 在直线 1 1 y x 上， 2 2 B 1 1 3∴ y 2 ． 2 2 2 ∴点 B 的坐标为 k 3 (2 ，）． 4 分 2 3∵双曲线 y 过点 B (2 ，）， x 2 3 k∴ ． 2 2 解得 k 3． ∴双曲线的解析式为 y 3 ． 5 分 x 20.解：过点 P 做 PC AB, 交AB 延长线于点 C. 根据题意得， PAB PBC APB 30 ， 60 60 30 30 ， APB PAB, AB PB......................................................................................2 分 在Rt BCP 中， C 90 ， Q 30 P PBC 60 ， 60 450 PC PB 900 3 450， 450 sin 60 A B C 300 3........................................................................................4 分 AB PB 300 3 答： A、B 两地间的距 离 300 3 米 .......................................5分 21. AB 为所求直线 . 5 分 P A C 22． G O D 2 2 22 2 证明：（1）联结 OA 、OC ，设 OA 交 BC 于 G． ∵AB=AC ， ∴ AB = AC ∴ AOB= AOC. ∵OB=OC， ∴OA ⊥BC ． ∴ OGB =90° ∵PA∥BC， ∴ OAP = OGB =90° ∴OA ⊥PA． ∴PA 是⊙ O 的切线． 2 分 （ 2）∵ AB=AC ，OA ⊥ BC，BC=24 ∴ BG= 1 BC=12 ． 2 ∵ AB=13， ∴AG= 13 12 5． 3 分 设⊙ O的半径为 R，则 OG=R － 5． 在 Rt△ OBG 中，∵ OB 2 BG OG ， R 12 （R - 5）2 ． 解得， R=16.9 4 分 ∴OG=11.9 ． ∵BD 是⊙ O 的直径， ∴O 是 BD 中点， ∴OG 是△ BCD 的中位线． ∴DC=2OG=23.8 ． 5 分 23.（ 1）证明：如图 1 连结 AD AB AC , BD CD AD BC. 又 ABC 45° BD AB cos ABC 即AB 2 BD............................................................1 分 BAE BDM ABE DBM △ABE∽△ DBM ...............................................2 分 AE AB 2 DM DB AE 2MD ...........................................................3 分 2 2 （ 2）AE 2MD 4 分 （ 3）解：如图 2 连结 AD、EP , ABE ∽ AEB DBM BMD BE AB 2 BM DB ∴ EB 2BM 又 BM MP , EB BP . ∵ ABE DBM EBP ABC 60 △BEP 为等边三角形 ..5 分 EM BMD BP, 90 AEB BMD 90 在 Rt△AEB 中, AE 2 7 , AB 7 , BE AB AE 21....................................6 分 tan EAB 3 ...................................................7 分 2 3 tan∠EAB 的值为 2 2 2 2 2 2 2 2 2 2 24.解：由题意，得 2 x 3 ax b ① x 6x 7 2 x 4x 5 ax b ② ax b ③ 方程 ①有两个不等实根，方程 2 ②有两个相等实根，方程 ③无实数根 . 1 a 4b 2 12 0 ④ 2 a 12a 2 3 a 8a 4b 8 0 ⑤ 4b 4 0 ⑥ 2 ...................................1 分 由⑤得 4b ⑦ 代入 ④、⑥得 (a 12a 8) ⑦ . 2 2 a 12 (a 2 12a 2 8) 0 a 8a 4 (a 12a 8) 0 解此不等式组，得 5 a 3......................................................................................2 分 3 因为 a 是整数，所以有 a 2. 于是 4b 12,得b 3 a 2,b 3x 2 y 3............................................................................................3 分 6x, 2 6x 3x y 2 ...........................................................................................4 分 2 6x 3x y 0, 2 2 6x 3x 0 x(2 x) 0 x 0, x 0,或 2 x 0 2 x 0 0 x 2..............................................................................................5 分 2 2 设 Z x y 2 6x 3xx 2 1 x 3x 2 1 (x 3) 9...................................................................................6 分 2 2 当x 3 时,函数 Z 随 x 的增大而增大 , 当x 即当 x 2 时， Z 最大值 2 时， x y 4 有最大值 4........................................................7 分 25．解（ 1）由 y 1 x 2 3 x4 2 得 x b 3 2a ∴Ｄ（ 3， 0） 1 分 （2）∵ y 1 2 3x x 1 2 3 4 2 ∴顶点坐标 3,9 4 y x x 4 2 2 2