- 2021-04-21 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年山东省济南市章丘区七年级(上)期末数学试卷
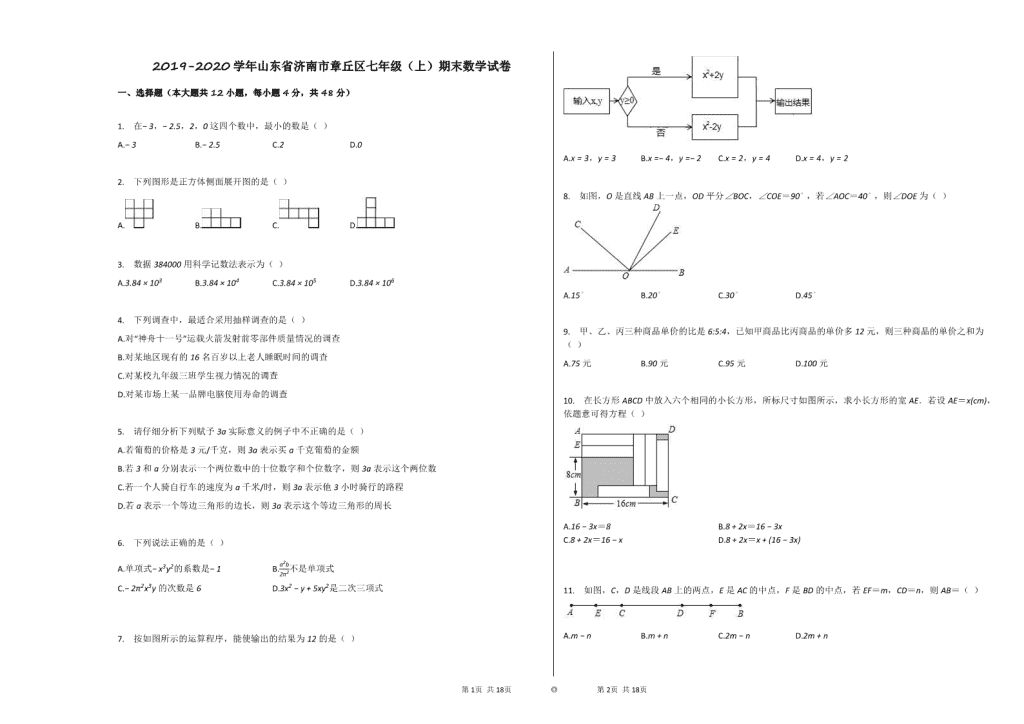
2019-2020学年山东省济南市章丘区七年级(上)期末数学试卷 一、选择题(本大题共12小题,每小题4分,共48分) 1. 在−3,−2.5,2,0这四个数中,最小的数是( ) A.−3 B.−2.5 C.2 D.0 2. 下列图形是正方体侧面展开图的是( ) A. B. C. D. 3. 数据384000用科学记数法表示为( ) A.3.84×103 B.3.84×104 C.3.84×105 D.3.84×106 4. 下列调查中,最适合采用抽样调查的是( ) A.对“神舟十一号”运载火箭发射前零部件质量情况的调查 B.对某地区现有的16名百岁以上老人睡眠时间的调查 C.对某校九年级三班学生视力情况的调查 D.对某市场上某一品牌电脑使用寿命的调查 5. 请仔细分析下列赋予3a实际意义的例子中不正确的是( ) A.若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额 B.若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数 C.若一个人骑自行车的速度为a千米/时,则3a表示他3小时骑行的路程 D.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长 6. 下列说法正确的是( ) A.单项式−x3y2的系数是−1 B.a2b2π2不是单项式 C.−2π2x3y的次数是6 D.3x2−y+5xy2是二次三项式 7. 按如图所示的运算程序,能使输出的结果为12的是( ) A.x=3,y=3 B.x=−4,y=−2 C.x=2,y=4 D.x=4,y=2 8. 如图,O是直线AB上一点,OD平分∠BOC,∠COE=90∘,若∠AOC=40∘,则∠DOE为( ) A.15∘ B.20∘ C.30∘ D.45∘ 9. 甲、乙、丙三种商品单价的比是6:5:4,已知甲商品比丙商品的单价多12元,则三种商品的单价之和为( ) A.75元 B.90元 C.95元 D.100元 10. 在长方形ABCD中放入六个相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),依题意可得方程( ) A.16−3x=8 B.8+2x=16−3x C.8+2x=16−x D.8+2x=x+(16−3x) 11. 如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若EF=m,CD=n,则AB=( ) A.m−n B.m+n C.2m−n D.2m+n 第17页 共18页 ◎ 第18页 共18页 12. 为了求1+2+22+23+...+22019的值,可令S=1+2+22+23+...+22019,则2S=2+22+23+...+22019+22020,因此2S−S=22020−1,所以1+2+22+23+...+22019=22020−1.请仿照以上推理计算:1+4+42+43+...+42019的值是( ) A.42100−1 B.42020−1 C.42019−13 D.42020−13 二.填空题(本大题共6小题,每小题4分,共24分) 若代数式2a2+3b的值是6,则代数式4a2+6b+8的值是________. 已知x=5是方程ax−8=20+a的解,则a=________. 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有________人. 若2xm−3y5与−3x2yn+2的和是单项式,则m+n=________. 线段AB=12cm,点C在线段AB上,且AC=13BC,M为BC的中点,则AM的长为 7.5 cm. 如图,a、b、c、d、e、f均为有理数,图中各行、各列及两条对角线上三个数的和都相等,则a+b+c+d+e+f的值是________. 4 −1 a b 3 c d e f 三、解答题(本大题共9小题,共78分) 计算与化简: (1)−32−(−32)2×29−6÷(−23) (2)(−2ab+3a)−2(2a−b)+2ab 如图是由几个小立方体所搭几何体的俯视图,小正方体的数字表示在该位置的小立方体的个数,请你画出这个几何体从正面和左面看到的图形.(在所提供的方格内涂上相应的阴影即可) 先化简,再求值b2−4(a2+2ab)+2(2a2−ab),其中a=2,b=−1. 解方程: (1)4−x=5(2+x) (2)2x−13−x+34=1 为了解某校“阅读工程”的开展情况,市教育局从该校初中生中随机抽取了150名学生进行了阅读情况的问卷调查,绘制了如图不完全的统计图: 根据上述统计图提供的信息,解答下列问题: (1)初中生每天阅读时间在哪一段的人数最多?每天阅读时间在B段的扇形的圆心角是多少度? (2)若将写读后感、笔记积累、画圈点读三种方式称为有记忆阅读.求笔记积累人数占有记忆阅读人数的百分比,并补全条形统计图. 第17页 共18页 ◎ 第18页 共18页 已知∠AOB=50∘,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数. 阅读理解: 把几个数用大括号围起来,中间用逗号断开,如:{3, 4},{−3, 6, 8, 18},我们称之为集合,其中大括号内的数称其为集合的元素.如果一个集合满足:只要其中有一个元素a,使得−2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3, −2},因为−2×3+4=−2,−2恰好是这个集合的元素,所以{3, −2}是条件集合;例如:集合{−2, 9, 8},因为−2×(−2)+4=8,8恰好是这个集合的元素,所以{−2, 9, 8}是条件集合. (1)集合{−4, 12}________条件集合;集合{12, −53, 223}________条件集合(填“是”或“不是”). (2)若集合{8, 10, n}是条件集合,求n的所有可能值. 目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表: 进价(元/只) 售价(元/只) 甲型 25 30 乙型 45 60 (1)如何进货,进货款恰好为46000元? (2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折? 在数轴上,点M、N表示的数分别为a、b,我们把a、b之差的绝对值叫做点M、N之间的距离,即MN=|a−b|.已知数轴上三点A、O、B表示的数分别为−3,0,1,点P为数轴上任意一点,其表示的数为x. (1)如果点P到点A、点B的距离相等,那么x=________; (2)当x是多少时,点P到点A、点B的距离之和是6; (3)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动,点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动几秒时,点P到点E、点F的距离相等. 第17页 共18页 ◎ 第18页 共18页 参考答案与试题解析 2019-2020学年山东省济南市章丘区七年级(上)期末数学试卷 一、选择题(本大题共12小题,每小题4分,共48分) 1. 【答案】 A 【考点】 有理数大小比较 【解析】 有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可. 【解答】 ∵ −3<−2.5<0<2, ∴ 在−3,−2.5,2,0这四个数中,最小的数是−3. 2. 【答案】 C 【考点】 几何体的展开图 【解析】 根据正方体展开图的11种形式对各小题分析判断即可得解. 【解答】 A、是“凹字形”,不是正方体展开图; B、左边4个正方形是“田字形”,不是正方体展开图; C、符合正方体展开图; D、折叠后有两个正方形重合,不是正方体展开图. 3. 【答案】 C 【考点】 科学记数法--表示较大的数 【解析】 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数. 【解答】 将384000用科学记数法表示为:3.84×105. 4. 【答案】 D 【考点】 全面调查与抽样调查 【解析】 根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答. 【解答】 A、对“神舟十一号”运载火箭发射前零部件质量情况的调查,适合采用全面调查; B、对某地区现有的16名百岁以上老人睡眠时间的调查,适合采用全面调查; C、对某校九年级三班学生视力情况的调查,适合采用全面调查; D、对某市场上某一品牌电脑使用寿命的调查,适合采用抽样调查; 5. 【答案】 B 【考点】 列代数式 【解析】 根据金额=单价×重量,路程=速度×时间,等边三角形周长=边长×3,两位数的表示=十位数字×10+个位数字进行分析即可. 【解答】 A、若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额,说法正确; B、若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数,说法错误; C、若一个人骑自行车的速度为a千米/时,则3a表示他3小时骑行的路程,说法正确; D、若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长,说法正确; 6. 【答案】 A 【考点】 多项式的概念的应用 单项式的概念的应用 【解析】 根据多项式与单项式的概念即可判断. 【解答】 A、单项式−x3y2的系数是−1,故此选项正确; B、a2b2π2是单项式,故此选项错误; C、−2π2x3y的次数是4,故此选项错误; D、3x2−y+5xy2是二次三项式,故此选项错误. 7. 【答案】 C 【考点】 列代数式求值方法的优势 【解析】 此题考查了代数式的求值与有理数的混合运算. 【解答】 解:A.x=3、y=3时,输出结果为32+2×3=15,不符合题意; B.x=−4、y=−2时,输出结果为(−4)2−2×(−2)=20,不符合题意; C.x=2、y=4时,输出结果为22+2×4=12,符合题意; D.x=4、y=2 第17页 共18页 ◎ 第18页 共18页 时,输出结果为42+2×2=20,不符合题意. 故选C. 8. 【答案】 B 【考点】 角平分线的定义 角的计算 【解析】 先根据平角的定义求出∠BOC=140∘,再由OD平分∠BOC,根据角平分线的定义求出∠COD=12∠BOC=70∘,即可求出∠DOE=20∘. 【解答】 ∵ ∠AOC=40∘, ∴ ∠BOC=180∘−∠AOC=140∘, ∵ OD平分∠BOC, ∴ ∠COD=12∠BOC=70∘, ∵ ∠COE=90∘, ∴ ∠DOE=90∘−70∘=20∘. 9. 【答案】 B 【考点】 一元一次方程的应用——其他问题 一元一次方程的应用——工程进度问题 【解析】 设甲商品的单价为6x元,则乙商品的单价为5x元,丙商品的单价为4x元,根据甲商品比丙商品的单价多12元,即可得出关于x的一元一次方程,解之即可得出x值,再将三种商品的单价相加即可得出结论. 【解答】 设甲商品的单价为6x元,则乙商品的单价为5x元,丙商品的单价为4x元, 依题意,得:6x−4x=12, 解得:x=6, ∴ 6x+5x+4x=90. 10. 【答案】 D 【考点】 由实际问题抽象出一元一次方程 【解析】 设AE=xcm,观察图形结合小长方形的长不变,即可得出关于x的一元一次方程,此题得解. 【解答】 设AE=xcm, 依题意,得:8+2x=x+(16−3x). 11. 【答案】 C 【考点】 比较线段的长短 【解析】 由已知条件可知,EC+FD=m−n,又因为E是AC的中点,F是BD的中点,则AE+FB=EC+FD,故AB=AE+FB+EF可求. 【解答】 由题意得,EC+FD=m−n ∵ E是AC的中点,F是BD的中点, ∴ AE+FB=EC+FD=EF−CD=m−n 又∵ AB=AE+FB+EF ∴ AB=m−n+m=2m−n 12. 【答案】 D 【考点】 规律型:图形的变化类 规律型:数字的变化类 有理数的混合运算 规律型:点的坐标 【解析】 根据题目的例子,可以运用类比的思想求出所求式子的值. 【解答】 设S=1+4+42+43+...+42019, 则4S=4+42+43+...+42020, 则4S−S=42020−1, 3S=42020−1, 故S=42020−13, 二.填空题(本大题共6小题,每小题4分,共24分) 【答案】 20 【考点】 列代数式求值 【解析】 首先把4a2+6b+8化成2(2a2+3b)+8,然后把2a2+3b=6代入,求出算式的值是多少即可. 【解答】 第17页 共18页 ◎ 第18页 共18页 当2a2+3b=6时, 4a2+6b+8 =2(2a2+3b)+8 =2×6+8 =12+8 =20 【答案】 7 【考点】 方程的解 【解析】 使方程左右两边相等的未知数的值是该方程的解.将方程的解代入方程可得关于a的一元一次方程,从而可求出a的值. 【解答】 把x=5代入方程ax−8=20+a 得:5a−8=20+a, 解得:a=7. 【答案】 8 【考点】 条形统计图 【解析】 根据题意和统计图可知骑车的人数有12人占总数的30%,从而可以得到调查的学生总数,进而可以得到步行的学生人数. 【解答】 由题意可得, 调查的学生数为:12÷30%=40, 故该班步行上学的学生有:40−20−12=8(人), 【答案】 8 【考点】 合并同类项 【解析】 由两个单项式2xm−3y5与−3x2yn+2的和是单项式就得出它们是同类项,由同类项的定义可求得m和n的值,再代入计算即可求解. 【解答】 ∵ 2xm−3y5与−3x2yn+2的和是单项式, ∴ 2xm−3y5与−3x2yn+2是同类项, ∴ m−3=2,n+2=5, ∴ m=5,n=3, ∴ m+n=5+3=8. 【答案】 7.5 【考点】 两点间的距离 【解析】 根据点C在线段AB上,且AC=13BC,可得BC=3AC,再根据M为BC的中点,即可求得AM的长. 【解答】 如图, ∵ 点C在线段AB上, AC=13BC,即BC=3AC, ∴ AC+BC=AB=12 即4AC=12 AC=3 ∴ BC=9 ∵ M为BC的中点, ∴ CM=12BC=4.5 ∴ AM=AC+CM=7.5cm. 【答案】 21 【考点】 一元一次方程的应用——其他问题 一元一次方程的应用——工程进度问题 【解析】 先根据其每一行、每一列以及两条对角线上的三个数之和都相等,寻找具有已知量最多且含有公共未知量的行或列,只能是4−1+a=d+3+a,此时可解得d=0;再以4+b+0=b+3+c为等式,可知c=1,依此类推求出各字母代表的值即可解答. 【解答】 依题意知4−1+a=d+3+a, 解得d=0; 又∵ 4+b+0=b+3+c为等式, ∴ c=1. 又4−1+a=a+1+f, ∴ f=2, ∴ a=6,b=5,e=7, ∴ a+b+c+d+e+f=6+5+1+0+7+2=21. 三、解答题(本大题共9小题,共78分) 【答案】 原式=−9−12+9=−12; 原式=−2ab+3a−4a+2b+2ab=−a+2b. 【考点】 整式的加减 有理数的混合运算 【解析】 (1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值; (2)原式去括号合并即可得到结果. 【解答】 第17页 共18页 ◎ 第18页 共18页 原式=−9−12+9=−12; 原式=−2ab+3a−4a+2b+2ab=−a+2b. 【答案】 【考点】 作图-三视图 由三视图判断几何体 【解析】 直接利用几何体的俯视图以及上面所标数字得出几何体的形状,进而得出其主视图和左视图. 【解答】 【答案】 原式=b2−4a2−8ab+4a2−2ab=b2−10ab, 当a=2,b=−1时,原式=1+20=21. 【考点】 整式的加减--化简求值 【解析】 原式去括号合并得到最简结果,把a与b的值代入计算即可求出值. 【解答】 原式=b2−4a2−8ab+4a2−2ab=b2−10ab, 当a=2,b=−1时,原式=1+20=21. 【答案】 去括号得:4−x=10+5x, 移项合并得:−6x=6, 解得:x=−1; 去分母得:4(2x−1)−3(x+3)=12, 去括号得:8x−4−3x−9=12, 移项合并得:5x=25, 解得:x=5. 【考点】 解一元一次方程 【解析】 (1)方程去括号,移项合并,把x系数化为1,即可求出解; (2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解. 【解答】 去括号得:4−x=10+5x, 移项合并得:−6x=6, 解得:x=−1; 去分母得:4(2x−1)−3(x+3)=12, 去括号得:8x−4−3x−9=12, 移项合并得:5x=25, 解得:x=5. 【答案】 根据题意得:150−(18+22+70)=40(人),笔记积累学生有40人, 根据扇形统计图得:初中生每天阅读时间不足1小时的人数最多; 阅读时间在B段的扇形圆心角为(1−10%−20%−40%)×360∘=108∘; 根据题意得:4018+40+22×100%=50%, 则笔记积累人数占有记忆阅读人数的百分比为50%,补全条形统计图,如图所示. 【考点】 条形统计图 扇形统计图 【解析】 (1)根据扇形统计图得出每天阅读时间在不足1小时的人数最多;由总学生数减去其中的求出笔记积累的学生数,求出B段占的百分比,乘以360即可得到结果; (2)求出笔记积累占写读后感、笔记积累、画圈点读三种方式总人数的百分比,补全条形统计图即可. 【解答】 根据题意得:150−(18+22+70)=40(人),笔记积累学生有40人, 根据扇形统计图得:初中生每天阅读时间不足1小时的人数最多; 阅读时间在B段的扇形圆心角为(1−10%−20%−40%)×360∘=108∘; 根据题意得:4018+40+22×100%=50%, 则笔记积累人数占有记忆阅读人数的百分比为50%,补全条形统计图,如图所示. 【答案】 第17页 共18页 ◎ 第18页 共18页 如图(1)射线OC在∠AOB的内部,(2)射线OC在∠AOB的外部 (1)设∠AOC、∠COB的度数分别为2x、3x,则2x+3x=50∘ ∴ x=10∘,∠AOC=2x=20∘,∠AOD=12×50∘=25∘ ∴ ∠COD=∠AOD−∠AOC=25∘−20∘=5∘; (2)设∠AOC、∠COB的度数分别为2x、3x,则∠AOB=3x−2x=x=50∘, ∴ ∠AOC=2x=100∘ ∠AOD=25∘ ∴ ∠COD=∠AOC+∠AOD=100∘+25∘=125∘. 【考点】 角的计算 角平分线的定义 【解析】 分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC、∠COB的度数分别为2x、3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,∠AOC、∠COB的度数分别为2x、3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论. 【解答】 如图(1)射线OC在∠AOB的内部,(2)射线OC在∠AOB的外部 (1)设∠AOC、∠COB的度数分别为2x、3x,则2x+3x=50∘ ∴ x=10∘,∠AOC=2x=20∘,∠AOD=12×50∘=25∘ ∴ ∠COD=∠AOD−∠AOC=25∘−20∘=5∘; (2)设∠AOC、∠COB的度数分别为2x、3x,则∠AOB=3x−2x=x=50∘, ∴ ∠AOC=2x=100∘ ∠AOD=25∘ ∴ ∠COD=∠AOC+∠AOD=100∘+25∘=125∘. 【答案】 是,是 ∵ 集合{8, 10, n}是条件集合, ∴ 若n=−2×8+4,则n=−12; 若n=−2×10+4,则n=−16; 若−2n+4=8,则n=−2; 若−2n+4=10,则n=−3; −2n+4=n,则n=43; ∴ 可得n的可能值有−12,−16,−2,−3,43. 【考点】 有理数的概念及分类 【解析】 (1)依据一个集合满足:只要其中有一个元素a,使得−2a+4也是这个集合的元素,这样的集合我们称为条件集合,即可得到结论; (2)分情况讨论:若n=−2×8+4,则n=−12;若n=−2×10+4,则n=−16;若−2n+4=8,则n=−2;若−2n+4=10,则n=−3. 【解答】 ∵ −4×(−2)+4=12, ∴ 集合{−4, 12}是条件集合; ∵ −53×(−2)+4=223, ∴ 集合{12, −53, 223}是条件集合. 故答案为:是;是; ∵ 集合{8, 10, n}是条件集合, ∴ 若n=−2×8+4,则n=−12; 若n=−2×10+4,则n=−16; 若−2n+4=8,则n=−2; 若−2n+4=10,则n=−3; −2n+4=n,则n=43; ∴ 可得n的可能值有−12,−16,−2,−3,43. 【答案】 购进甲型节能灯400只,购进乙型节能灯800只进货款恰好为46000元 乙型节能灯需打9折 【考点】 一元一次方程的应用——其他问题 一元一次方程的应用——工程进度问题 【解析】 (1)设商场购进甲型节能灯x只,则购进乙型节能灯(1200−x)只,根据甲乙两种灯的总进价为46000元列出一元一次方程,解方程即可; (2)设乙型节能灯需打a折,根据利润=售价-进价列出a的一元一次方程,求出a的值即可. 【解答】 设商场购进甲型节能灯x只,则购进乙型节能灯(1200−x)只, 由题意,得25x+45(1200−x)=46000 解得:x=400 购进乙型节能灯1200−x=1200−400=800只. 答:购进甲型节能灯400只,购进乙型节能灯800只进货款恰好为46000元. 设乙型节能灯需打a折, 0.1×60a−45=45×20%, 解得a=9, 答:乙型节能灯需打9折. 【答案】 −1 |=4,点P到点A,点B的距离之和是6, ∴ 点P在点A的左边时,−3−x+1−x=6, 解得x=−4, 点P在点B的右边时,x−1+x−(− =6, 第17页 共18页 ◎ 第18页 共18页 解得x=2, 综上所述,x=−4或2; ((1)设运动时间为t,点P表示的数为−3t,点E表示的数为−3−t,点F表示的数为1−4t, ∵ 点P到点E,点F的距离相等, ∴ |−3t−(−3−t)|=|−3t−(1−4t)|, ∴ −2t+3=t−1或−2t+3=1−t, 解得t=43或t=2 【考点】 一元一次方程的应用——其他问题 数轴 绝对值 一元一次方程的应用——工程进度问题 【解析】 (1)根据数轴上两点间的距离的表示列出方程求解即可; (2)根据AB的距离为4,小于6,分点P在点A的左边和点B的右边两种情况分别列出方程,然后求解即可; (3)设运动时间为t,分别表示出点P、E、F所表示的数,然后根据两点间的距离的表示列出绝对值方程,然后求解即可. 【解答】 (1)由题意得,|x−(−3)|=|x−1|, 解得x=−1. 第17页 共18页 ◎ 第18页 共18页查看更多