- 2021-04-21 发布 |
- 37.5 KB |
- 4页
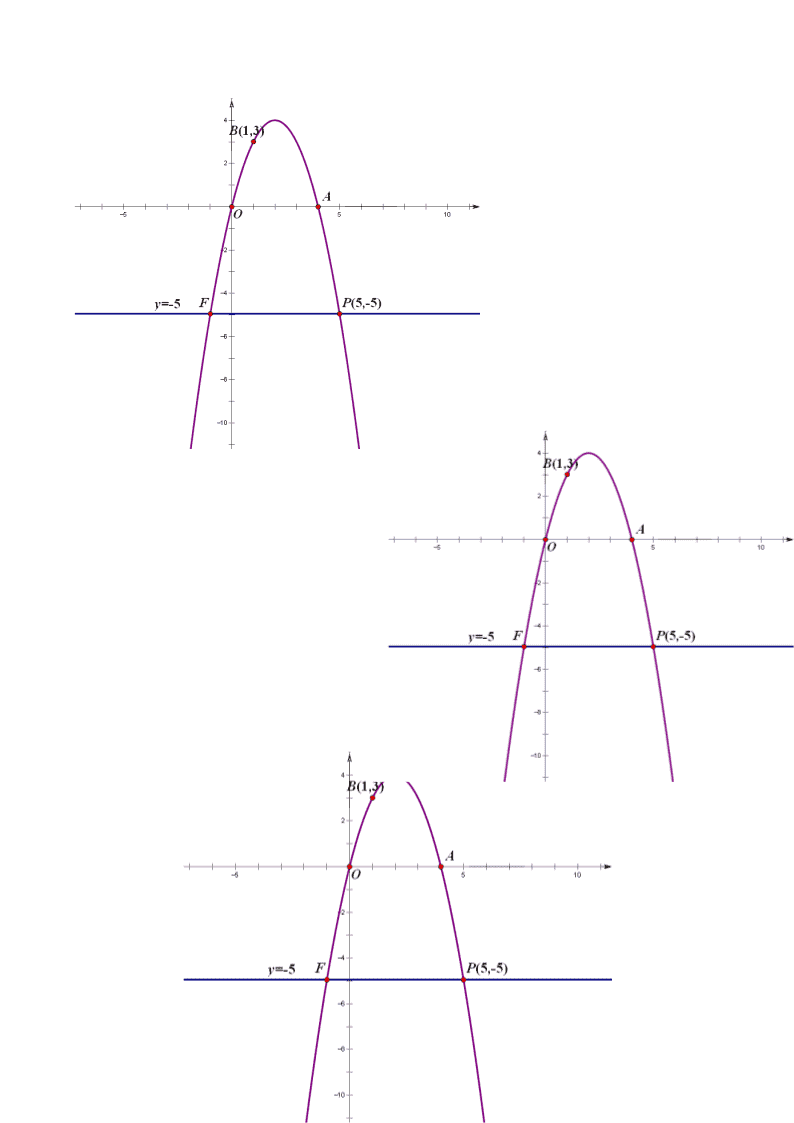
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
一个中考热点模型的拓展与应用学案
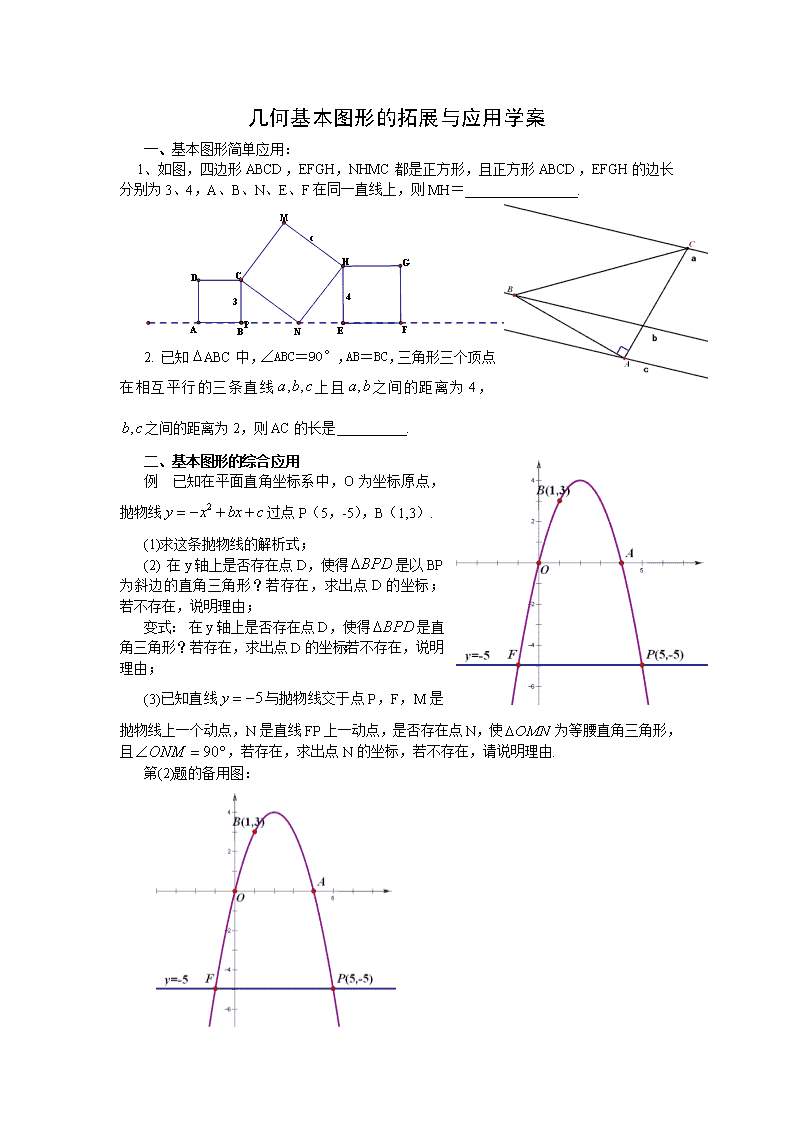
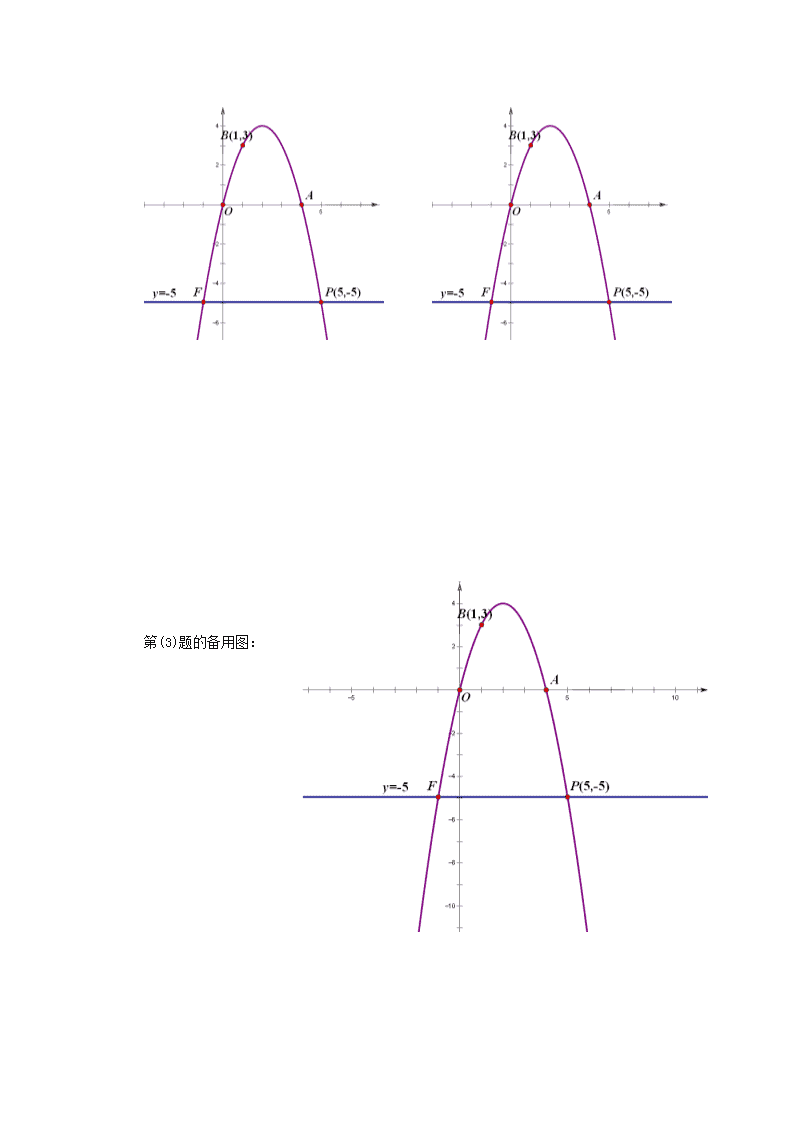
几何基本图形的拓展与应用学案 一、基本图形简单应用: 1、如图,四边形ABCD,EFGH,NHMC都是正方形,且正方形ABCD,EFGH的边长分别为3、4,A、B、N、E、F在同一直线上,则MH= . 2. 已知ABC中,∠ABC=90°,AB=BC,三角形三个顶点在相互平行的三条直线上且之间的距离为4, 之间的距离为2,则AC的长是 . 二、基本图形的综合应用 例 已知在平面直角坐标系中,O为坐标原点,抛物线过点P(5,-5),B(1,3). (1)求这条抛物线的解析式; (2) 在y轴上是否存在点D,使得是以BP为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由; 变式: 在y轴上是否存在点D,使得是直角三角形?若存在,求出点D的坐标;若不存在,说明理由; (3)已知直线与抛物线交于点P,F,M是抛物线上一个动点,N是直线FP上一动点,是否存在点N,使为等腰直角三角形,且,若存在,求出点N的坐标,若不存在,请说明理由. 第(2)题的备用图: 第(3)题的备用图: 【课外作业】: 1.矩形ABCD中,AB=4,BC=6,动点P从B沿BA方向向终点A以每秒1个单位的速度运动,同时动点Q从B点沿BC方向向终点C以每秒2个单位的速度运动,以线段PQ为折痕将 △BPQ对折,设对折后B点与点R重合,运动时间为t秒。 (1) t= 时,点R在AD边上; (2) t= 时,点R在矩形ABCD的对角线AC上。 2.如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B. (1)写出点B的坐标 ▲ ; (2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点. 若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 ▲ . O B C D查看更多