- 2021-04-20 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西省2016年中考数学卷
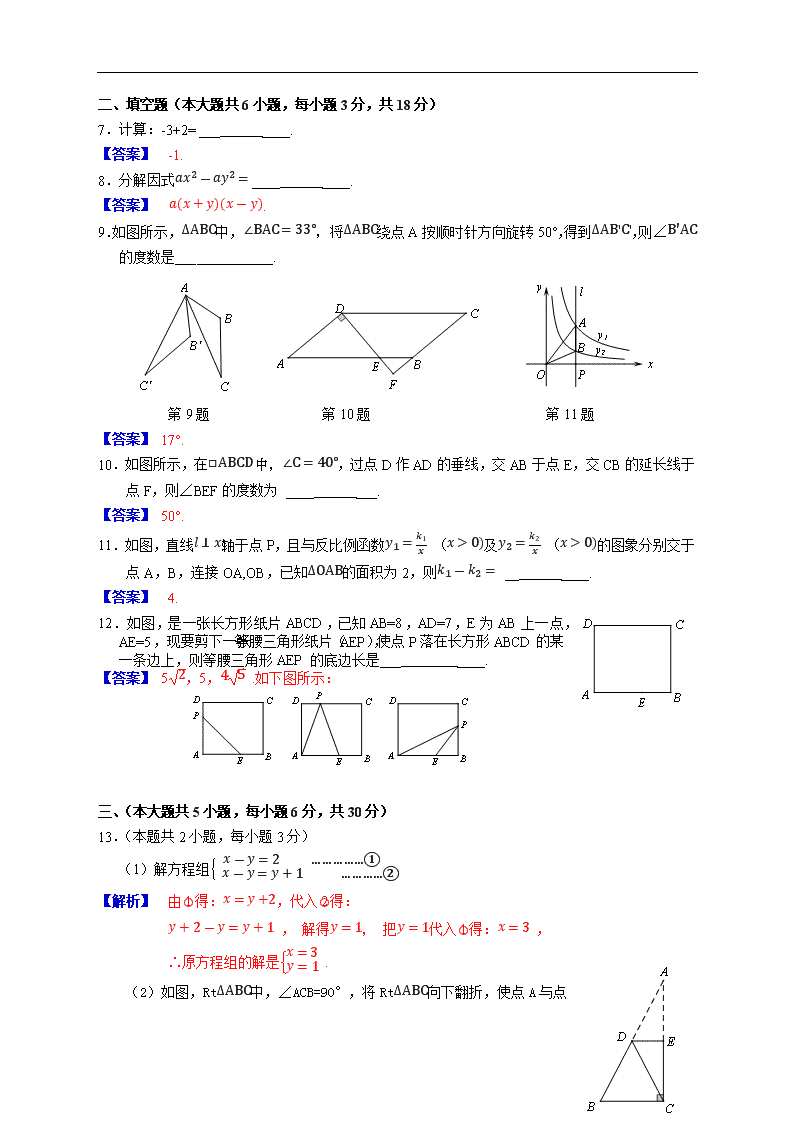
江西省2016年中等学校招生考试 数学试题卷(word解析版) (江西省 南丰县第二中学 方政昌) 说明:1.本卷共有六个大题,23个小题,全卷满分120分,考试时间120分钟. 2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分. 一、选择题(本大题共6个小题,每小题3分,共18分,每小题只有一个正确选项) 1.下列四个数中,最大的一个数是( ). A.2 B.3 C.0 D.-2 【答案】 A. 2.将不等式3x-2<1的解集表示在数轴上,正确的是( ). A. B. C. D. 【答案】 D. 3.下列运算正确的是是( ). A.a2+a2=a4 B.(-b2)3=-b6 C.2x∙2x2=2x3 D.(m-n)2=m2-n2 【答案】 B. 4.有两个完全相同的长方体,按下面右图方式摆放,其主视图是( ). A. B. C. D. 【答案】 C. 5.设α,β是一元二次方程x2+2x-1=0的两个根,则αβ的值是( ). A. 2 B. 1 C. -2 D. -1 【答案】 D. 6.如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为,,)的顶点都在网格上,被一个多边形覆盖的网格线中,竖直部分线段长度之和为m,水平部分线段长度之和为n,则这三个多边形满足m=n的是( ). A.只有 B.只有 C. D. 【答案】 C. 二、填空题(本大题共6小题,每小题3分,共18分) 7.计算:-3+2= ___ ____. 【答案】 -1. 8.分解因式ax2-ay2=____ ____. 【答案】 a(x+y)(x-y). 9.如图所示,∆ABC中,∠BAC=33°,将∆ABC绕点A按顺时针方向旋转50°,得到∆AB'C',则∠B'AC的度数是___ _____. 第9题 第10题 第11题 【答案】 17°. 10.如图所示,在□ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 ____ ___. 【答案】 50°. 11.如图,直线l⊥x轴于点P,且与反比例函数y1=k1x (x>0)及y2=k2x (x>0)的图象分别交于点A,B,连接OA,OB,已知∆OAB的面积为2,则k1-k2= __ ____. 【答案】 4. 12.如图,是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP 的底边长是___ ____. 【答案】 52,5,45 .如下图所示: 三、(本大题共5小题,每小题6分,共30分) 13.(本题共2小题,每小题3分) (1)解方程组x-y=2 ……………① x-y=y+1 …………② 【解析】 由得:x=y+2,代入得: y+2-y=y+1 , 解得y=1, 把y=1代入得:x=3 , ∴原方程组的解是x=3y=1 . (2)如图,Rt∆ABC中,∠ACB=90°,将Rt∆ABC向下翻折,使点A与点 C重合,折痕为DE,求证:DE∥BC. 【解析】 由折叠知:∆ADE≌∆CDE, ∴∠AED=∠CED , 又点A与点C重合, ∴∠AEC=180°, ∴∠AED=∠CED=90°, ∴∠EDC+∠ECD=90°, ∵∠ACB=90°,∴∠BCD+∠ECD=90°, ∴∠EDC=∠BCD, ∴DE∥BC. 14.先化简,再求值:(2x+3+13-x )÷xx2-9 ,其中x=6. 【解析】 原式=(2x+3+13-x )×x2-9x =(2x+3+13-x )×(x+3)(x-3)x = 2(x-3)x - x+3x = x-9x 把x=6代入得:原式 = 6-36=12 . 15.如图,过点A(2,0)的两条直线l1,l2 分别交 y 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=13. (1)求点B的坐标; (2)若∆ABC的面积为4,求l2的解析式. 【解析】 (1) 在Rt∆AOB中,OA2+OB2=AB2 , ∴ 22+OB2=(13)2 ∴ OB=3 ∴点B的坐标是(0,3) . (2) ∵S∆ABC=12 BC ∙OA ∴12 BC×2=4 ∴BC=4 ∴C(0,-1) 设l2 : y=kx+b , 把A(2,0),C(0,-1) 代入得: 2k+b=0 b=-1 ∴ k=12 b=-1 ∴ l2的解析式的解析式是y=12x-1 . 16.为了了解家长关注孩子成长方面的情况,学校开展了针对学生家长的“你最关注孩子哪方面 成长”的主题调查,调查设置了“健康安全”, “日常学习”, “习惯养成”, “情感品质”四个项目,并随机抽取甲,乙两班共100位学生家长进行调查,根据调查结果,绘制了如下不完整的条形统计图. (1)补全条形统计图; (2)若全校共有3600位家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和 指导? 【解析】(1)如下图所示: (2) (4+6) ÷100×3600=360 ∴约有360位家长最关心孩子“情感品质”方面的成长. (3) 没有确定答案,说的有道理即可. 17.如图,六个完全相同的小长方形拼成一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:仅用无刻度直尺,保留必要的画图痕迹. (1)在图(1)中画一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边; (2)在图(2)中画出线段AB的垂直平分线. 【解析】 如图所示: (1) ∠BAC=45º ; (2)OH是AB的垂直平分线. 四、(本大题共4小题,每小题8分,共32分) 18.如图,AB是⊙O的直径,点P是弦AC上一动点(不与A、C重合),过点P作PE⊥AB,垂足为E, 射线EP交 于点F,交过点C的切线于点D. (1)求证DC=DP (2)若∠CAB=30°,当F是 的中点时,判断以A、O、C、F为顶点的四边形是什么特殊四边形?说明理由; 【解析】 (1) 如图1 连接OC, ∵CD是⊙O的切线, ∴ OC⊥CD ∴∠OCD=90º, ∴∠DCA= 90º-∠OCA . 又PE⊥AB ,点D在EP的延长线上, ∴∠DEA=90º , ∴∠DPC=∠APE=90º-∠OAC. ∵OA=OC , ∴∠OCA=∠OAC. ∴∠DCA=∠DPC , ∴DC=DP. (2) 如图2 四边形AOCF是菱形. 图1 连接CF、AF, ∵F是 的中点,∴ ∴ AF=FC . ∵∠BAC=30º ,∴ =60º , 又AB是⊙O的直径, ∴ =120º, ∴ = 60º , ∴∠ACF=∠FAC =30º . ∵OA=OC, ∴∠OCA=∠BAC=30º, 图2 ∴⊿OAC≌⊿FAC (ASA) , ∴AF=OA , ∴AF=FC=OC=OA , ∴四边形AOCF是菱形. 19.如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成,闲置时鱼竿可收缩,完全收缩后,鱼竿的长度的长度即为第1节套管的长度(如图1所示),使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示),图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图,已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管都比前一节套管少4cm,完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm . (1)请直接写出第5节套管的长度; (2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值 . 图3 【解析】 (1) 第5节的套管的长是34cm . (注:50-(5-1)×4 ) (2) (50+46+…+14) -9x =311 ∴320-9x =311 , ∴x=1 ∴x 的值是1. 20.甲、乙两人利用扑克牌玩“10点”游戏,游戏规则如下: 将牌面数字作为“点数”,如红桃6的“点数”就是6(牌面点数与牌的花色无关); 两人摸牌结束时,将所得牌的“点数”相加 ,若“点数”之和小于或等于10,此时“点数”之和就是“最终点数”,若“点数”之和大于10,则“最终点数”是0; 游戏结束之前双方均不知道对方“点数”; 判定游戏结果的依据是:“最终点数”大的一方获胜,“最终点数”相等时不分胜负. 现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7. (1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为 . (2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌,请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的“最终点数”,并求乙获胜的概率. 【解析】 (1) P甲获胜=12 . (2) 如图: ∴所有可能的结果是(4,5)(4,6)(4,7)(5,4)(5,6)(5,7)(6,4)(6,5)(6,7) (7,4)(7,5)(7,6) 共12种. 甲 5 4 5 6 7 甲“最终点数” 9 10 11 12 乙 5 5 6 7 4 6 7 4 5 7 4 5 6 乙“最终点数” 10 11 12 9 11 12 9 10 12 9 10 11 获胜情况 乙胜 甲胜 甲胜 甲胜 甲胜 甲胜 乙胜 乙胜 平 乙胜 乙胜 平 ∴ P乙胜=512 21.如图1是一副创意卡通圆规,图2是其平面示意图,OA是 支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯 端点B可以绕点A旋转作出圆.已知OA=OB=10cm. (1)当∠AOB=18º时,求所作圆的半径;(结果精确到0.01cm) (2)保持∠AOB=18º不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等, 求铅笔芯折断部分的长度.(结果精确到0.01cm) (参考数据:sin9º≈0.1564,com9º≈0.9877º, sin18º≈0.3090, com18º≈0.9511,可使用科学计算器) 图1 图2 【解析】 (1) 图1,作OC⊥AB, ∵OA=OB, OC⊥AB,∴AC=BC, ∠AOC=∠BOC=12∠AOB=9°, 在Rt⊿AOC 中,sin∠AOC = ACOA , ∴AC≈0.1564×10=1.564, ∴AB=2AC=3.128≈3.13. ∴所作圆的半径是3.13cm. 图1 (2)图2,以点A为圆心,AB长为半径画弧,交OB于点C, 作AD⊥BC于点D; ∵AC=AB, AD⊥BC, ∴BD=CD, ∠BAD=∠CAD=12∠BAC, ∵∠AOB=18°,OA=OB ,AB=AC, ∴∠BAC=18°, ∴∠BAD=9°, 在Rt⊿BAD 中, sin∠BAD = BDAB , ∴BD≈0.1564×3.128≈0.4892, ∴BC=2BD=0.9784≈0.98 ∴铅笔芯折断部分的长度约为0.98cm. 图2 五、(本大题共10分) 22.【图形定义】 如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,⊿AOP为“叠弦三角形”. 【探究证明】 (1)请在图1和图2中选择其中一个证明:“叠弦三角形”(即⊿AOP)是等边三角形; (2)如图2,求证:∠OAB=∠OAE'. 【归纳猜想】 (3)图1、图2中“叠弦角”的度数分别为 , ; (4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”); (5)图n中,“叠弦角”的度数为 (用含n的式子表示). 【解析】 (1) 如图1 ∵四ABCD是正方形, 由旋转知:AD=AD',∠D=∠D'=90°, ∠DAD'=∠OAP=60° ∴∠DAP=∠D'AO , ∴⊿APD≌⊿AOD'(ASA) ∴AP=AO ,又∠OAP=60°, ∴⊿AOP是等边三角形. (2)如右图,作AM⊥DE于M, 作AN⊥CB于N. ∵五ABCDE是正五边形, 由旋转知:AE=AE',∠E=∠E'=108°, ∠EAE'=∠OAP=60° ∴∠EAP=∠E'AO , ∴⊿APE≌⊿AOE'(ASA) ∴∠OAE'=∠PAE. 在Rt⊿AEM和Rt⊿ABN中,∠M=∠N=90° ∠AEM=∠ABN=72° AE=AB ∴Rt⊿AEM≌Rt⊿ABN (AAS) ∴ ∠EAM=∠BAN , AM=AN. 在Rt⊿APM和Rt⊿AON中,AP=AOAM=AN ∴Rt⊿APM≌Rt⊿AON (HL). ∴∠PAM=∠OAN, ∴∠PAE=∠OAB ∴∠OAE'=∠OAB (等量代换). (3) 15°, 24° (4) 是 (5) ∠OAB=[(n-2) ×180°÷n-60°] ÷2=60°-180°n 六、(本大题共共12分) 23.设抛物线的解析式为y = a x2 , 过点B1 (1, 0 )作x轴的垂线,交抛物线于点A1 (1, 2 );过点B2 (1, 0 )作x轴的垂线,交抛物线于点A2 ,… ;过点Bn ((12)n-1 , 0 ) (n为正整数 )作x轴的垂线,交抛物线于点A n , 连接A n B n+1 , 得直角三角形A n B n B n+1 . (1)求a的值; (2)直接写出线段A n B n ,B n B n+1 的长(用含n的式子表示); (3)在系列Rt⊿A n B n B n+1 中,探究下列问题: 当n为何值时,Rt⊿A n B n B n+1 是等腰直角三角形? 设1≤k<m≤n (k , m均为正整数) ,问是否存在Rt⊿A k B k B k+1 与Rt⊿A m B m B m+1 相似?若存在,求出其相似比;若不存在,说明理由. 【解析】 (1) 把A(1 , 2)代入y=ax2 得: 2=a×12 , ∴a=2 . (2) AnBn=2×[(12)n-1]2 =23-2n BnBn+1 = (12)n-1-(12)n = 2-n (3) 若Rt⊿A n B n B n+1 是等腰直角三角形 ,则AnBn=BnBn+1 . ∴23-2n=2-n , ∴n=3. 若Rt⊿A k B k B k+1 与Rt⊿A m B m B m+1相似, 则 Ak BkAmBm= Bk Bk+1BmBm+1 或 Ak BkBmBm+1= Bk Bk+1AmBm , ∴ 23-2k23-2m= 2-k2-m 或 23-2k2-m= 2-k23-2m , ∴ m=k (舍去) 或 k+m=6 ∵m>k ,且m , k都是正整数,∴ m=4k=2 或 m=5k=1 , ∴ 相似比=2-k23-2m=2-223-2×4 =8 :1 ,或 2-k23-2m=2-123-2×5 =64 :1. ∴相似比是8:1或64:1查看更多