角平分线的性质导学案

角平分线的性质导学案

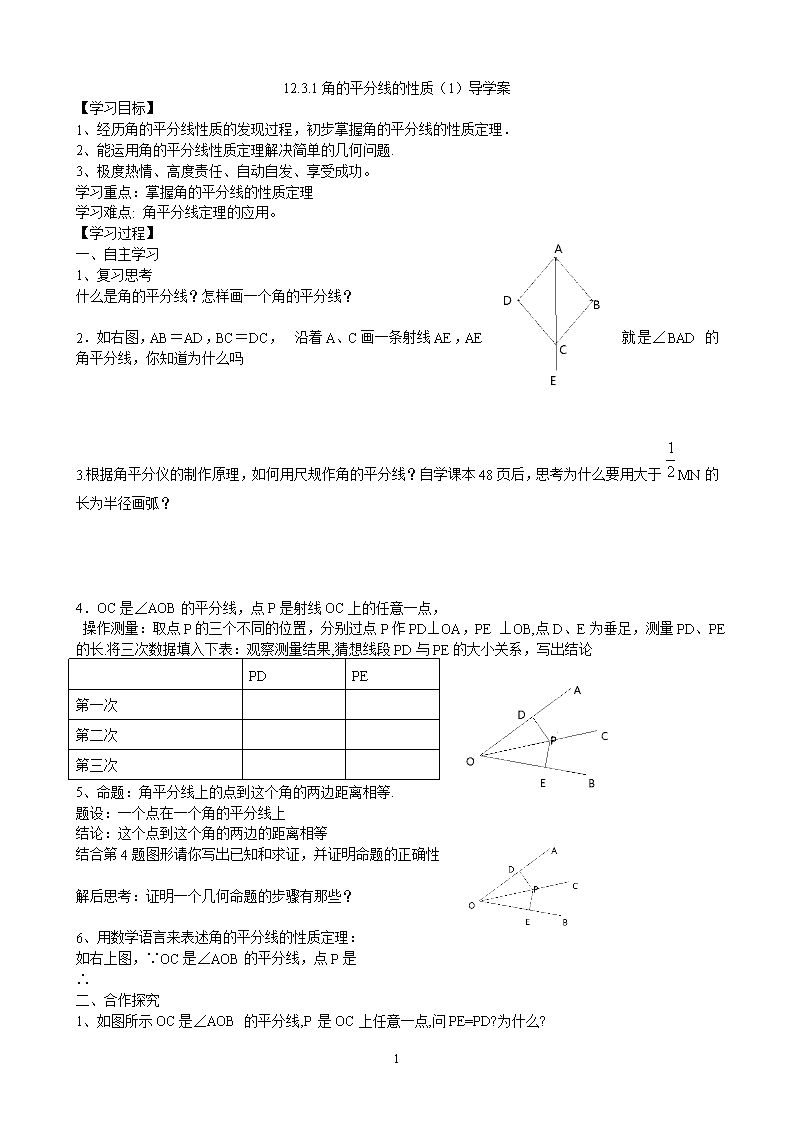
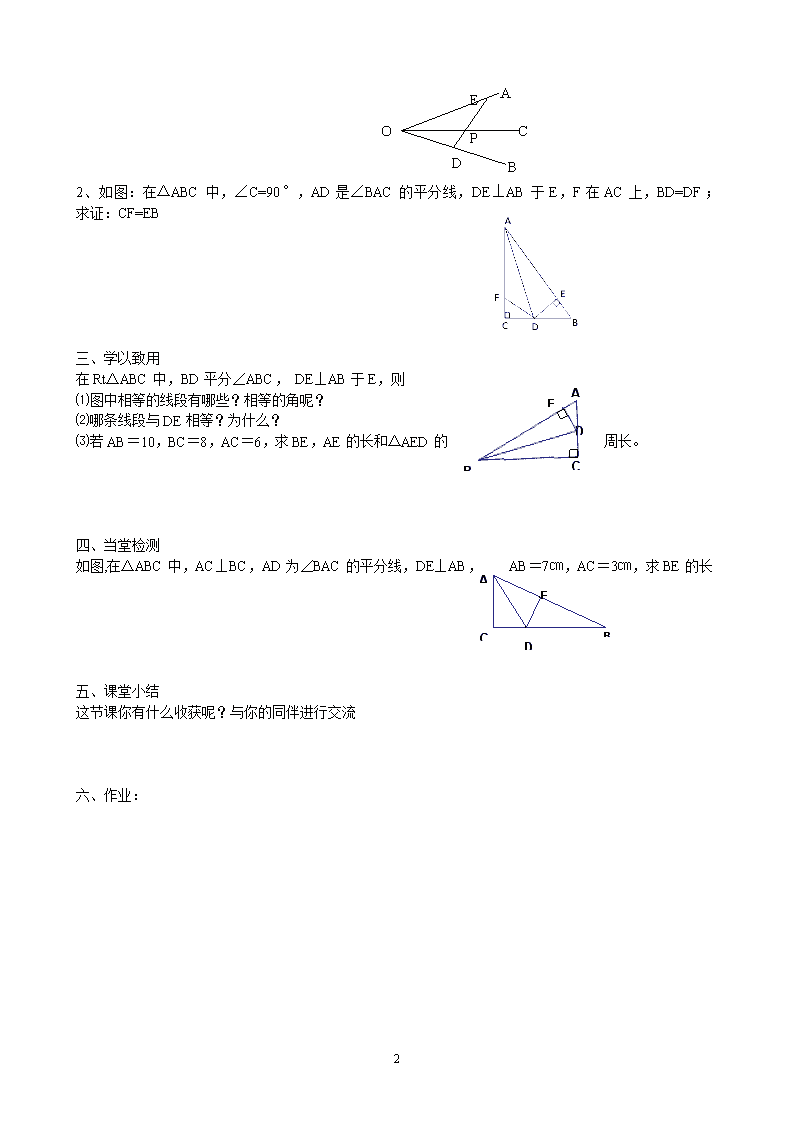
‎12.3.1角的平分线的性质（1）导学案 ‎【学习目标】‎ ‎1、经历角的平分线性质的发现过程，初步掌握角的平分线的性质定理．‎ ‎2、能运用角的平分线性质定理解决简单的几何问题.‎ ‎3、极度热情、高度责任、自动自发、享受成功。‎ 学习重点：掌握角的平分线的性质定理 学习难点: 角平分线定理的应用。‎ ‎【学习过程】‎ 一、自主学习 ‎1、复习思考 什么是角的平分线？怎样画一个角的平分线？‎ ‎2．如右图，AB＝AD，BC＝DC，　沿着A、C画一条射线AE，AE就是∠BAD的角平分线，你知道为什么吗 ‎3.根据角平分仪的制作原理，如何用尺规作角的平分线？自学课本48页后，思考为什么要用大于MN的长为半径画弧？‎ ‎4．OC是∠AOB的平分线，点P是射线OC上的任意一点，‎ ‎ 操作测量：取点P的三个不同的位置，分别过点P作PD⊥OA，PE ⊥OB,点D、E为垂足，测量PD、PE的长.将三次数据填入下表：观察测量结果,猜想线段PD与PE的大小关系，写出结论 ‎ PD PE 第一次 第二次 第三次 ‎5、命题：角平分线上的点到这个角的两边距离相等.‎ 题设：一个点在一个角的平分线上 结论：这个点到这个角的两边的距离相等 结合第4题图形请你写出已知和求证，并证明命题的正确性 解后思考：证明一个几何命题的步骤有那些？‎ ‎6、用数学语言来表述角的平分线的性质定理：‎ 如右上图，∵OC是∠AOB的平分线，点P是 ‎ ‎∴ ‎ 二、合作探究 ‎1、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为什么?‎ 2‎ O A B E D C P ‎2、如图：在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF； 求证：CF=EB 三、学以致用 E D C B A 在Rt△ABC中，BD平分∠ABC， DE⊥AB于E，则 ‎⑴图中相等的线段有哪些？相等的角呢？‎ ‎⑵哪条线段与DE相等？为什么？‎ ‎⑶若AB＝10，BC＝8，AC＝6，求BE，AE的长和△AED的周长。‎ 四、当堂检测 如图,在△ABC中，AC⊥BC，AD为∠BAC的平分线，DE⊥AB，AB＝7㎝，AC＝3㎝，求BE的E D C B A 长 五、课堂小结 这节课你有什么收获呢？与你的同伴进行交流 六、作业：‎ 2‎