- 2021-04-20 发布 |
- 37.5 KB |
- 9页

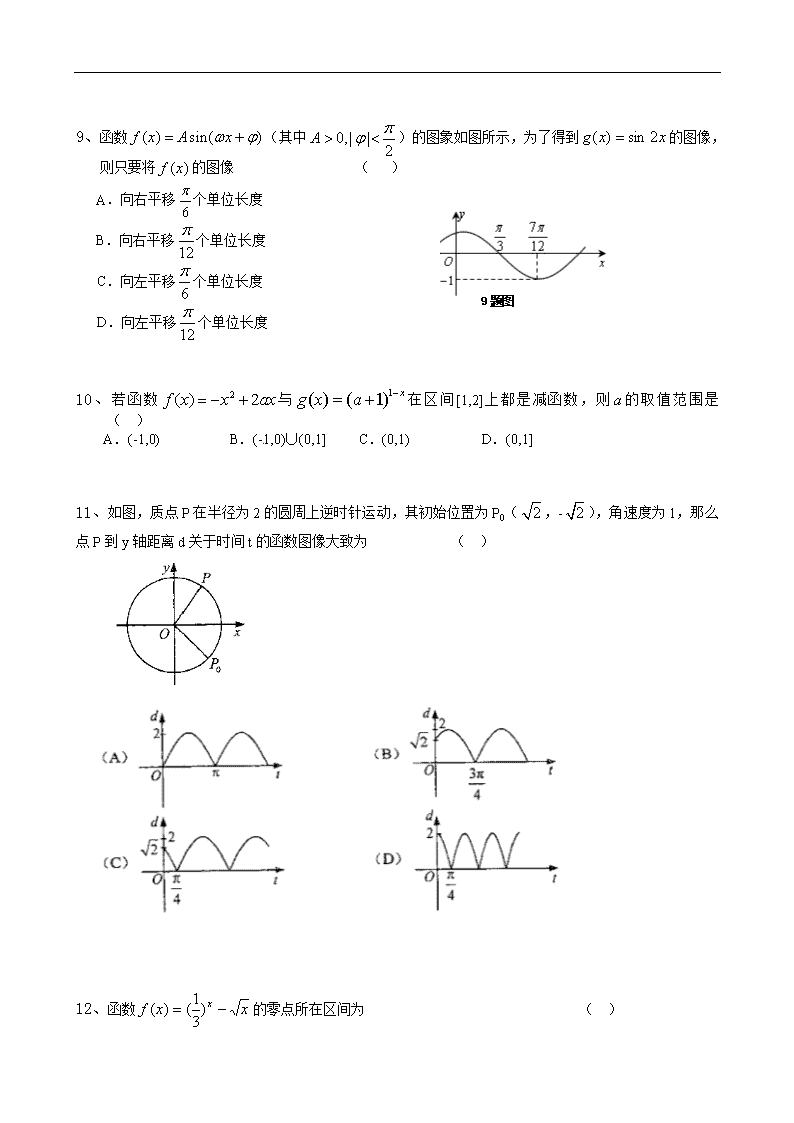

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
豫南九校2011—2012学年高三第二次联考
豫南九校2011—2012学年高三第二次联考 一、选择题 1、设集合 M = {x | x 2-x < 0},N = {x | | x | < 2},则 ( ) A.M∩N = Æ B.M∩N = M C.M∪N = M D.M∪N = R 2、= ( ) A. B. C. D. 3、已知:两个非零向量=(m-1,n-1),=(m-3,n-3),且与的夹角是钝角或直角,则m+n的取值范围是 ( ) A.(,3) B.(2,6) C. D. 4、如果等差数列中,+=12,那么= ( ) A.12 B. 24 C. 6 D. 4 5、下列函数中满足的是 ( ) A. B. C. D. 6、观察,,,由归纳推理可得:若定义在上的函数满足,记为的导函数,则= w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 ( ) A. B. C. D. 7、已知,则的大小关系为( ) A. B. C. D. 8、下面能得出△ABC为锐角三角形的条件是 ( ) A. B. C. D. 9、函数(其中)的图象如图所示,为了得到的图像,则只要将的图像 ( ) 9题图 A.向右平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向左平移个单位长度 10、若函数与在区间[1,2]上都是减函数,则的取值范围是 ( ) A.(-1,0) B.(-1,0)∪(0,1] C.(0,1) D.(0,1] 11、如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,-),角速度为1,那么点P到y轴距离d关于时间t的函数图像大致为 ( ) w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 12、函数的零点所在区间为 ( ) A. B. C. D.(1,2) 二、填空题 13、已知直线与函数的图象相切,则切点坐标为 。 14、已知正项等比数列满足,若存在两项使得,则的最小值是 。 15、函数的单调递增区间是 。 16、函数的定义域是 。 三、解答题 17、 数列{an}是等差数列,。 (1)求通项公式an (2)若,求数列的前n项和Sn 18、 如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M. (1)求证:DC是⊙O的切线; (2)求证:AM·MB=DF·DA. w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 19、 已知函数(). (1)当时,求函数在上的最大值; (2)当函数在单调时,求的取值范围; w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 20、 已知集合A={a,b,c},其中a,b,c是三个连续的自然数。如果a,b,c能够作为一个三角形的三边长,且该三角形的最大角是最小角的2倍,求所有满足条件的集合A。 w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 21、 某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出商品件数与商品单价的降低值x(单位:元,0≤x≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件 (1)将一个星期的商品销售利润表示成x的函数; (2)如何定价才能使一个星期的商品销售利润最大? 22、 已知 (1)求函数最小正周期; (2)当,求函数的最大值及取得最大值时的; 以下是答案 一、选择题 1、 B 2、 A 3、 B 4、 C 5、 D 6、 D 7、 C 8、 D 9、 A 10、 D 11、 B 12、 B 二、填空题 13、(1,e) 14、 15、 16、(-1,0) 三、解答题 17、 解:⑴, , ∴ ⑵由⑴知 ∴ ∴ w.w.^w.k.&s.5*u.c.#om高.考.资.源.网 18、 解:(I)连结OC,∴∠OAC=∠OCA,又∵CA是∠BAF的角平分线, ∴∠OAC=∠FAC, ∴∠FAC=∠ACO,∴OC∥AD. ∵CD⊥AF, ∴CD⊥OC,即DC是⊙O的切线. (Ⅱ)连结BC,在Rt△ACB中, CM⊥AB,∴CM2=AM·MB. 又∵DC是⊙O的切线,∴DC2=DF·DA. 易知△AMC≌△ADC,∴DC=CM, ∴AM·MB=DF·DA 19、 (1)时,, 函数在区间仅有极大值点,故这个极大值点也是最大值点, 故函数在最大值是, (2),令,则, 则函数在递减,在递增,由,, ,故函数在的值域为。 若在恒成立,即在恒成立, 只要,若要在在恒成立,即在恒成立, 只要。即的取值范围是。 20、 解法一:依题意,不妨设,对应的三个内角是 由正弦定理, 所以 由余弦定理, 即 化简,得: 所以,不合题意,舍去。 ,三角形的三边长为4,5,6. 可以验证此三角形的最大角是最小角的2倍。 故:A={4,5,6} 解法二:先考虑三角形应满足的第一个性质:三边是连续的自然数 ⑴三边长不可能是1,2,3,因为1+2=3而三角形的任何两边之和都大于第三边; ⑵如果三角形ABC的三边长分别是a=2,b=3,c=4 因为, 此三角形中,A是最小角,C是最大角,但是所以2A≠C从而三边 长分别是a=2,b=3,c=4不符合条件。 ⑶如果三角形ABC的三边长分别是a=3,b=4,c=5,此三角形是直角三角形,最大角是900,最小角不等于450,此三角形不满足条件。 ⑷如果三角形ABC的三边长分别是a=4,b=5,c=6,此时 ,, 因为,所以2A=C 故三边长分别是a=4,b=5,c=6满足条件。 ⑸当n>4时,三角形ABC的三边长分别是a=n,b=n+1,c=n+2时,三角形的最小角是A,最大角是C, · 随n的增大而减小,A随之增大,随n的增大而增大,C随之减小。由于n=4时有2A=C,所以n>4时不可能有2A=C。 · 总上可知,只有边长分别为4,5,6的三角形满足条件,即A={4,5,6} 21、 解:(1)设商品降价x元,则多卖出的商品数为kx2,在一个星期内商品的销售利润为 由题意得:24=k·22, ∴k=6, 所以 ⑵ 令得x=2或x=12, 2 12 — 0 + 0 — 单调递减 极小值 单调递增 极大值 单调递减 由上表可知当x=12时,取得极大值,而> ∴定价为18元时利润最大 22、 解: 函数最小正周期 又,所以,函数在上单调递增,在上单调递减 故当时取得最大值 查看更多