江西省南昌市进贤一中2019-2020学年高二下学期线上测试数学（理）试题

江西省南昌市进贤一中2019-2020学年高二下学期线上测试数学（理）试题

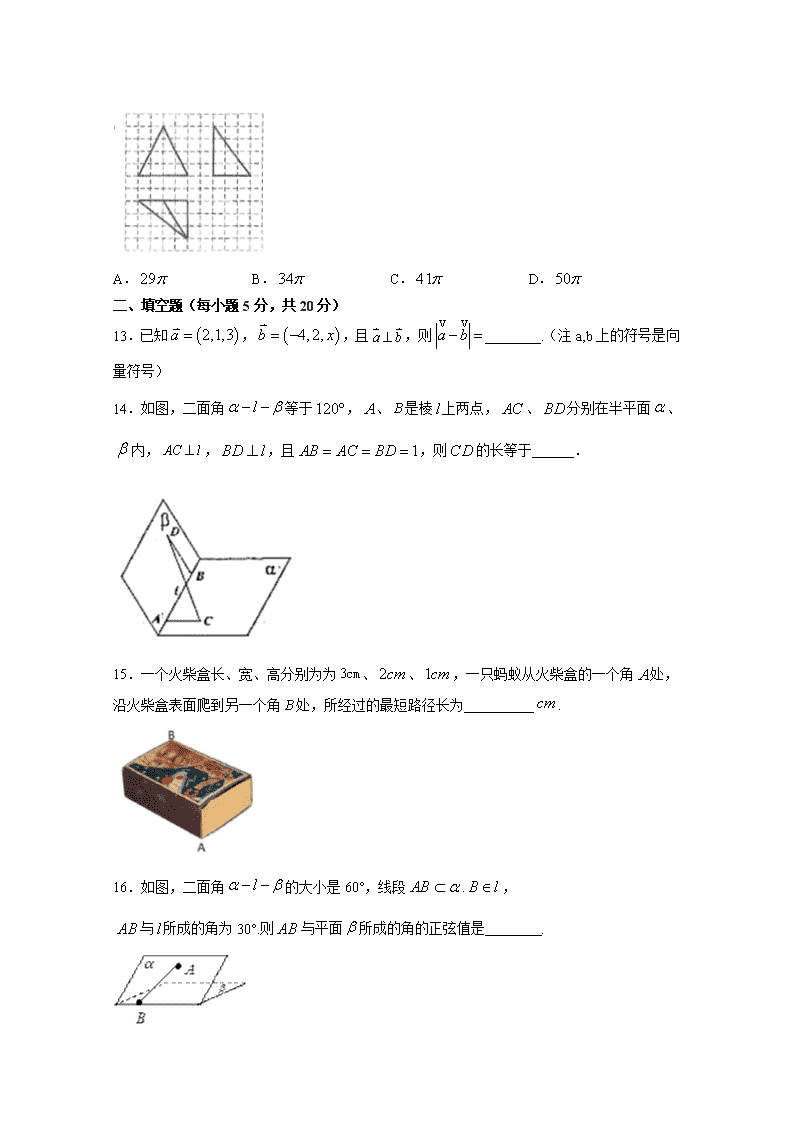
理科数学试卷 一、单选题（每小题5分，共60分）‎ ‎1．在空间直角坐标系中点关于平面对称点的坐标是（　　）‎ A．（1，﹣5，6） B．（1，5，﹣6）‎ C．（﹣1，﹣5，6） D．（﹣1，5，﹣6）‎ ‎2．下列说法中错误的是（ ）‎ A．正棱锥的所有侧棱长相等 B．圆柱的母线垂直于底面 C．直棱柱的侧面都是全等的矩形 ‎ D．用经过旋转轴的平面截圆锥，所得的截面一定是全等的等腰三角形 ‎3．如图所示的平面中阴影部分绕旋转轴（虚线）旋转一周，形成的几何体为（ ）‎ A．一个球 B．一个球挖去一个圆柱 C．一个圆柱 D．一个球挖去一个长方体 ‎4．已知某圆锥的轴截面为一等腰，其中，则该圆锥的体积为（ ）‎ A． B． C． D．‎ ‎5．已知正三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为（ ）‎ A． a2 B． a2 C． a2 D． a2‎ ‎6．如图，空间四边形OABC中，向量，，，且，，则等于( ) （题目OA,OB,OC,a,b,c,上面的符号是向量符号，选项a,b,c上面的r是向量符号）‎ A． B．‎ C． D．‎ ‎7．设是不同的直线，是不同的平面，则（ ）‎ A．若，，则 B．若，，，则 C．若，，，则 D．若，，，则 ‎8．在直三棱柱中，己知，，，则异面直线与所成的角为（ ）‎ A． B． C． D．‎ ‎9．已知，点在直线上运动，则当取得最小值时，点的坐标为（　　）（注OA,OB,OP,QA,QB上的符号是向量符号）‎ A． B． C． D．‎ ‎10．如图所示，在长方体ABCDA1B1C1D1中，AD＝AA1＝1，AB＝2，点E是棱AB的中点，则点E到平面ACD1的距离为(　　)‎ A． B． C． D．‎ ‎11．在正方体中，是棱的中点，则对角线与平面所成的角的正弦值为（ ）‎ A． B． C． D．‎ ‎12．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图则该几何体的外接球的表面积为 A． B． C． D．‎ 二、填空题（每小题5分，共20分）‎ ‎13．已知，，且，则________.（注a,b上的符号是向量符号）‎ ‎14．如图，二面角等于，、是棱上两点，、分别在半平面、内，，，且，则的长等于______．‎ ‎15．一个火柴盒长、宽、高分别为为、、，一只蚂蚁从火柴盒的一个角处，沿火柴盒表面爬到另一个角处，所经过的最短路径长为__________.‎ ‎16．如图，二面角的大小是60°，线段.，‎ 与所成的角为30°.则与平面所成的角的正弦值是 .‎ 三、解答题 ‎17．（10分）如图四边形ABCD为梯形，，求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积． ‎ ‎18．（12分）在三棱锥中，和是边长为的等边三角形，，分别是的中点. ‎ ‎（1）求证：平面； （2）求证：平面.‎ ‎19．（12分）如图，在三棱锥中，，分别为棱的中点，平面平面.‎ 求证： ‎ ‎（1）∥平面；‎ ‎（2）平面平面.‎ ‎20．（12分）如图，等腰梯形MNCD中，MD∥NC，MN＝MD＝2，∠CDM＝60°，E为线段MD上一点，且ME＝3，以EC为折痕将四边形MNCE折起，使MN到达AB的位置，且AE⊥DC ‎(1)求证:DE⊥平面ABCE;‎ ‎(2)求点A到平面DBE的距离 ‎21．（12分）如图，在四棱锥P−ABCD中，AB//CD，且.‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，求二面角A−PB−C的余弦值.‎ ‎22．（12分）如图，在三棱锥中，，，为的中点．‎ ‎（1）证明：平面；‎ ‎（2）若点在棱上，且二面角为，求与平面所成角的正弦值．‎ 数学参考答案 一，选择题：1.B 2 .C 3.B 4.C 5.D 6.C 7.D 8.C 9.C 10.C 11.C 12.B ‎ ‎1．B ‎【详解】‎ 在空间直角坐标系中，‎ 点P（1，5，6）关于平面xOy对称点Q的坐标是（1，5，﹣6）．‎ 故选：B．‎ ‎2．C ‎【详解】‎ 对于A,根据正棱锥的定义知,正棱锥的所有侧棱长相等,故A正确；‎ 对于B,根据圆柱是由矩形绕其一边旋转而成的几何体,可知圆柱的母线与底面垂直,故B正确；‎ 对于C,直棱柱的侧面都是矩形,但不一定全等,故C错误；‎ 对于D,圆锥的轴截面是全等的等腰三角形,故D正确.‎ 综上可知,错误的为C 故选:C ‎3．B ‎【解析】‎ ‎【分析】‎ 根据旋转体的定义，即可得出结论.‎ ‎【详解】‎ 由题意知形成的几何体为一个球挖去一个圆柱.‎ 故选:B.‎ ‎4．C ‎【详解】‎ 根据题意作出圆锥的轴截面图形如下图所示：‎ 其中为线段的中点，设底面圆的半径为，‎ 则，‎ 故圆锥的体积，‎ 故选：C.‎ ‎5．D ‎【详解】‎ 如图①②所示的实际图形和直观图.‎ 由斜二测画法可知，A′B′＝AB＝a，O′C′＝OC＝a，在图②中作C′D′⊥A′B′于D′，则C′D′＝O′C′＝a.所以S△A′B′C′＝A′B′·C′D′＝×a×a＝a2.‎ 故选：D.‎ ‎6．C ‎【详解】‎ 解：，，，，‎ ‎，故选：C。‎ ‎7．D ‎【详解】‎ 对于A，若，，则直线可以平行，也可以异面，所以A错误；‎ 对于B，因为不一定能成立，所以当，，时，不一定成立，所以B错误；‎ 对于C，若，，，则，或平面与平面相交，所以C错误；‎ 选项D：若，，，则成立，所以D正确.‎ 故选:D.‎ ‎8．C ‎【详解】‎ 连接，，如图：‎ 又，则为异面直线与所成的角.‎ 因为且三棱柱为直三棱柱，∴∴面，‎ ‎∴，‎ 又，，∴，‎ ‎∴，解得.‎ 故选C ‎【点睛】‎ ‎9．C ‎【详解】‎ ‎∵点Q在直线OP上运动，∴存在实数λ使得（λ，λ，2λ），‎ ‎∴，．‎ ‎∴（1﹣λ）（2﹣λ）+（2﹣λ）（1﹣λ）+（3﹣2λ）（2﹣2λ）‎ ‎＝6λ2﹣16λ+10＝6，‎ 当且仅当时，上式取得最小值，‎ ‎∴Q．‎ 故选C．‎ ‎10．C ‎【详解】‎ 以为坐标原点，直线分别为轴，建立空间直角坐标系，如图所示：‎ 设，则，,，，‎ 为的中点，则 ‎，，‎ 设平面的法向量为，则 ‎，即 可得 可取 点到面的距离为 故选 ‎11．C ‎【详解】‎ 如图,将正方体放入空间直角坐标系中,设边长为2,可得为,为,为,为,则,,,‎ 设平面的法向量,则,即,‎ 令,则,‎ 所以,‎ 则对角线与平面所成的角的正弦值为,‎ 故选：C ‎12．B ‎【详解】‎ 由三视图知（结合长方体）该几何体的实物图应为三棱锥，‎ 故球心肯定在长方体上、下底面的中心连线 上（设上、下底面的中心分别为 .‎ 记球心为点，设，则 ，‎ 结合三视图数据得，解得 ，则 ，‎ 故该几何体的外接球的表面积为 故选B.‎ ‎13．‎ ‎【详解】‎ 由题,因为,所以,即,‎ 所以,则,‎ 所以,‎ 故答案为：‎ ‎【点睛】‎ 本题考查已知向量垂直求坐标,考查坐标法向量的模 ‎14．2‎ ‎【详解】‎ ‎∵A、B是棱l上两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，‎ 又∵二面角α﹣l﹣β的平面角θ等于120°，且AB＝AC＝BD＝1，‎ ‎∴，60°，‎ ‎∴‎ 故答案为2．‎ ‎【点睛】‎ 本题考查的知识点是与二面角有关的立体几何综合题，其中利用，结合向量数量积的运算，是解答本题的关键．‎ ‎15．‎ ‎【详解】‎ 展开火柴盒所在长方体的表面，使AB在同一个矩形的对角线端点，‎ 这样的不同矩形共有三个，其对角线长度分别为：‎ 这种情况对角线长为，‎ 这种情况对角线长为，‎ 这种情况对角线长为 所以最短路径.‎ 故答案为：‎ ‎【点睛】‎ 此题考查求物体表面的最短路径，常用办法是展开成平面图形，利用两点之间线段最短求最短路径.‎ ‎16．‎ ‎【解析】‎ 试题分析：过点A作平面β的垂线，垂足为C，‎ 在β内过C作l的垂线．垂足为D，‎ 连接AD，有三垂线定理可知AD⊥l，‎ 故∠ADC为二面角α-l-β的平面角，为60°，‎ 又由已知，∠ABD=30°，‎ 连接CB，则∠ABC为AB与平面β所成的角 设AD=2，则AC=，CD=1‎ AB==4‎ ‎∴sin∠ABC==；‎ 故答案为．‎ 考点：本题主要考查二面角的计算．‎ 点评：基础题，本解法反映了求二面角方法的“几何法”—“一作、二证、三计算”．‎ ‎17．；体积．‎ ‎【解析】‎ ‎【分析】‎ 直角梯形绕直角腰旋转一周形成的是圆台，四分之一圆绕半径所在的直线旋转一周，形成的是半球，所以阴影部分绕旋转一周形成的是组合体，圆台挖去半球，，.‎ ‎【详解】‎ 圆中阴影部分是一个圆台，从上面挖出一个半球 S半球=×4π×22=8π S圆台侧=π×(2+5)×5=35π S圆台底=25π 故所求几何体的表面积S表＝8π+35π+25π＝68π ‎ V圆台=‎ V半球=.‎ 故所求几何体的体积V＝V圆台－V半球=.‎ ‎18．（1）答案见解析； （2）答案见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）要证平面，只需证，即可求得答案；‎ ‎（2）要证平面，只需证，，即可求得答案.‎ ‎【详解】‎ ‎（1）分别为的中点，‎ ‎.‎ 又平面，平面，‎ 平面.‎ ‎（2）∵，，‎ 为中点，，‎ ‎，.‎ 同理，，.‎ 又，‎ ‎.‎ ‎.‎ ‎.‎ ‎，，，‎ 平面.‎ ‎【点睛】‎ 本题主要考查了求证线面平行和线面垂直，解题关键是掌握线面平行判断定理和线面垂直判断定理，考查了分析能力，属于中档题.‎ ‎19．（1）详见解析；（2）详见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）证得MN∥BC，由线面平行的判定定理证明即可；（2）证得平面.‎ 由面面垂直的判定定理证明即可 ‎【详解】‎ ‎（1）∵分别为棱的中点，∴MN∥BC 又平面，∴∥平面.‎ ‎（2）∵，点为棱的中点，‎ ‎∴，‎ 又平面平面，平面平面，∴平面.‎ ‎∵平面，∴平面平面.‎ ‎【点睛】‎ 本题考查线面平行，面面垂直的判定，考查定理，是基础题 ‎20．（1）见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）等腰梯形中，MD＝4，CD＝MN＝2，利用余弦定理求出，由勾股定理得到CE DE，然后得到AE⊥平面CED，所以，从而可以得到DE⊥平面ABCE.（2）‎ 由（1）得到的CE⊥AE，可求出的面积，由DE⊥平面ABCE，求出三棱锥的体积，利用勾股定理得到的长，然后求出的面积，利用等体积转化，求出点A到平面DBE的距离.‎ ‎【详解】‎ ‎(1)等腰梯形MNCD中，MD∥NC，CD＝MD＝2‎ ‎∴MD＝4，CD＝MN＝2，‎ ‎△CED中，∠CDE＝60°，ED＝MD-EM＝1，‎ 则由余弦定理 ‎∴CE，∴CE2+ED2=CD2‎ ‎∴CEDE，∴CEME，CEAE 又AE⊥DC，DCCE＝C，‎ ‎∴AE⊥平面CED 而平面CED ‎∴，又，AECF＝E ‎∴DE⊥平面ABCE ‎(2)由(1)因CE⊥AE，则 因DE⊥平面ABCE，则 等腰梯形MCD中MD∥NC，MD＝4，‎ CD=MN＝2，CE⊥DE，DE＝1‎ 则NC=MD-2DE=2，故BC＝2，‎ 设点A到平面DBE的距离为h，因DE⊥平面ABCE 则，得h＝‎ 所以点A到平面DBE的距离为 ‎【点睛】‎ 本题考查线面垂直的性质和判定，等体积法求点到面的距离，属于中档题.‎ ‎21．（1）见解析；（2）.‎ ‎【解析】‎ ‎【详解】‎ ‎（1）由已知，得AB⊥AP，CD⊥PD．‎ 由于AB//CD ，故AB⊥PD ，从而AB⊥平面PAD．‎ 又AB 平面PAB，所以平面PAB⊥平面PAD．‎ ‎（2）在平面内作，垂足为，‎ 由（1）可知，平面，故，可得平面.‎ 以为坐标原点，的方向为轴正方向，为单位长，建立如图所示的空间直角坐标系.‎ 由（1）及已知可得，，，.‎ 所以，，，.‎ 设是平面的法向量，则 即 可取.‎ 设是平面的法向量，则 即可取.‎ 则，‎ 所以二面角的余弦值为.‎ ‎【名师点睛】‎ 高考对空间向量与立体几何的考查主要体现在以下几个方面：‎ ‎①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；‎ ‎②求直线与平面所成的角，关键是转化为直线的方向向量和平面的法向量的夹角；‎ ‎③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.‎ ‎22．（1）见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)根据等腰三角形性质得PO垂直AC，再通过计算，根据勾股定理得PO垂直OB，最后根据线面垂直判定定理得结论;(2)根据条件建立空间直角坐标系，设立各点坐标，根据方程组解出平面PAM一个法向量，利用向量数量积求出两个法向量夹角，根据二面角与法向量夹角相等或互补关系列方程，解得M坐标，再利用向量数量积求得向量PC与平面PAM法向量夹角，最后根据线面角与向量夹角互余得结果.‎ ‎【详解】‎ ‎（1）因为，为的中点，所以，且.‎ 连结.因为，所以为等腰直角三角形，‎ 且，.‎ 由知.‎ 由知平面.‎ ‎（2）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系.‎ 由已知得取平面的法向量.‎ 设，则.‎ 设平面的法向量为.‎ 由得，可取，‎ 所以.由已知得.‎ 所以.解得（舍去），.‎ 所以.又，所以.‎ 所以与平面所成角的正弦值为.‎ ‎【点睛】‎ 利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.‎