2019年河南省信阳市潢川县中考数学一模试卷（含答案解析）

2019年河南省信阳市潢川县中考数学一模试卷（含答案解析）

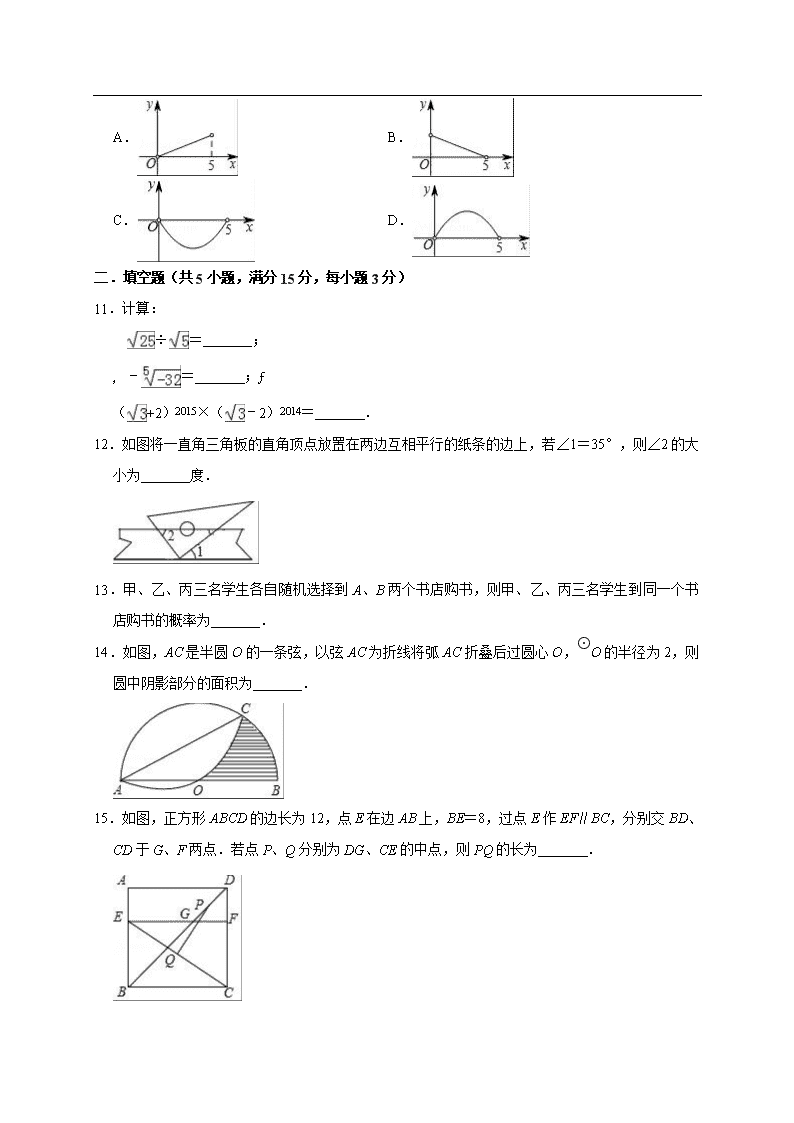
2019 年河南省信阳市潢川县中考数学一模试卷 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1．若实数 a、b 互为相反数，则下列等式中成 立的是（ ） A．a﹣b＝0 B．a+b＝0 C．ab＝1 D．ab＝﹣1 2．为庆祝首个“中国农民丰收节”，十渡镇西河村举办“西河稻作文化节”活动．西河水稻种植历 史悠久，因“色白粒粗，味极香美，七煮不烂”而享誉京城．已知每粒稻谷重约 0.000035 千克， 将 0.000035 用科学记数法表示应为（ ） A．35×10﹣6 B．3.5×10﹣6 C．3.5×10﹣5 D．0.35×10﹣4 3．如图是按 1：10 的比例画出的一个几何体的三视图，则该几何体的侧面积是（ ） A．200 cm2 B．600 cm2 C．100 π cm2 D．200 π cm2 4．郑州某中学在备考 2018 河南中考体育的过程中抽取该校九年级 20 名男生进 行立定跳远测试， 以便知道下一阶段的体育训练，成绩如下所示： 成绩（单位：米） 2.10 2.20 2.25 2.30 2.35 2.40 2.45 2.50 人数[来源:学科网 ZXXK] 2 3 2 4 5 2 1 1 则下列叙述正确的是（ ） A．这些运动员成绩的众数是 5 B．这些运动员成绩的中位数是 2.30 C．这些运动员的平均成绩是 2.25 D．这些运动员成绩的方差是 0.072 5 5．下列各式中与 是同类二次根式的是（ ） A． B． C． D． 6．如图，△AOB 是直角三角形，∠AOB＝90°，OB＝2OA，点 A 在反比例函数 y＝ 的图象上．若 点 B 在反比例函数 y＝ 的图象上，则 k 的值为（ ） A．﹣4 B．4 C．﹣2 D．2 7．若关于 x 的不等式组 无解，则 a 的取值范围是（ ） A．a≤﹣3 B．a＜﹣3 C．a＞3 D．a≥3 8．若 0＜m＜2，则关于 x 的一元二次方程﹣（x+m）（x+3m）＝3mx+37 根的情况是（ ） A．无实数根 B．有两个正根 C．有两个根，且都大于﹣3m D．有两个根，其中一根大于﹣m 9．如图，以矩形 ABOD 的两边 OD、OB 为坐标轴建立直角坐标系，若 E 是 AD 的中点，将△ABE 沿 BE 折叠后得到△GBE，延长 BG 交 OD 于 F 点．若 OF＝I，FD＝2，则 G 点的坐标为（ ） A．（ ， ） B．（ ， ） C．（ ， ） D．（ ， ） 10．如图，矩形 ABCD 中，AB＝3，BC＝5，点 P 是 BC 边上的一个动点（点 P 不与点 B、C 重合）， 现将△PCD 沿直线 PD 折叠，使点 C 落到点 C′处；作∠BPC′的角平分线交 AB 于点 E．设 BP ＝x，BE＝y，则下列图象中，能表示 y 与 x 的函数关系的图象大致是（ ） A． B． C． D． 二．填空题（共 5 小题，满分 15 分，每小题 3 分） 11．计算：  ÷ ＝ ； ‚﹣ ＝ ；ƒ （ +2）2015×（ ﹣2）2014＝ ． 12．如图将一直角三角板的直角顶点放置在两边互相平行的纸条的边上，若∠1＝35°，则∠2 的大 小为 度． 13．甲、乙、丙三名学生各自随机选择到 A、B 两个书店购书，则甲、乙、丙三名学生到同一个书 店购书的概率为 ． 14．如图，AC 是半圆 O 的一条弦，以弦 AC 为折线将弧 AC 折叠后过圆心 O， ⊙ O 的半径为 2，则 圆中阴影部分的面积为 ． 15．如图，正方形 ABCD 的边长为 12，点 E 在边 AB 上，BE＝8，过点 E 作 EF∥BC，分别交 BD、 CD 于 G、F 两点．若点 P、Q 分别为 DG、CE 的中点，则 PQ 的长为 ． 三．解答题（共 8 小题，满分 75 分） 16．先化简 ÷ ，然后从﹣1，0，2 中选一个合适的 x 的值，代入求值． 17．数学课上学习了圆周角的概念和性质：“顶点在圆上，两边与圆相交”，“同弧所对的圆周角 相等”，小明在课后继续对圆外角和圆内角进行了探究． 下面是他的探究过程，请补充完整： 定义概念：[来源:Zxxk.Com] 顶点在圆外，两边与圆相交的角叫做圆外角，顶点在圆内，两边与圆相交的角叫做圆内角．如图 1，∠M 为 所对的一个圆外角． （1）请在图 2 中画出 所对的一个圆内角； 提出猜想 （2）通过多次画图、测量，获得了两个猜想：一条弧所对的圆外角 这条弧所对的圆周角； 一条弧所对的圆内角 这条弧所对的圆周角；（填“大于”、“等于”或“小于”） 推理证明： （3）利用图 1 或图 2，在以上两个猜想中任选一个进行证明； 问题解决 经过证明后，上述两个猜想都是正确的，继续探究发现，还可以解决下面的问题． （4）如图 3，F，H 是∠CDE 的边 DC 上两点，在边 DE 上找一点 P 使得∠FPH 最大．请简述如 何确定点 P 的位置．（写出思路即可，不要求写出作法和画图） 18．在读书月活动中学校准备购买一批课外读物，为使课外读物满足同学们的需求，学校就”我最 喜爱的课外读物”从文 学、艺术、科普和其他四个类別进行了抽样调查（每位同学只选一类）．下 图是根据调查结果绘制的两幅不完整 的统计图． 请你根据统计图提供的信息，解答下列问题： （1）本次调查中，一共调查了 名同学； （2）条形统计图中 m＝ ，n＝ ； （3）扇形统计图中，艺术类读物所在扇形的圆心角是 度； （4）学校计划购买深外读物 8000 册，请根据样本数据，估计学校购买其他类读物多少册比较合 理？ 19．如图是小强洗漱时的侧面示意图，洗漱台（矩形 ABCD）靠墙摆放，高 AD＝80cm，宽 AB＝48cm， 小强身高 166cm，下半身 FG＝100cm，洗漱时下半身与地面成 80°（∠FGK＝80°），身体前 倾成 125°（∠EFG＝125°），脚与洗漱台距离 GC＝15cm（点 D，C，G，E 在同一直线上）．（cos80° ≈0.018，sin80°≈0.98， ≈1.414） （1）此时小强头部 E 点与地面 DK 相距多少？ （2）小强希望他的头部 E 恰好在洗漱盆 AB 的中点 O 的正上方，他应向前或后退多少？ 20．已知反比例函数的图象过点 A（﹣2，2）． （1）求函数的解析式．y 随 x 的增大而如何变化？[来源:学科网 ZXXK] （2）点 B（4，﹣2），C（3， ）和 D（ ）哪些点在图象上？ （3）画出这个函数的图象． 21．某物流公司承接 A、B 两种货物运输业务，已知 5 月份 A 货物运费单价为 50 元/吨，B 货物运费 单价为 30 元/吨，共收取运费 9500 元；6 月份由于油价上涨，运费单价上涨为：A 货物 70 元/吨， B 货物 40 元/吨；该物流公司 6 月承接的 A 种货物和 B 种数量与 5 月份相同，6 月份共收取运费 13000 元． （1）该物流公司 5 月份运输两种货物各多少吨？ （2）该物流公司预计 7 月份运输这两种货物 330 吨，且 A 货物的数量不大于 B 货物的 2 倍，在 运费单价与 6 月份相同的情况下，该物流公司 7 月份最多将收到多少运输费？ 22．如图 1，在 Rt△ABC 中，∠A＝90°，AB＝AC，点 D，E 分别在边 AB，AC 上，AD＝AE，连接 DC，点 M，P，N 分别为 DE，DC，BC 的中点． （1）观察猜想： 图 1 中，线段 PM 与 PN 的数量关系是 ，位置关系是 ； （2）探究证明： 把△ADE 绕点 A 逆时针方向旋转到图 2 的位置，连接 MN，BD，CE，判断△PMN 的形 状，并说明理由； （3）拓展延伸： 把△ADE 绕点 A 在平面内自 由旋转，若 AD＝4，AB＝10，请直接写出△PMN 面积的最 大值． 23．如图 1，抛物线 y＝ax2+bx+3 交 x 轴于点 A（﹣1，0） 和点 B（3，0）． （1）求该抛物线所对应的函数解析式； （2）如图 2，该抛物线与 y 轴交于点 C，顶点为 F，点 D（2，3）在该抛物线上． ① 求四边形 ACFD 的面积； ② 点 P 是线段 AB 上的动点（点 P 不与点 A、B 重合），过点 P 作 PQ⊥x 轴交该抛物线于点 Q， 连接 AQ、DQ，当△AQD 是直角三角形时，求出所有满足条件的点 Q 的坐标． 2019 年河南省信阳市潢川县中考数学一模试卷 参考答案与试题解析 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1．【分析】根据只有符号不同的两数叫做互为相反数解答． 【解答】解：∵实数 a、b 互为相反数， ∴a+b＝0． 故选：B． 【点评】本题考查了相反数的定义，是基础题，熟记概念是解题的关键． 2．【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时， 要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对 值＞1 时，n 是正数；当原数的绝对值＜1 时，n 是负数． 【解答】解：0.000035＝3.5×10﹣5， 故选：C． 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其中 1≤|a| ＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 3．【分析】首先判断出该几何体，然后计算其面积即可． 【解答】解：观察三视图知：该几何体为圆柱，高为 2，底面直径为 1， 侧面积为： π dh＝2× π ＝2 π ， ∵是按 1：10 的比例画出的一个几何体的三视图， ∴原几何体的侧面积＝100×2 π ＝200 π ， 故选：D． 【点评】本题考查了由三视图判断几何体及圆柱的计算，解题的关键是首先判断出该几何体． 4．【分析】根据方差、平均数、中位数和众数的计算公式和定义分别对每一项进行分析，即可得出 答案． 【解答】解：A、这些运动员成绩的众数是 2.35，错误； B、这些运动员成绩的中位数是 2.30，正确； C、这些运动员的平均成 绩是 2.30，错误； D、这些运动员成绩的方差不是 0.0725，错误；[来源:学_科_网 Z_X_X_K] 故选：B． 【点评】此题考查了方差、平均数、中位数和众数，熟练掌握定义和计算公式是本题的关键，平 均数平均数表示一组数据的平均程度．中位数是将一组数据从小到大（或从大到小）重新排列后， 最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量． 5．【分析】根据二次根式的性质把各个二次根式化简，根据同类二次根式的概念判断即可． 【解答】解：A． ＝3 ，与 是同类二次根式； B． ＝2 ，与 不是同类二次根式； C． ＝ ，与 不是同类二次根式； D． 与 不是同类二次根式； 故选：A． 【点评】本题考查的是同类二次根式的概念，把几个二次根式化为最简二次根式后，如果它们的 被开方数相同，就把这几个二次根式叫做同类二次根式． 6．【分析】要求函数的解析式只要求出 B 点的坐标就可以，过点 A，B 作 AC⊥x 轴，BD⊥x 轴，分 别于 C，D．根据条件得到△ACO∽△ODB，得到： ＝ ＝ ＝2，然后用待定系数法即可． 【解答】解：过点 A，B 作 AC⊥x 轴，BD⊥x 轴，分别于 C，D． 设点 A 的坐标是（m，n），则 AC＝n，OC＝m， ∵∠AOB＝90°， ∴∠AOC+∠BOD＝90°， ∵∠DBO+∠BOD＝90°， ∴∠DBO＝∠AOC， ∵∠BDO＝∠ACO＝90°， ∴△BDO∽△OCA， ∴ ＝ ＝ ， ∵OB＝2OA，[来源:Zxxk.Com] ∴BD＝2m，OD＝2n， 因为点 A 在反比例函数 y＝ 的图象上，则 mn＝1， ∵点 B 在反比例函数 y＝ 的图象上，B 点的坐标是（﹣2n，2m）， ∴k＝﹣2n•2m＝﹣4mn＝﹣4． 故选：A． 【点评】本题考查了反比例函数图象上点的坐标特征，相似三角形的判定和性质，求函数的解析 式的问题，一般要转化为求点的坐标的问题，求出图象上点的横纵坐标的积就可以求出反比例函 数的解析式． 7．【分析】利用不等式组取解集的方法，根据不等式组无解求出 a 的范围即可． 【解答】解：∵不等式组 无解， ∴a﹣4≥3a+2， 解得：a≤﹣3， 故选：A． 【点评】此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键． 8．【分析】先把方程化为一般式，再计算判别式的值得到△＝37（m2﹣4），然后根据 m 的范围得 到△＜0，从而根据判别式的意义可得到正确选项． 【解答】解：方程整理为 x2+7mx+3m2+37＝0， △＝49m2﹣4（3m2+37） ＝37（m2﹣4）， ∵0＜m＜2， ∴m2﹣4＜0， ∴△＜0， ∴方程没有实数根． 故选：A． 【点评】本题考查了抛物线与 x 轴的交点：把求二次函数 y＝ax2+bx+c（a，b，c 是常数，a≠0） 与 x 轴的交点坐标问题转化为解关于 x 的一元二次方程．也考查了判别式的意义． 9．【分析】连结 EF，作 GH⊥x 轴于 H，根据矩形的性质得 AB＝OD＝OF+FD＝3，再根据折叠的 性质得 BA＝BG＝3，EA＝EG，∠BGE＝∠A＝90°，而 AE＝DE，则 GE＝DE，于是可根据“HL” 证明 Rt△DEF≌Rt△GEF，得到 FD＝FG＝2，则 BF＝BG+GF＝5，在 Rt△OBF 中，利用勾股定 理计算出 OB＝2 ，然后根据△FGH∽△FBO，利用相似比计算出 GH＝ ，FH＝ ，则 OH ＝OF﹣HF＝ ，所以 G 点坐标为（ ， ）． 【解答】解：连结 EF，作 GH⊥x 轴于 H，如图， ∵四边形 ABOD 为矩形， ∴AB＝OD＝OF+FD＝1+2＝3， ∵△ABE 沿 BE 折叠后得到△GBE， ∴BA＝BG＝3，EA＝EG，∠BGE＝∠A＝90°， ∵点 E 为 AD 的中点， ∴AE＝DE， ∴GE＝DE， 在 Rt△DEF 和 Rt△GEF 中 ， ∴Rt△DEF≌Rt△GEF（HL）， ∴FD＝FG＝2， ∴BF＝BG+GF＝3+2＝5， 在 Rt△OBF 中，OF＝1，BF＝5， ∴OB＝ ＝2 ， ∵GH∥OB， ∴△FGH∽△FBO， ∴ ＝ ＝ ，即 ＝ ＝ ， ∴GH＝ ，FH＝ ， ∴OH＝OF﹣HF＝1﹣ ＝ ， ∴G 点坐标为（ ， ）． 故选：B． 【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和 大小不变，位置变化，对应边和对应角相等．也考查了坐标与图形的性质和相似三角形的判定与 性质． 10．【分析】连接 DE，根据折叠的性质可得∠CPD＝∠C′PD，再根据角平分线的定义可得∠BPE ＝∠C′PE，然后证明∠DPE＝90°，从而得到△DPE 是直角三角形，再分别表示 出 AE、CP 的 长度，然后利用勾股定理进行列式整理即可得到 y 与 x 的函数关系式，根据函数所对应的图象即 可得解． 【解答】解：如图，连接 DE，∵△PC′D 是△PCD 沿 PD 折叠得到， ∴∠CPD＝∠C′PD， ∵PE 平分∠BPC′， ∴∠BPE＝∠C′PE， ∴∠EPC′+∠DPC′＝ ×180°＝90°， ∴△DPE 是直角三角形，[来源:学科网] ∵BP＝x，BE＝y，AB＝3，BC＝5， ∴AE＝AB﹣BE＝3﹣y，CP＝BC﹣BP＝5﹣x， 在 Rt△BEP 中，PE2＝BP2+BE2＝x2+y2， 在 Rt△ADE 中，DE2＝AE2+AD2＝（3﹣y）2+52， 在 Rt△PCD 中，PD2＝PC2+CD2＝（5﹣x）2+32， 在 Rt△PDE 中，DE2＝PE2+PD2， 则（3﹣y）2+52＝x2+y2+（5﹣x）2+32， 整理得，﹣6y＝2x2﹣10x， 所以 y＝﹣ x2+ x（ 0＜x＜5）， 纵观各选项，只有 D 选项符合． 故选：D． 【点评】本题考查了动点问题的函数图象，勾股定理的应用，作出辅助线并证明得到直角三角形， 然后在多个直角三角形应用勾股定理是解题的关键． 二．填空题（共 5 小题，满分 15 分，每小题 3 分） 11．【分析】原式利用二次根式除法法则计算即可得到结果；原式利用五次方根定义计算即可得到 结果；原式变形后，逆用积的乘方运算法则计算即可得到结果． 【解答】解：原式＝ ＝ ；原式＝2；原式＝（ +2）[（ +2）（ ﹣2）]2014＝ +2． 故答案为： ；2； +2 【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 12．【分析】直接利用已知得出∠3 的度数，再利用平行线的性质得出答案． 【解答】解：∵将一直角三角板的直角顶点放置在两边互相平行的纸条的边上， ∴∠1+∠3＝90°，∠2 ＝∠3， ∵∠1＝35°， ∴∠3＝55°， ∴∠2＝∠3＝55°． 故答案为：55． 【点评】此题主要考查了平行线的性质，正确把握平行线的性质是解题关键． 13．【分析】首先根据题意画树状图，然后根据树状图即可求得所有等可能的结果与甲、乙、丙三 名学生在同一书店购书的情况数，然后根据概率公式求解即可求得答案．[来源:学*科*网 Z*X*X*K] 【解答】解：画树状图得： 由树状图知共有 8 种等可能结果，其中甲、乙、丙三名学生在同一书店购书的有 2 种情况， ∴甲、乙、丙三名学生到同一个书店购书的概率为 ＝ ， 故答案为： ． 【点评】此题考查了树状图法求概率．注意树状图法适合两步或两步以上完成的事件，树状图法 可以不重不漏的表示出所有等可能的结果，用到的知识点为：概率＝所求情况数与总情况数之比．[来 源:学|科|网] 14．【分析】过点 O 作 OE⊥AC，交 AC 于 D，连接 OC，BC，证明弓形 OC 的面积＝弓形 BC 的面 积，这样图中阴影部分的面积＝△OBC 的面积． 【解答】解：过点 O 作 OE⊥AC，交 AC 于 D，连接 OC，BC， ∵OD＝DE＝ OE＝ OA， ∴∠A＝30°， ∵AB 是 ⊙ O 的直径， ∴∠ACB＝90°， ∴∠B＝60°， ∵OB＝OC＝2， ∴△OBC 是等边三角形， ∴OC＝BC， ∴弓形 OC 面积＝弓形 BC 面积，[来源:Z.xx.k.Com] ∴阴影部分面积＝S△OBC＝ ×2× ＝ ． 故答案为： 【点评】本题考查了折叠问题、扇形的面积．解决本题的关键是把阴影部分的面积转化为△OBC 的面积． 15．【分析】根据题意作出合适的辅助线，利用三角形中位线定理、三角形的相似可以求得 PH 和 QH 的长，然后根据勾股定理即可求得 PQ 的长． 【解答】解：作 QM⊥EF 于点 M，作 PN⊥EF 于点 N，作 QH⊥PN 交 PN 的延长线于点 H，如右 图所示， ∵正方形 ABCD 的边长为 12，BE＝8，EF∥BC，点 P、Q 分别为 DG、CE 的中点， ∴DF＝4，CF＝8，EF＝12， ∴MQ＝4，PN＝2，MF＝6， ∵QM⊥EF，PN⊥EF，BE＝8，DF＝4， ∴△EGB∽△FGD， ∴ ， 即 ， 解得，FG＝4， ∴FN＝2， ∴MN＝6﹣2＝4， ∴QH＝4， ∵PH＝PN+QM， ∴PH＝6， ∴PQ＝ ＝ ， 故答案为：2 ． 【点评】本题考查三角形中位线定理、正方形的性质、勾股定理、三角形相似，解答本题的关键 是明确题意，找出所求问题需要的条件，利用数形结合的思想解答． 三．解答题（共 8 小题，满分 75 分） 16．【分析】先根据分式混合运算顺序和运算法则化简原式，再由分式有意义的条件选取合适的 x 的值代入计算可得． 【解答】解：原式＝ • ﹣ ＝ ﹣ ＝ ＝﹣ ， 当 x＝2 时，原式＝﹣ ． 【点评】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则 及分式有意义的条件． 17．【分析】（1）在 ⊙ O 内任取一点 M，连接 AM，BM； （2）观察图形，可知：一条弧所对的圆外角小于这条弧所对的圆周角；一条弧所对的圆内角大 于这条弧所对的圆周角，此问得解； （3）（i）BM 与 ⊙ O 相交于点 C，连接 AC，利用三角形外角的性质可得出∠ACB＝∠M+∠MAC， 进而可证出∠ACB＞∠M；（ii）延长 BM 交 ⊙ O 于点 C，连接 AC，利用三角形外角的性质可得 出∠AMB＝∠ACB+∠CAM，进而可证出∠AMB＞∠ACB； （4）由（2）的结论，可知：当过点 F，H 的圆与 DE 相切时，切点即为所求的点 P． 【解答】解：（1）如图 2 所示． （2）观察图形，可知：一条弧所对的圆外角小于这条弧所对的圆周角；一条弧所对的圆内角大 于这条弧所对的圆周角． 故答案为：小于；大于． （3）证明：（i）如图 1，BM 与 ⊙ O 相交于点 C，连接 AC． ∵∠ACB＝∠M+∠MAC， ∴∠ACB＞∠M； （ii）如图 4，延长 BM 交 ⊙ O 于点 C，连接 AC． ∵∠AMB＝∠ACB+∠CAM， ∴∠AMB＞∠ACB． （4）如图 3，当过点 F，H 的圆与 DE 相切时，切点即为所求的点 P． 【点评】本题考查了圆的综合应用以及三角形外角的性质，解题的关键是 ：（1）依照题意画出 图形；（2）观察图形，找出结论；（3）利用三角形外角的性质证出：一条弧所对的圆外角小于 这条弧所对的圆周角；一条弧所对的圆内角大于这条弧所对的圆周角；（4）利用（2）的结论找 出点 P 的位置． 18．【分析】（1）结合两个统计图，根据条形图得出文学类人数为：70，利用扇形图得出文学类所 占百分比为：35%，即可得出总人数； （2）利用科普类所占百分比为：30%，则科普类人数为：n＝200×30%＝60 人，即可得出 m 的 值； （3）根据圆心角计算公式，即可得到艺术类读物所在扇形的圆心角； （4）根据喜欢其他类读物人数所占的百分比，即可估计 6000 册中其他读物的数量． 【解答】解：（1）根据条形图得出文学类人数为：70，利用扇形图得出文学类所占百分比为： 35%， 故本次调查中，一共调查了：70÷35%＝200 人， 故答案为：200； （2）根据科普类所占百分比为：30%， 则科普类人数为：n＝200×30%＝60 人， m＝200﹣70﹣30﹣60＝40 人， 故 m＝40，n＝60； 故答案为：40，60； （3）艺术类读物所在扇形的圆心角是： ×360°＝72°， 故答案为：72； （4）由题意，得 8000× ＝1200（册）． 答：学校购买其他类读物 1200 册比较合理． 【点评】此题主要考查了条形图表和扇形统计图综合应用，将条形图与扇形图结合得出正确信息 求出调查的总人数是解题关键． 19．【分析】（1）过点 F 作 FN⊥DK 于 N，过点 E 作 EM⊥FN 于 M．求出 MF、FN 的值即可解决 问题； （2）求出 OH、PH 的值即可 判断； 【解答】解：（1）过点 F 作 FN⊥DK 于 N，过点 E 作 EM⊥FN 于 M． ∵EF+FG＝166，FG＝100， ∴EF＝66， ∵∠FGK＝80°， ∴FN＝100•sin80°≈98， ∵∠EFG＝125°， ∴∠EFM＝180°﹣125°﹣10°＝45°， ∴FM＝66•cos45°＝33 ≈46.53， ∴MN＝FN+FM≈144.5， ∴此时小强头部 E 点与地面 DK 相距约为 144.5cm． （2）过点 E 作 EP⊥AB 于点 P，延长 OB 交 MN 于 H． ∵AB＝48，O 为 AB 中点， ∴AO＝BO＝24， ∵EM＝66•sin45°≈46.53， ∴PH≈46.53， ∵GN＝100•cos80°≈17，CG＝15， ∴OH＝24+15+17＝56，OP＝OH﹣PH＝56﹣46.53＝9.47≈9.5， ∴他应向前 9.5cm． 【点评】本题考查直角三角形的应用，锐角三角函数等知识，解题的关键是学会添加常用辅助线， 构造直角三角形解决问题，属于中考常考题型．[来源:学科网] 20．【分析】（1）利用待定系数法求反比例函数的解析式； （2）根据反比例函数图象上点的坐标特征，将 B、C、D 三点分别代入进行验证即可； （3）根据该反比例函数所在的象限、以及该函数的单调性画出图象． 【解答】解：设该反比例函数的解析式为 y＝ （k≠0），则 2＝ ， 解得，k＝﹣4； 所以，该反比例函数的解析式为 y＝﹣ ； ∵﹣4＜0， ∴该反比例函数经过第二、四象限，且在每一象限内，y 随 x 的增大而增大； （2）由（1）知，该反比例函数的解析式为 y＝﹣ ，则 xy＝﹣4． ∵﹣2×4＝﹣8≠﹣4，3×（﹣ ）＝﹣4，2 ×（﹣ ）＝﹣4， ∴点 B（4，﹣2）不在该函数图象上，点 C（3， ）和 D（ ）在该函数图象上； （3）反比例函数的图象过点 A（﹣2，2），由（1）知，该反比例函数经过第二、四象限，且在 每一象限内，y 随 x 的增大而增大；所以其图象如图所示： 【点评】本题考查了反比例函数的图象与性质、待定系数法求反比例函数的解析式以及反比例函 数图象上点的坐标特征．经过函数的某点一定在该函数的图象上． 21．【分析】（1）设 A 种货物运输了 x 吨，设 B 种货物运输了 y 吨， 根据题意可得到一个关于 x 的不等式组，解方程组求解即可； （2）运费可以表示为 x 的函数，根据函数的性质，即可求解． 【解答】解：（1）设 A 种货物运输了 x 吨，设 B 种货物运输了 y 吨， 依题意得： ， 解之得： ． 答：物流公司月运输 A 种货物 100 吨，B 种货物 150 吨． （2）设 A 种货物为 a 吨，则 B 种货物为（330﹣a）吨， 依题意得：a≤（330﹣a）×2， 解得：a≤220， 设获得的利润为 W 元，则 W＝70a+40（330﹣a）＝30a+13200， 根据一次函数的性质，可知 W 随着 a 的增大而增大 当 W 取最大值时 a＝220， 即 W＝19800 元． 所以该物流公司 7 月份最多将收到 19800 元运输费． 【点评】本题考查二元一次方程组的应用和一元一次不等式组以及一次函数性质的应用，将现实 生活中的事件与数学思想联系起来，读懂题意列出方程组和不等式即可求解． 22．【分析】（1）利用三角形的中位线得出 PM＝ CE，PN＝ BD，进而判断出 BD＝CE，即可 得出结论，再利用三角形的中位线得出 PM∥CE 得出∠DPM＝∠DCA，最后用互余即可得出结论； （2）先判断出△ABD≌△ACE，得出 BD＝CE，同（1）的方法得出 PM＝ BD，PN＝ BD，即 可得出 PM＝PN，同（1）的方法即可得出结论； （3）方法 1：先判断出 MN 最大时，△PMN 的面积最大，进而求出 AN，AM，即可得出 MN 最 大＝AM+AN，最后用面积公式即可得出结论．方法 2：先判断出 BD 最大时，△PMN 的面积最大， 而 BD 最大是 AB+AD＝14，即可得出结论． 【解答】解：（1）∵点 P，N 是 BC，CD 的中点， ∴PN∥BD，PN＝ BD， ∵点 P，M 是 CD，DE 的中点， ∴PM∥CE，PM＝ CE， ∵AB＝AC，AD＝AE， ∴BD＝CE， ∴PM＝PN， ∵PN∥BD， ∴∠DPN＝∠ADC， ∵PM∥CE， ∴∠DPM＝∠DCA， ∵∠BAC＝90°， ∴∠ADC+∠ACD＝90°， ∴∠MPN＝∠DPM+∠DPN＝∠DCA+∠ADC＝90°， ∴PM⊥PN， 故答案为：PM＝PN，PM⊥PN； （2）△PMN 是等腰直角三角形． 由旋转知，∠BAD＝∠CAE， ∵AB＝AC，AD＝AE， ∴△ABD≌△ACE（SAS）， ∴∠ABD＝∠ACE，BD＝CE， 利用三角形的中位线得，PN＝ BD，PM＝ CE， ∴PM＝PN， ∴△PMN 是等腰三角形， 同（1）的方法得，PM∥CE， ∴∠DPM＝∠DCE， 同（1）的方法得，PN∥BD， ∴∠PNC＝∠DBC， ∵∠DPN＝∠DCB+∠PNC＝∠DCB+∠DBC， ∴∠MPN＝∠DPM+∠DPN＝∠DCE+∠DCB+∠DBC ＝∠BCE+∠DBC＝∠ACB+∠ACE+∠DBC ＝∠ACB+∠ABD+∠DBC＝∠ACB+∠ABC， ∵∠BAC＝90°， ∴∠ACB+∠ABC＝90°， ∴∠MPN＝90°， ∴△PMN 是等腰直角三角形； （3）方法 1：如图 2，同（2）的方法得，△PMN 是等腰直角三角形， ∴MN 最大时，△PMN 的面积最大， ∴DE∥BC 且 DE 在顶点 A 上面， ∴MN 最大＝AM+AN， 连接 AM，AN， 在△ADE 中，AD＝AE＝4，∠DAE＝90°， ∴AM＝2 ， 在 Rt△ABC 中，AB＝AC＝10，AN＝5 ， ∴MN 最大＝2 +5 ＝7 ， ∴S△PMN 最大＝ PM2＝ × MN2＝ ×（7 ）2＝ ． 方法 2：由（2）知，△PMN 是等腰直角三角形，PM＝PN＝ BD， ∴PM 最大时，△PMN 面积最大， ∴点 D 在 BA 的延长线上， ∴BD＝AB+AD＝14， ∴PM＝7， ∴S△PMN 最大＝ PM2＝ ×72＝ ． 【点评】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和 性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出 PM＝ CE，PN＝ BD，解（2）的关键是判断出△ABD≌△ACE，解（3）的关键是判断出 MN 最大 时，△PMN 的面积最大． 23．【分析】（1）由 A、B 两点的坐标，利用待定系数法即可求得抛物线解析式； （2） ① 连接 CD，则可知 CD∥x 轴，由 A、F 的坐标可知 F、A 到 CD 的距离，利用三角形面积 公式可求得△ACD 和△FCD 的面积，则可求得四边形 ACFD 的面积； ② 由题意可知点 A 处不可 能是直角，则有∠ADQ＝90°或∠AQD＝90°，当∠ADQ＝90°时，可先求得直线 AD 解析式， 则可求出直线 DQ 解析式，联立直线 DQ 和抛物线解析式则可求得 Q 点坐标；当∠AQD＝90°时， 设 Q（t，﹣t2+2t+3），设直线 AQ 的解析式为 y＝k1x+b1，则可用 t 表示出 k′，设直线 DQ 解析 式为 y＝k2x+b2，同理可表示出 k2，由 AQ⊥DQ 则可得到关于 t 的方程，可求得 t 的值，即可求得 Q 点坐标． 【解答】解： （1）由题意可得 ，解得 ， ∴抛物线解析式为 y＝﹣x2+2x+3； （2） ① ∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4， ∴F（1，4）， ∵C（0，3），D（2，3）， ∴CD＝2，且 CD∥x 轴， ∵A（﹣1，0）， ∴S 四边形 ACFD＝S△ACD+S△FCD＝ ×2×3+ ×2×（4﹣3）＝4； ② ∵点 P 在线段 AB 上， ∴∠D AQ 不可能为直角， ∴当△AQD 为直角三角形时，有∠ADQ＝90°或∠AQD＝90°， i．当∠ADQ＝90°时，则 DQ⊥AD， ∵A（﹣1，0），D（2，3）， ∴直线 AD 解析式为 y＝x+1， ∴可设直线 DQ 解析式为 y＝﹣x+b′， 把 D（2，3）代入可求得 b′＝5， ∴直线 DQ 解析式为 y＝﹣x+5， 联立直线 DQ 和抛物线解析式可得 ，解得 或 ， ∴Q（1，4）； ii．当∠AQD＝90°时，设 Q（t，﹣t2+2t+3）， 设直线 AQ 的解析式为 y＝k1x+b1， 把 A、Q 坐标代入可得 ，解得 k1＝﹣（t﹣3）， 设直线 DQ 解析式为 y＝k2x+b2，同理可求得 k2＝﹣t， ∵AQ⊥DQ， ∴k1k2＝﹣1，即 t（t﹣3）＝﹣1，解得 t＝ ， 当 t＝ 时，﹣t2+2t+3＝ ， 当 t＝ 时，﹣t2+2t+3＝ ， ∴Q 点坐标为（ ， ）或（ ， ）； 综上可知 Q 点坐标为（1，4）或（ ， ）或（ ， ）． 【点评】本题为二次函数的综合应用，涉及待定系数法、三角形的面积、二次函数的性质、直角 三角形的性质及 分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2） ① 中注意把四 边形转化为两个三角形，在 ② 利用互相垂直直线的性质是解题的关键．本题考查知识点较多，综 合性较强，难度适中．