- 2021-04-19 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市中考数学模拟试题压轴题分析宝山
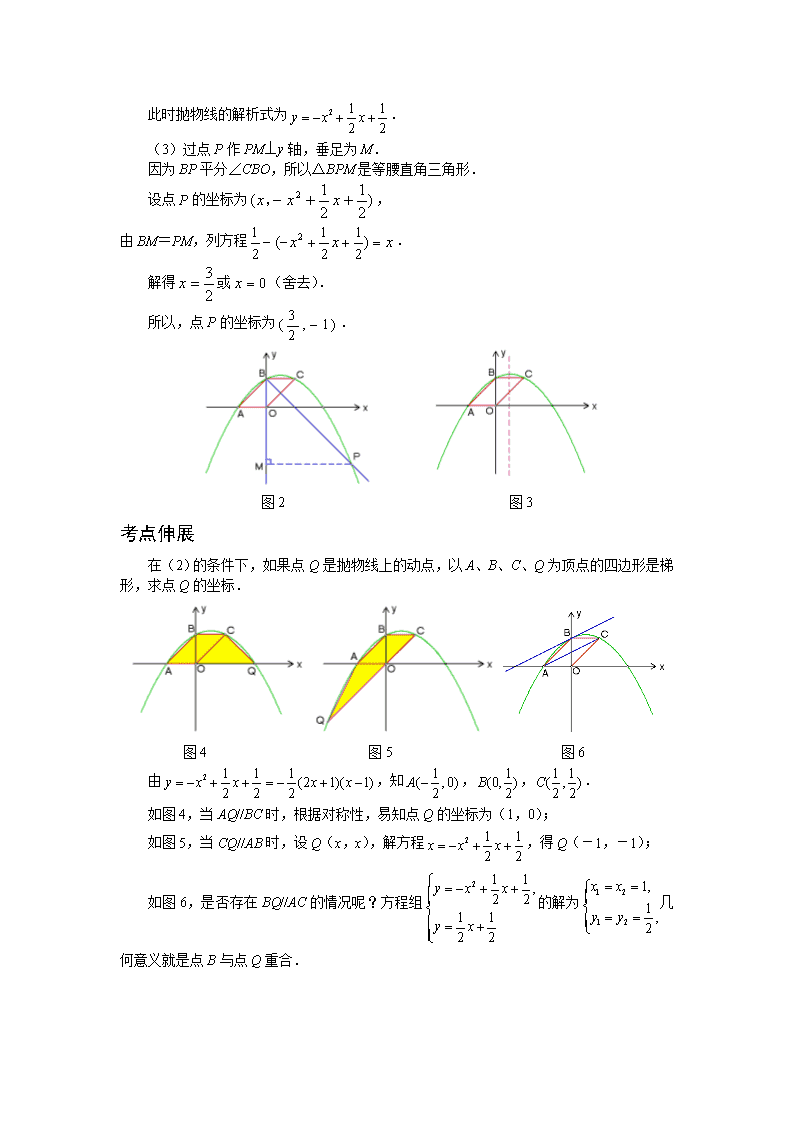
例 2011年上海市宝山区中考模拟第24题 如图1,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB. (1)求b+c的值; (2)若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式; (3)在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标. 图1 动感体验 请打开几何画板文件名“11宝山24”,拖动点B在y轴正半轴上运动,观察b随c变化的跟踪图像,可以体验到,b+c等于定值1;在运动过程中,△AOB保持等腰直角三角形,四边形OABC保持平行四边形.双击按钮“点C落在抛物线上”,可以看到,此时点B与点C关于抛物线的对称轴对称,△BPM是等腰直角三角形. 请打开超级画板文件名“11宝山24”, 思路点拨 1.数形结合,由抛物线的解析式写出点B的坐标,根据OA=OB写出点A的坐标,将点A的坐标代入抛物线的解析式,就可以得到b+c等于定值1. 2.由于△AOB保持等腰直角三角形,当四边形OABC是平行四边形时,点C的坐标可以表示为(c,c). 3.第(3)题中,构造等腰直角三角形BPM,根据BM=PM列方程. 满分解答 (1)因为抛物线y=-x2+bx+c与y轴正半轴交于点B, 所以点B的坐标为(0,c). 因为OA=OB,所以点A的坐标为(-c,0). 将点A(-c,0)代入y=-x2+bx+c,得-c2+bc+c=0. 因为c≠0,整理,得b+c=1. (2)如果四边形OABC是平行四边形,那么BC//AO,BC=AO. 因此点C的坐标可以表示为(c,c). 当点C(c,c)落在抛物线y=-x2+bx+c上时,得-c2+bc+c=c. 整理,得b=c. 结合第(1)题的结论b+c=1,得. 此时抛物线的解析式为. (3)过点P作PM⊥y轴,垂足为M. 因为BP平分∠CBO,所以△BPM是等腰直角三角形. 设点P的坐标为, 由BM=PM,列方程. 解得或(舍去). 所以,点P的坐标为. 图2 图3 考点伸展 在(2)的条件下,如果点Q是抛物线上的动点,以A、B、C、Q为顶点的四边形是梯形,求点Q的坐标. 图4 图5 图6 由,知,,. 如图4,当AQ//BC时,根据对称性,易知点Q的坐标为(1,0); 如图5,当CQ//AB时,设Q(x,x),解方程,得Q(-1,-1); 如图6,是否存在BQ//AC的情况呢?方程组的解为几何意义就是点B与点Q重合.查看更多