高中数学第四章框图4_1流程图课堂探究新人教B版选修1-2

高中数学第四章框图4_1流程图课堂探究新人教B版选修1-2

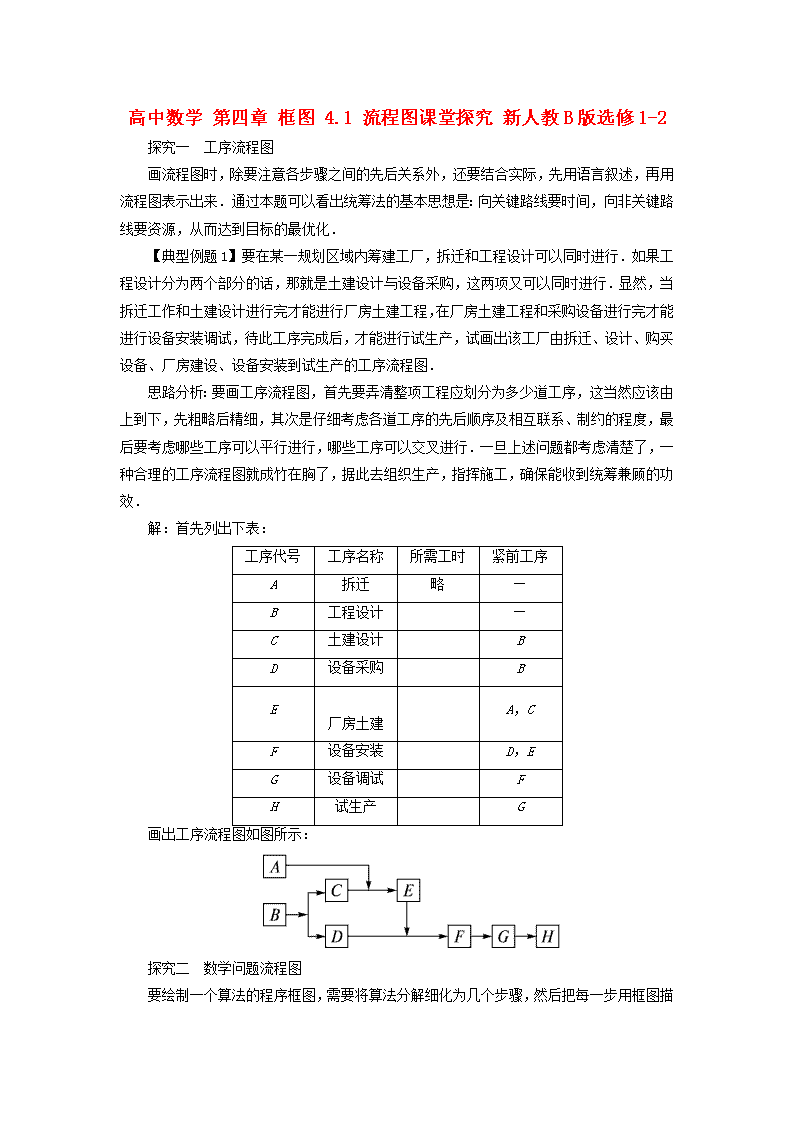
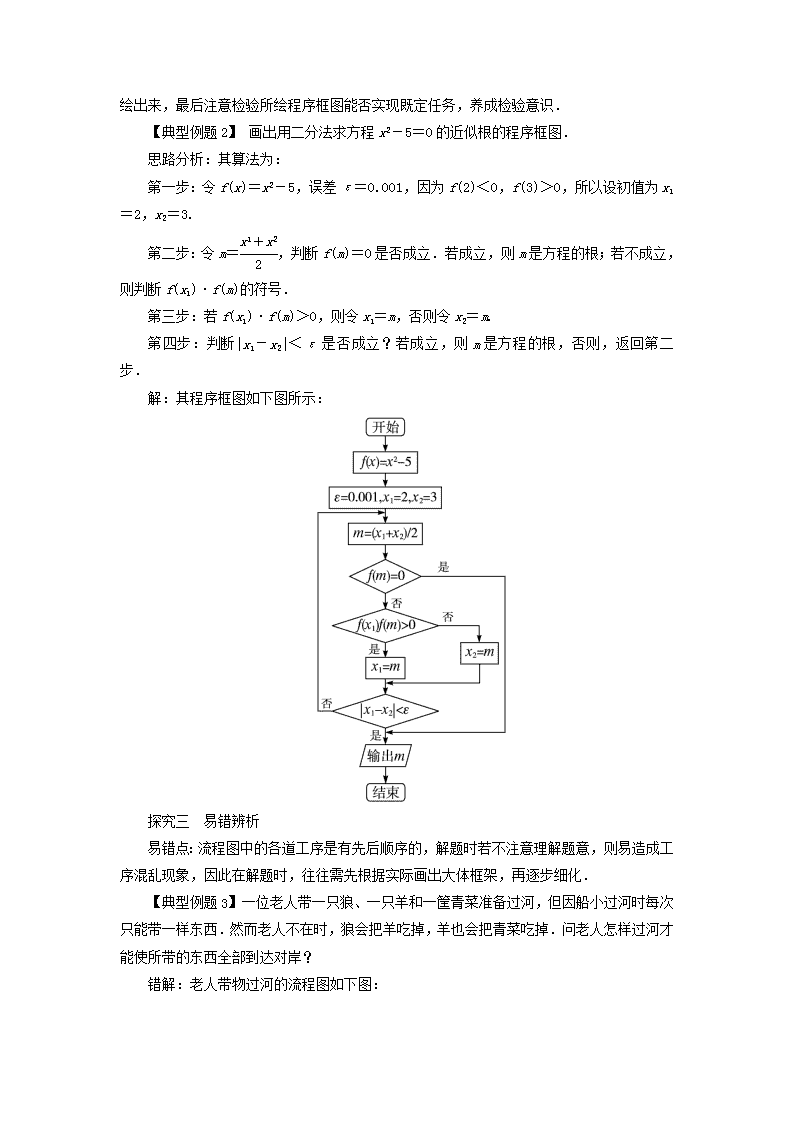
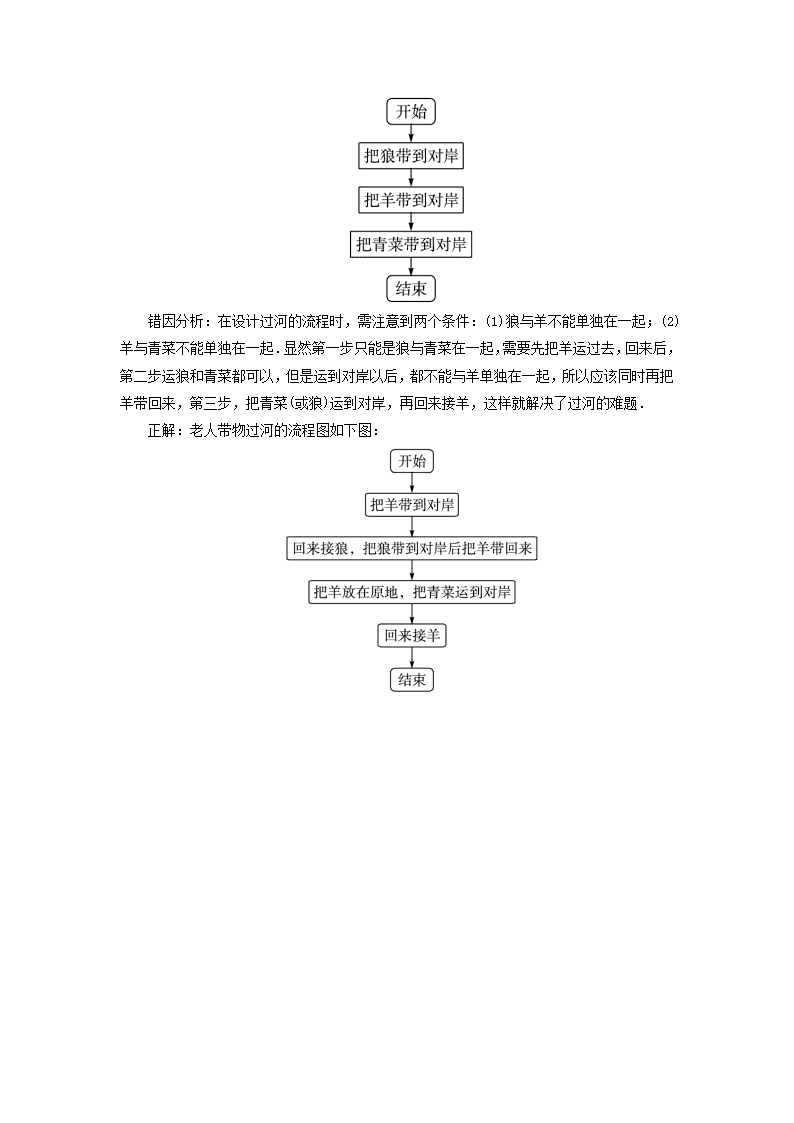
高中数学 第四章 框图 4.1 流程图课堂探究 新人教 B 版选修 1-2 探究一 工序流程图 画流程图时，除要注意各步骤之间的先后关系外，还要结合实际，先用语言叙述，再用 流程图表示出来．通过本题可以看出统筹法的基本思想是：向关键路线要时间，向非关键路 线要资源，从而达到目标的最优化． 【典型例题 1】 要在某一规划区域内筹建工厂，拆迁和工程设计可以同时进行．如果 工程设计分为两个部分的话，那就是土建设计与设备采购，这两项又可以同时进行．显然， 当拆迁工作和土建设计进行完才能进行厂房土建工程，在厂房土建工程和采购设备进行完才 能进行设备安装调试，待此工序完成后，才能进行试生产，试画出该工厂由拆迁、设计、购 买设备、厂房建设、设备安装到试生产的工序流程图． 思路分析：要画工序流程图，首先要弄清整项工程应划分为多少道工序，这当然应该由 上到下，先粗略后精细，其次是仔细考虑各道工序的先后顺序及相互联系、制约的程度，最 后要考虑哪些工序可以平行进行，哪些工序可以交叉进行．一旦上述问题都考虑清楚了，一 种合理的工序流程图就成竹在胸了，据此去组织生产，指挥施工，确保能收到统筹兼顾的功 效． 解：首先列出下表： 工序代号 工序名称 所需工时 紧前工序 A 拆迁 略 — B 工程设计 — C 土建设计 B D 设备采购 B E 厂房土建 A，C F 设备安装 D，E G 设备调试 F H 试生产 G 画出工序流程图如图所示： 探究二 数学问题流程图 要绘制一个算法的程序框图，需要将算法分解细化为几个步骤，然后把每一步用框图描 绘出来，最后注意检验所绘程序框图能否实现既定任务，养成检验意识． 【典型例题 2】 画出用二分法求方程 x2－5＝0 的近似根的程序框图． 思路分析：其算法为： 第一步：令 f(x)＝x2－5，误差ε＝0.001，因为 f(2)＜0，f(3)＞0，所以设初值为 x1 ＝2，x2＝3. 第二步：令 m＝x1＋x2 2 ，判断 f(m)＝0 是否成立．若成立，则 m 是方程的根；若不成立， 则判断 f(x1)·f(m)的符号． 第三步：若 f(x1)·f(m)＞0，则令 x1＝m，否则令 x2＝m. 第四步：判断|x1－x2|＜ε是否成立？若成立，则 m 是方程的根，否则，返回第二步． 解：其程序框图如下图所示： 探究三 易错辨析 易错点：流程图中的各道工序是有先后顺序的，解题时若不注意理解题意，则易造成工 序混乱现象，因此在解题时，往往需先根据实际画出大体框架，再逐步细化． 【典型例题 3】 一位老人带一只狼、一只羊和一筐青菜准备过河，但因船小过河时每 次只能带一样东西．然而老人不在时，狼会把羊吃掉，羊也会把青菜吃掉．问老人怎样过河 才能使所带的东西全部到达对岸？ 错解：老人带物过河的流程图如下图： 错因分析：在设计过河的流程时，需注意到两个条件：(1)狼与羊不能单独在一起；(2) 羊与青菜不能单独在一起．显然第一步只能是狼与青菜在一起，需要先把羊运过去，回来后， 第二步运狼和青菜都可以，但是运到对岸以后，都不能与羊单独在一起，所以应该同时再把 羊带回来，第三步，把青菜(或狼)运到对岸，再回来接羊，这样就解决了过河的难题． 正解：老人带物过河的流程图如下图：