- 2021-04-19 发布 |
- 37.5 KB |
- 11页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学试题分项版解析汇编专题43四边形原卷版
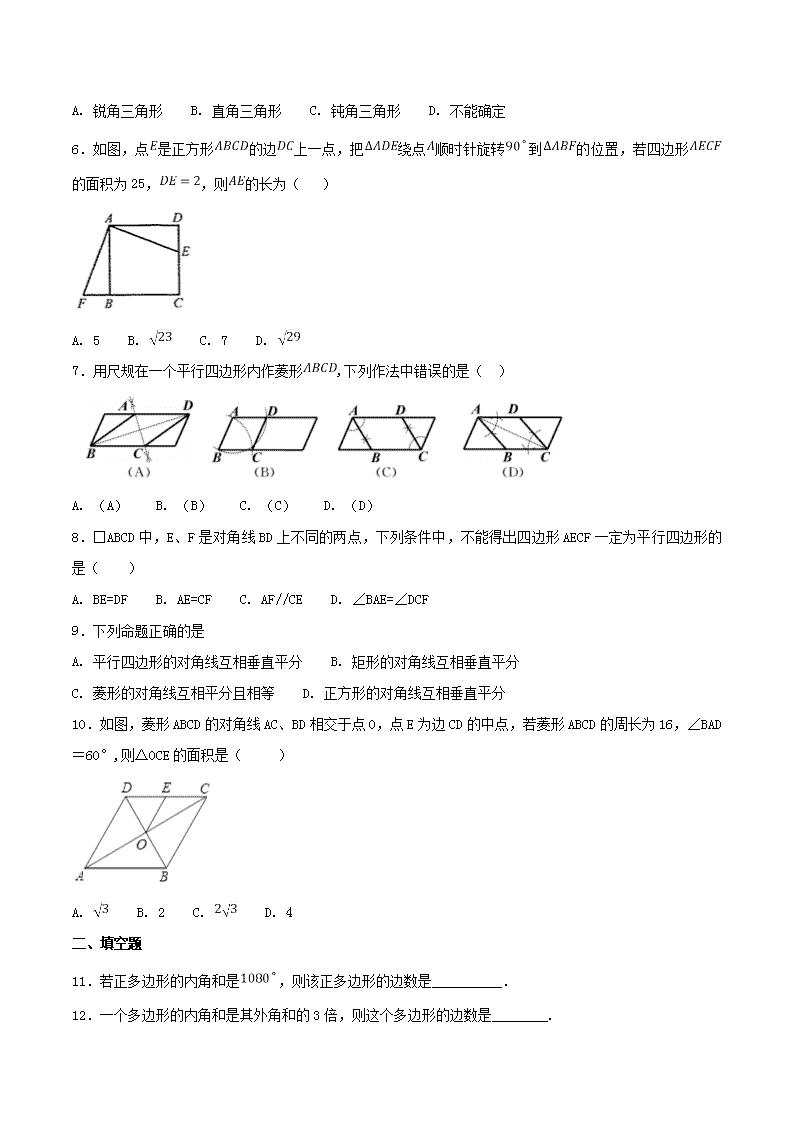
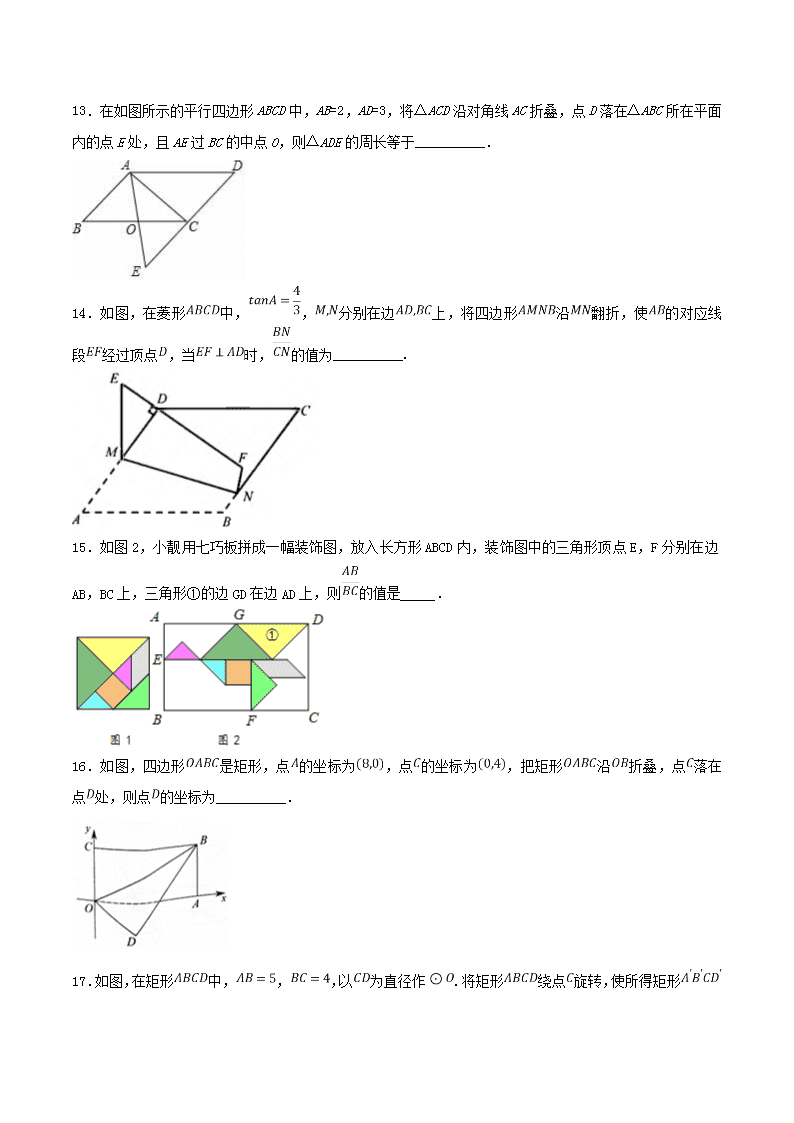
专题4.3 四边形 一、单选题 1.用尺规在一个平行四边形内作菱形,下列作法中错误的是( ) A. B. C. D. 2.如图,菱形的对角线,相交于点,,,则菱形的周长为( ) A. 52 B. 48 C. 40 D. 20 3.如图,将矩形沿对角线折叠,使落在处,交于,则下列结论不一定成立的是( ) A. B. C. D. 4.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是( ) A. B. C. D. 5.在▱ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定 6.如图,点是正方形的边上一点,把绕点顺时针旋转到的位置,若四边形的面积为25,,则的长为( ) A. 5 B. C. 7 D. 7.用尺规在一个平行四边形内作菱形,下列作法中错误的是( ) A. (A) B. (B) C. (C) D. (D) 8.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( ) A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF 9.下列命题正确的是 A. 平行四边形的对角线互相垂直平分 B. 矩形的对角线互相垂直平分 C. 菱形的对角线互相平分且相等 D. 正方形的对角线互相垂直平分 10.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( ) A. B. 2 C. D. 4 二、填空题 11.若正多边形的内角和是,则该正多边形的边数是__________. 12.一个多边形的内角和是其外角和的3倍,则这个多边形的边数是________. 13.在如图所示的平行四边形ABCD中,AB=2,AD=3,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处,且AE过BC的中点O,则△ADE的周长等于__________. 14.如图,在菱形中,,分别在边上,将四边形沿翻折,使的对应线段经过顶点,当时,的值为__________. 15.如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,则的值是_____. 16.如图,四边形是矩形,点的坐标为,点的坐标为,把矩形沿折叠,点落在点处,则点的坐标为__________. 17.如图,在矩形中,,,以为直径作.将矩形绕点旋转,使所得矩形 的边与相切,切点为,边与相交于点,则的长为__________. 18.如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号) ①当E为线段AB中点时,AF∥CE; ②当E为线段AB中点时,AF=; ③当A、F、C三点共线时,AE=; ④当A、F、C三点共线时,△CEF≌△AEF. 19.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE=,∠EAF=45°,则AF的长为_____. 20.如图,在矩形中,,,将矩形沿折叠,点落在处,若的延长线恰好过点,则的值为__________. 三、解答题 21.如图,,,,在一条直线上,已知,,,连接.求证:四边形是平行四边形. 22.小敏思考解决如下问题: 原题:如图1,点,分别在菱形的边,上,,求证:. (1)小敏进行探索,若将点,的位置特殊化:把绕点旋转得到,使,点,分别在边,上,如图2,此时她证明了.请你证明. (2)受以上(1)的启发,在原题中,添加辅助线:如图3,作,,垂足分别为,.请你继续完成原题的证明. (3)如果在原题中添加条件:,,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分). 23.如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF. 24.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根. (1)求证:PA•BD=PB•AE; (2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由. 25.如图,点是正方形边上一点,连接,作于点,手点,连接. (1)求证:; (2已知,四边形的面积为24,求的正弦值. 26.在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示. (1)求证:△ABE≌△ADF; (2)试判断四边形AECF的形状,并说明理由. 27.已知矩形中,是边上的一个动点,点,,分别是,,的中点. (1)求证:; (2)设,当四边形是正方形时,求矩形的面积. 28.如图,在□ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H,求证:AG=CH. 29.如图,在平行四边形中,,点是的中点,连接并延长,交的延长线于点,连接. (1)求证:四边形是菱形; (2)若,,求菱形的面积. 30.如图,在正方形中,是上一点,连接.过点作,垂足为.经过点、、,与相交于点. (1)求证; (2)若正方形的边长为,,求的半径. 31.如图,在四边形中,,.是四边形内一点,且.求证:(1);(2)四边形是菱形. 32.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF. (1)求证:四边形ACDF是平行四边形; (2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由. 33.如图,已知四边形中,对角线相交于点,且,,过点作,分别交于点. (1)求证: ; (2)判断四边形的形状,并说明理由. 34.如图,等边的顶点,在矩形的边,上,且. 求证:矩形是正方形. 35.如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形. 36.在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G. (1)如图,点D在线段CB上,四边形ACDE是正方形. ①若点G为DE中点,求FG的长. ②若DG=GF,求BC的长. (2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由. 37.在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点,,的对应点分别为,,. (Ⅰ)如图①,当点落在边上时,求点的坐标; (Ⅱ)如图②,当点落在线段上时,与交于点. ①求证; ②求点的坐标. (Ⅲ)记为矩形对角线的交点,为的面积,求的取值范围(直接写出结果即可). 38.如图,在平行四边形中,点是对角线的中点,点是上一点,且,连接并延长交于点,过点作的垂线,垂足为,交于点. (1)若,,求的面积; (2)若,求证:. 39.如图,中,是上一点,于点,是的中点,于点,与交于点,若,平分,连接,. (1)求证:; (2)小亮同学经过探究发现:.请你帮助小亮同学证明这一结论. (3)若,判定四边形是否为菱形,并说明理由. 40.阅读短文,解决问题 如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”. 如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB. (1)求证:四边形AEFD是△ABC的“亲密菱形”; (2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积. 41.(题文)(题文)在数学兴趣小组活动中,小亮进行数学探究活动.△ABC是边长为2的等边形,E是AC上一点,小亮以BE为边向BE的右侧作等边三角形BEF,连接CF. (1)如图1,当点E在线段AC上时,EF、BC相交于点D,小亮发现有两个三角形全等,请你找出来,并证明. (2)当点E在线段上运动时,点F也随着运动,若四边形ABFC的面积为,求AE的长. (3)如图2,当点E在AC的延长线上运动时,CF、BE相交于点D,请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系.并说明理由. (4)如图2,当△ECD的面积S1= 时,求AE的长.查看更多