六年级数学下册课件-5 数学广角—鸽巢问题-人教版(共13张PPT)

六年级数学下册课件-5 数学广角—鸽巢问题-人教版(共13张PPT)

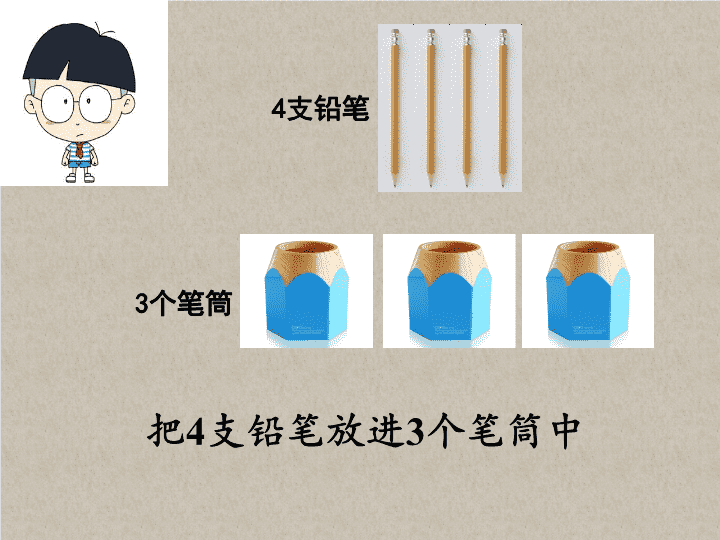
5 数学广角——鸽巢问题 你能写出一个没有重复数字的手机 号码吗？ 4支铅笔 3个笔筒 把4支铅笔放进3个笔筒中 把4支铅笔放入3个笔筒中： ①、可能有一个笔筒中没有铅笔。 ②、可能有一个笔筒中有4支铅笔。 ③、不可能每个笔筒中都有铅笔。 ④、不管怎么放，总有一个笔筒中至少有2支铅笔。 以上结论中， 哪些是正确的？ 把4支铅笔放入3个笔筒中，不管怎么放， 总有一个笔筒中至少有2支铅笔？ 操作要求： 1、小组分工合作，用学具摆一摆并记录下来，或者 直接在纸上画图。 2、找出所有的摆法，注意做到不重复，不遗漏。 把4支铅笔放入3个笔筒中，不管怎么放， 总有一个笔筒中至少有2支铅笔 ？。 （4, 0, 0） （3, 1, 0） （2, 2, 0） （2, 1, 1） （4, 0, 0） （3, 1, 0） （2, 2, 0） （2, 1, 1） 只要摆出一种情况，就能证明 这个结论是正确的！ 把4支铅笔放入3个笔筒中，不管怎么放， 总有一个笔筒中至少有2支铅笔。 5支铅笔放进4个笔筒，不管怎么放， 总有一个笔筒中至少有2支铅笔。 6支铅笔放进5个笔筒，不管怎么放， 总有一个笔筒中至少有 支铅笔。2 2 7支铅笔放进6个笔筒，不管怎么放， 总有一个笔筒中至少有 支铅笔。 …… 5支铅笔放进3个笔筒，不管怎么放， 总有一个笔筒中至少有 支铅笔。2 2 3 6支铅笔放进3个笔筒，不管怎么放， 总有一个笔筒中至少有 支铅笔。 7支铅笔放进3个笔筒，不管怎么放， 总有一个笔筒中至少有 支铅笔。 “狄利克雷原理”， 最先是由19世 纪的德国数学家狄利克雷提出来的 又称“抽屉原理”，还叫做 “鸽巢 原理” 。 “鸽巢原理”的应用是 千变万化的，用它可以解决许多有 趣的问题，并且常常能得到一些令 人惊异的结果。 狄利克雷 （1805～1859） 7只鸽子飞进5个鸽笼，总有一个鸽 笼至少飞进了几只鸽子？ 谢 谢