- 2021-04-19 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
文数立体几何高考题训练
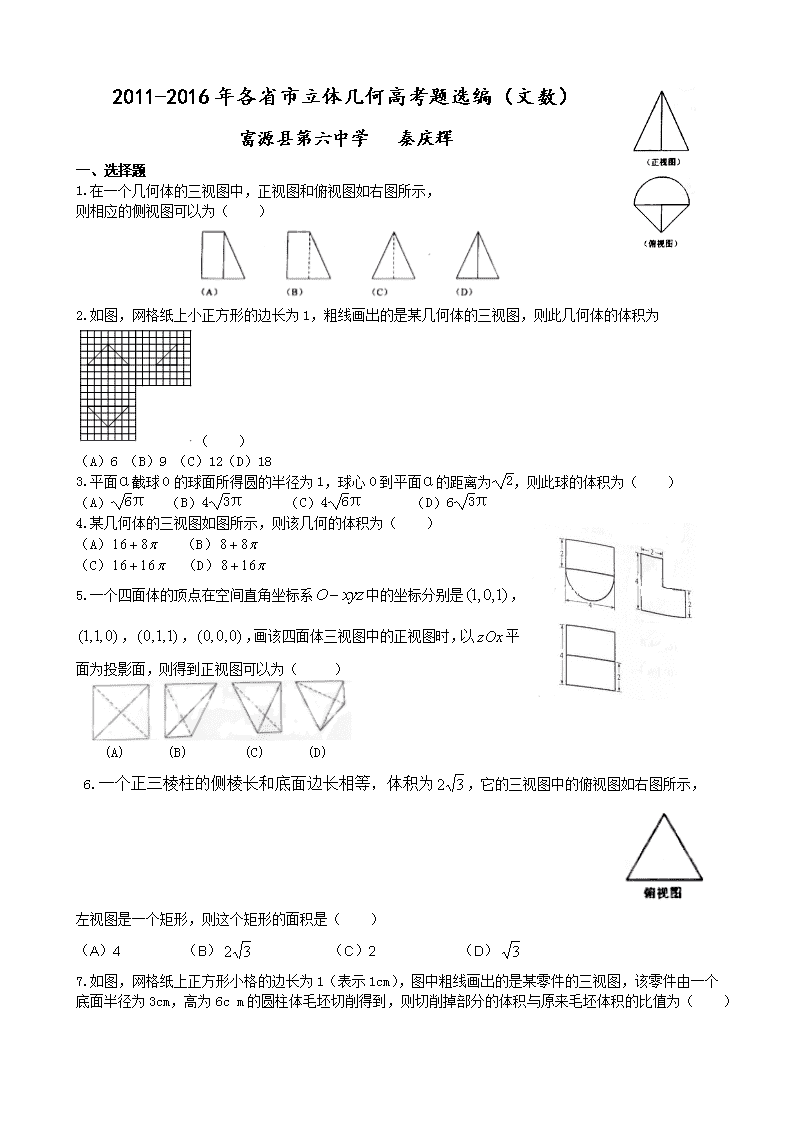
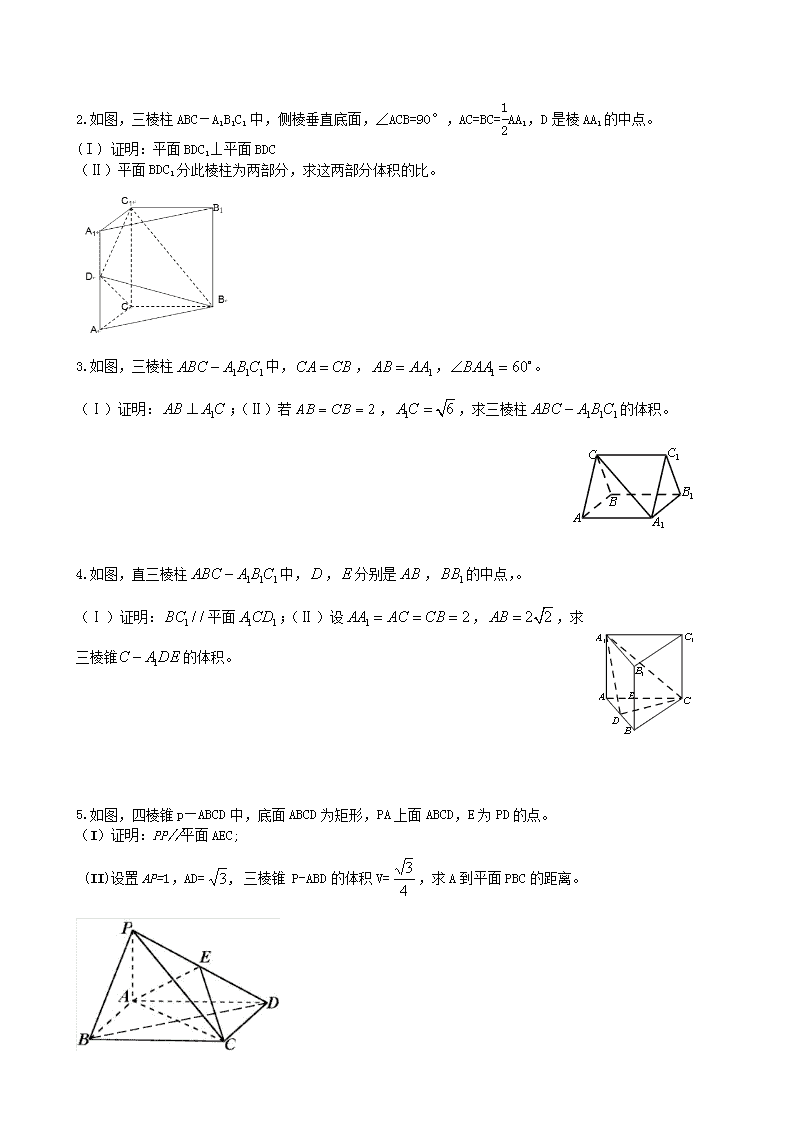
2011-2016年各省市立体几何高考题选编(文数) 富源县第六中学 秦庆辉 一、选择题 1.在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的侧视图可以为( ) 2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 ( ) (A)6 (B)9 (C)12(D)18 3.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( ) (A)π (B)4π (C)4π (D)6π 4.某几何体的三视图如图所示,则该几何的体积为( ) (A) (B) (C) (D) 5.一个四面体的顶点在空间直角坐标系中的坐标分别是,,,,画该四面体三视图中的正视图时,以平面为投影面,则得到正视图可以为( ) (A) (B) (C) (D) 6.一个正三棱柱的侧棱长和底面边长相等,体积为,它的三视图中的俯视图如右图所示, 左视图是一个矩形,则这个矩形的面积是( ) (A)4 (B) (C)2 (D) 7.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6c m的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( ) (A) (B) (C) (D) 8.正三棱柱的底面边长为2,侧棱长为,D为BC中点,则三棱锥的体积为( ) (A)3 (B) (C)1 (D) 9.已知球的直径SC=4, A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( ) (A) (B) (C) (D) 10.已知A,B是球O的球面上两点,∠AOB = 90°,C为该球面上的动点。若三棱锥O—ABC体积的最大值为36,则球O的表面积为( ) A.36π B.64π C.144π D.256π 二、填空题 1.已知两个圆锥有公共底面,且两个圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的 ,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为 。 2.已知是球的直径上一点,,平面,为垂足,截球所得截面的面积为,则球的表面积为_______。 3.已知正四棱锥的体积为,底面边长为,则以为球心,为半径的球的表面积为________。 4.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是_______。 5.在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是 _______。 三、解答题 1.如图,四棱锥中,底面为平行四边形。 底面 。 (I)证明: (II)设,求棱锥的高。 2.如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。 (I) 证明:平面BDC1⊥平面BDC (Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比。 3.如图,三棱柱中,,,。 (Ⅰ)证明:;(Ⅱ)若,,求三棱柱的体积。 4.如图,直三棱柱中,,分别是,的中点,。 (Ⅰ)证明:平面;(Ⅱ)设,,求三棱锥的体积。 5.如图,四棱锥p—ABCD中,底面ABCD为矩形,PA上面ABCD,E为PD的点。 (I)证明:PP//平面AEC; (II)设置AP=1,AD=, 三棱锥 P-ABD的体积V=,求A到平面PBC的距离。 6.如图,长方体ABCD—A1B1C1D1中,AB = 16,BC = 10,AA1 = 8,点E,F分别在A1B1,D1C1上,A1E = D1F = 4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形。 (I)在图中画出这个正方形(不必说明画法和理由); (II)求平面α把该长方体分成的两部分体积的比值。 7. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD。 (I)证明:PQ⊥平面DCQ; (II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。 8.如图,在四棱锥中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点 (I)证明:直线EF‖平面PCD;(II)证明:平面BEF⊥平面PAD 9. 如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, . (Ⅰ) 证明: A1BD // 平面CD1B1; (Ⅱ) 求三棱柱ABD-A1B1D1的体积. 查看更多