初中数学中考复习课件章节考点专题突破：第六章 图形性质2-27 几何作图

初中数学中考复习课件章节考点专题突破：第六章 图形性质2-27 几何作图

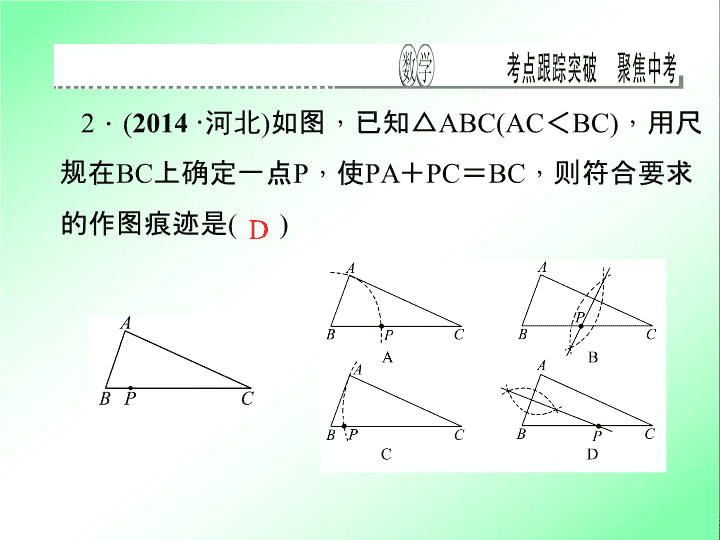
考点跟踪突破 27 　几何作图 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 滨州 ) 如图， 是我们学过的用直尺和三角尺画平行线的方法示意图 ， 画图的原理是 ( ) A ． 同位角相等 ， 两直线平行 B ． 内错角相等 ， 两直线平行 C ． 两直线平行 ， 同位角相等 D ． 两直线平行 ， 内错角相等 A 2 ． ( 2014 · 河北 ) 如图 ， 已知 △ ABC(AC ＜ BC) ， 用尺规在 BC 上确定一点 P ， 使 PA ＋ PC ＝ BC ， 则符合要求的作图痕迹是 ( ) D 3 ． ( 2013· 咸宁 ) 如图 ， 在平面直角坐标系中 ， 以点 O 为圆 心 ， 适当长为半径画弧 ， 交 x 轴于点 M ， 交 y 轴于点 N ， 再分别以点 M ， N 为圆心 ， 大于 1 2 MN 的长为半径画弧 ， 两弧在第二象限交于点 P. 若点 P 的坐标为 (2a ， b ＋ 1) ， 则 a 与 b 的数量关系为 ( ) A ． a ＝ b B ． 2a ＋ b ＝－ 1 C ． 2a － b ＝ 1 D ． 2a ＋ b ＝ 1 B 4 ． ( 2013· 河北 ) 如图 ， 线段 AB ， BC ， ∠ ABC ＝ 90 ° ， 求作矩 形 ABCD. 以下是甲、乙两同学 的作业： 甲： 1. 以点 C 为圆心 ， AB 长 为半径画弧； 2 ． 以点 A 为圆心 ， BC 长为半径画弧； 3 ． 两弧在 BC 上方交于点 D ， 连接 AD ， CD ， 四边形 ABCD 即为所求 ( 如图 ① ) ． 乙： 1. 连接 AC ， 作线段 AC 的垂直平分线 ， 交 AC 于点 M ； 2. 连接 BM 并延长 ， 在延长线上取一点 D ， 使 MD ＝ MB ， 连接 AD ， CD ， 四边形 ABCD 即为所求 ( 如 图 ② ) ． 对于两人的作业 ， 下列说法正确的是 ( ) A ． 两人都对 B ．两人都不对 C ． 甲对、乙不对 D ．甲不对、乙对 A 5 ． ( 2013· 遂宁 ) 如图 ， 在 △ ABC 中 ， ∠ C ＝ 90 ° ， ∠ B ＝ 30 ° ， 以 A 为圆心 ， 任意长为半径画弧分别交 AB ， AC 于点 M 和 N ， 再分别以 M ， N 为圆心 ， 大于 1 2 MN 的长为半径画弧 ， 两弧交于点 P ， 连接 AP 并延长交 BC 于点 D ， 则下列说法中正确的个数是 ( ) ① AD 是 ∠ BAC 的平分线； ②∠ ADC ＝ 60 ° ； ③ 点 D 在 AB 的垂直 平分线上； ④ S △ DAC ∶ S △ ABC ＝ 1 ∶ 3. A ． 1 B ． 2 C ． 3 D ． 4 D 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014· 河南 ) 在 △ ABC 中 ， 按以下步骤作图： ① 分别以 B ， C 为圆心 ， 以大于 1 2 BC 的长为半径作弧 ， 两弧相交于 两点 M ， N ； ② 作直线 MN 交 AB 于点 D ， 连接 CD. 若 CD ＝ AC ， ∠ B ＝ 25 ° ， 则 ∠ ACB 的度数为 __ __ ． 105° 7 ． ( 2014· 梅州 ) 如图 ， 在 Rt △ ABC 中 ， ∠ B ＝ 90 ° ， 分别 以 A ， C 为圆心 ， 大于 1 2 AC 长为半径画弧 ， 两弧相交于点 M ， N ， 连接 MN ， 与 AC ， BC 分别交于点 D ， E ， 连接 AE ， 则： (1) ∠ ADE ＝ __ __ ； (2)AE__ __EC ； ( 填 “ ＞ ”“ ＜ ” 或 “ ＝ ” ) (3) 当 AB ＝ 3 ， AC ＝ 5 时 ， △ ABE 的周长＝ __ __ ． 90° ＝ 7 8 ． 数学活动课上 ， 老师在黑板上画直线平行于射线 AN( 如图 ) ， 让同学们在直线 l 和射线 AN 上各找一点 B 和 C ， 使得以 A ， B ， C 为顶点的三角形是等腰直角三角形．这样的三角形最多能画 ____ 个． 3 9 ．如图 ， 以点 O 为圆心 ， 任意长为半径画弧 ， 与射线 OM 交于点 A ， 再以点 A 为圆心 ， AO 长为半径画弧 ， 两弧交于点 B ， 画射线 OB ， 则 cos ∠ AOB 的值等于 ____ ． 10 ． 如图所示 ， 已知线段 a ， c 和 ∠ α ， 求作： △ ABC ， 使 BC ＝ a ， AB ＝ c ， ∠ ABC ＝ ∠ α ， 根据作图把下面空格填上适当的文字或字母． (1) 如图 ① 所示 ， 作 ∠ MBN ＝ ____ ； (2) 如图 ② 所示 ， 在射线 BM 上截取 BC ＝ ____ ， 在射线 BN 上截取 BA ＝ ____ ； (3) 连接 AC ， 如图 ③ 所示 ， △ ABC 就是 ． ∠ α a c 所求作的三角形 三、解答题 ( 共 40 分 ) 11 ． (12 分 ) ( 2013 · 青岛 ) 如图 ， 直线 AB 与直线 BC 相交于点 B ， 点 D 是直线 BC 上一点． 求作：点 E ， 使直线 DE ∥ AB ， 且点 E 到 B ， D 两点的距离相等． ( 在题目的原图中完成作图 ) 解：因为点 E 到 B ， D 两点的距离相等 ， 所以 ， 点 E 一定在线段 BD 的垂直平分线上 ， 首先以点 D 为顶点 ， DC 为边作一个角等于 ∠ ABC ， 再作出 DB 的垂直平分线 ， 即可找到点 E. 如图所示 ， 点 E 即为所求 ， BE ＝ DE 12 ． (14 分 ( 2014 · 孝感 ) 如图 ， 在 Rt △ ABC 中 ， ∠ ACB ＝ 90°. (1) 先作 ∠ ABC 的平分线交 AC 边于点 O ， 再以点 O 为圆心 ， OC 为半径作 ⊙ O ； ( 要求：尺规作图 ， 保留作图痕迹 ， 不写作法 ) (2) 请你判断 (1) 中 AB 与 ⊙ O 的位置关系 ， 并证明你的结论． 解： (1) 如图 ① (2)AB 与 ⊙ O 相切．证明：作 OD ⊥ AB 于点 D ， 如图 ② . ∵ BO 平分 ∠ ABC ， ∠ ACB ＝ 90° ， OD ⊥ AB ， ∴ OD ＝ OC ， ∴ AB 与 ⊙ O 相切 13 ． (14 分 ) ( 2014 · 宁夏 ) 如图 ， △ ABC 中 ， ∠ C ＝ 90° ， ∠ A ＝ 30°. (1) 用尺规作图作 AB 边上的垂直平分线 DE ， 交 AC 于点 D ， 交 AB 于点 E ； ( 保留作图痕迹 ， 不要求写作法和证明 ) (2) 连接 BD ， 求证： BD 平分 ∠ CBA. 解： (1) 解：如图所示 ， DE 就是要求作的 AB 边上的垂直平分线 (2) 证明： ∵ DE 是 AB 边上的垂直平分线 ， ∠ A ＝ 30° ， ∴ AD ＝ BD ， ∴∠ ABD ＝ ∠ A ＝ 30° ， ∵∠ C ＝ 90° ， ∴∠ ABC ＝ 90° － ∠ A ＝ 90° － 30° ＝ 60° ， ∴∠ CBD ＝ ∠ ABC － ∠ ABD ＝ 60° － 30° ＝ 30° ， ∴∠ ABD ＝ ∠ CBD ， ∴ BD 平分 ∠ CBA