- 2021-04-19 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
黑龙江省实验中学2021届高三8月份阶段测试数学(理)试题 Word版含答案
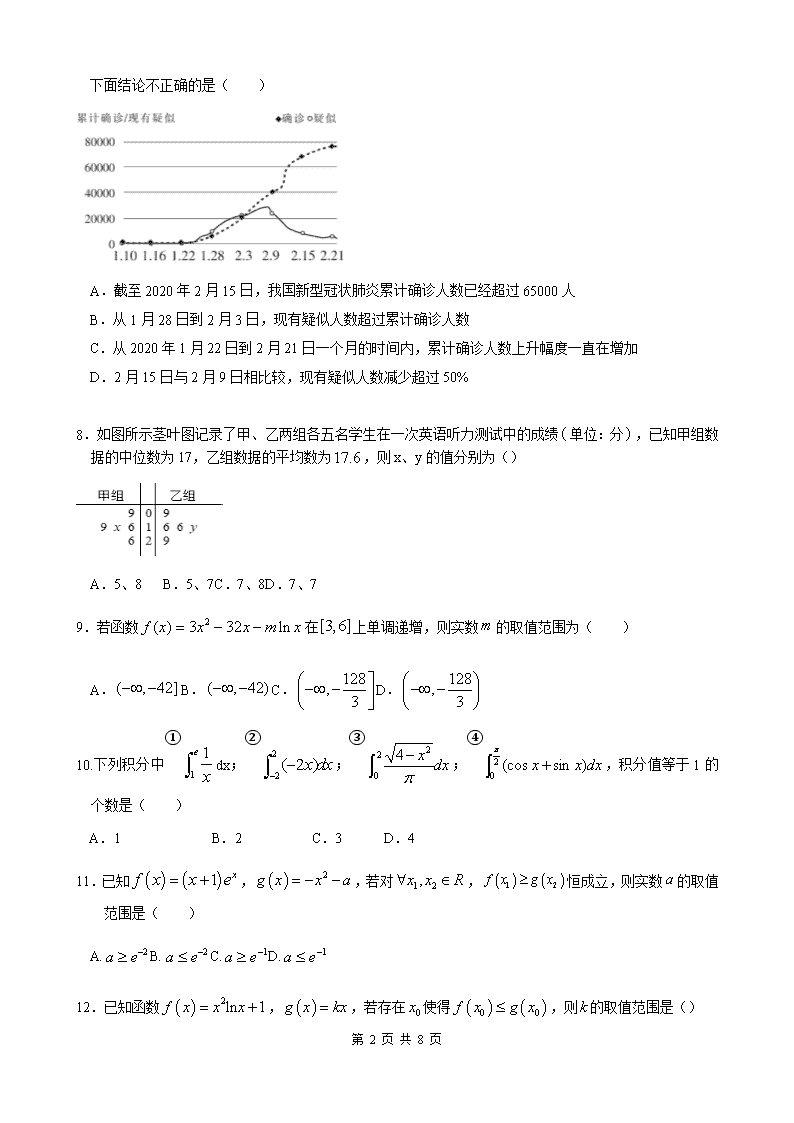
黑龙江省实验中学2020--2021学年度上学期高三8月份阶段测试 数学学科试题(理) 考试时间120分钟 总分150分 一、选择题(本大题共12小题,每小题5分,共60分) 1.某校高一年级有1200名学生,高二年级有1000名学生,高三年级有800名学生,现要从该校全体学生中抽取300人进行视力检查,应从高三年级抽取( )人 A.60B.80C.100D.120 2. 已知集合, ,则( ) A. B. C.D. 或 3.下列函数中,其定义域和值域与函数的定义域和值域相同的是( ) A. B. C. D. 4.条件,且是的充分不必要条件,则可以是( ) A. B. C. D. 5.下列说法正确的是( ) A. 命题:“若”的否命题为假命题; B. 命题“存在,使”的否定为“对任意,都有”; C. 若p且q为假命题,则p、q均为假命题; D. 命题“”是真命题. 6.已知,则等于() A. B. C. D. 7 第 7 页 共 8 页 .已知下图为2020年1月10日到2月21日我国新型冠状肺炎累计确诊人数及现有疑似人数趋势图,则下面结论不正确的是( ) A.截至2020年2月15日,我国新型冠状肺炎累计确诊人数已经超过65000人 B.从1月28日到2月3日,现有疑似人数超过累计确诊人数 C.从2020年1月22日到2月21日一个月的时间内,累计确诊人数上升幅度一直在增加 D.2月15日与2月9日相比较,现有疑似人数减少超过50% 8.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩单位:分,已知甲组数据的中位数为17,乙组数据的平均数为,则x、y的值分别为() A.5、8 B.5、7C.7、8D.7、7 9.若函数在上单调递增,则实数的取值范围为( ) A.B.C.D. 10.下列积分中①dx;②;③;④,积分值等于1的个数是( ) A.1 B.2 C.3 D.4 11.已知,,若对,恒成立,则实数的取值范围是( ) A.B.C.D. 12.已知函数,,若存在使得,则的取值范围是() 第 7 页 共 8 页 A. B. C. D. 二、填空题(本大题共4小题,每小题5分,共20分) 13.已知函数的定义域为,则函数的定义域为. 14.已知函数,则曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积. 15.在哈市高二的联考中,这些学生的数学成绩服从正态分布,随机抽取位学生的成绩,记表示抽取的位学生成绩在之外的人数,则________,的数学期望________. 附:若随机变量服从正态分布,则,,取,. 16.已知函数,若有3个极值点,则实数的取值范围是______. 三、解答题(本大题共6小题,共70分) 17.(满分10分)已知函数. (1)若函数的一条切线方程为,求的值; (2)求证:. 18.(满分12分)考试结束以后,学校对甲、乙两个班的数学考试成绩进行分析,规定:大于或等于80分为优秀,80分以下为非优秀.统计成绩后,得到如下的列联表,且已知在甲、乙两个班全部110人中随机抽取1人为优秀的概率为. (1)完成列联表,并判断是否有99%的把握认为“成绩与班级有关系”; (2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到7号或8号的概率. 第 7 页 共 8 页 优秀 非优秀 合计 甲班 乙班 合计 参考公式与临界值表:. 19.(满分12分)对某校高三年级学生参加社区服务次数进行统计,随机抽取名学生作为样本,得到这名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下: 分组 频数 频率 15 0.30 30 2 合计 1 (1)求出表中,及图中的值; (2)若该校高三学生人数有500人,试估计该校高三学生参加社区服务的次数在区间内的人数; (3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求其中参加社区服务次数在区间内的人数X的分布列及数学期望. 20.(满分12分)“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 第 7 页 共 8 页 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用(单位:万元)和利润(单位:十万元)之间的关系,得到下列数据: 3 4 5 6 7 9 10 12 2 3 4 4 5 6 7 9 (1)请用相关系数说明与之间是否存在线性相关关系(当时,说明与之间具有线性相关关系,结果精确到0.01); (2)根据(1)的判断结果,建立与之间的回归方程,并预测当时,对应的利润为多少(精确到0.01). 附参考公式:回归方程中中和最小二乘估计分别为 ,相关系数 参考数据: . 21.(满分12分)已知, 是的导函数. (1)求的极值; (2)若在时恒成立,求实数的取值范围. 22.(满分12分)已知函数. 第 7 页 共 8 页 (1)讨论的单调性; (2)若恒成立,求实数的最大值. 理科数学试卷答案 一、选择题 1——6 BACADC 7——12 CCABAB 二、填空题 13.[0,3] 14. 15., 16. 三、解答题 17.(1)a=-1;(2)设, 在上增,在上减,,. 18.(1) 优秀 非优秀 合计 甲班 40 50 乙班 30 60 第 7 页 共 8 页 合计 40 70 ,所以,有99%的把握认为“成绩与班级有关系 (2)设“抽到7号或8号”为事件A. 19.(1)M=50, p=0.06 , a=0.12 (2)150 (3)X可能取值0,1,2 x 0 1 2 p 3/10 3/5 1/10 E(X)=4/5 20.(1), (2) 21.解析:(1) , , , 当时, 恒成立, 无极值; 当时, ,即, 由,得;由,得, 所以当时,有极小值. (2),即,即, 令,则, 当时,由知,∴,原不等式成立, 当时, ,即, ,得; ,得, 所以在上单调递减, 又∵,∴不合题意, 第 7 页 共 8 页 综上, 的取值范围为. 22.(1)定义域 ①当时,,∴在上单调递减; ②当,由解得,∴的单调递增区间为, 单调递减区间是和; ③当,同理可得的单调递增区间为,单调递减区间是和. (2)∵恒成立,∴恒成立, 即恒成立, , ∴在上递增,上递减,∴, ∴,∴, 令, ∴在上递增,上递减, ∴,∴,∴实数的最大值为. 第 7 页 共 8 页查看更多