- 2021-04-19 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010中考数学莆田考试试题
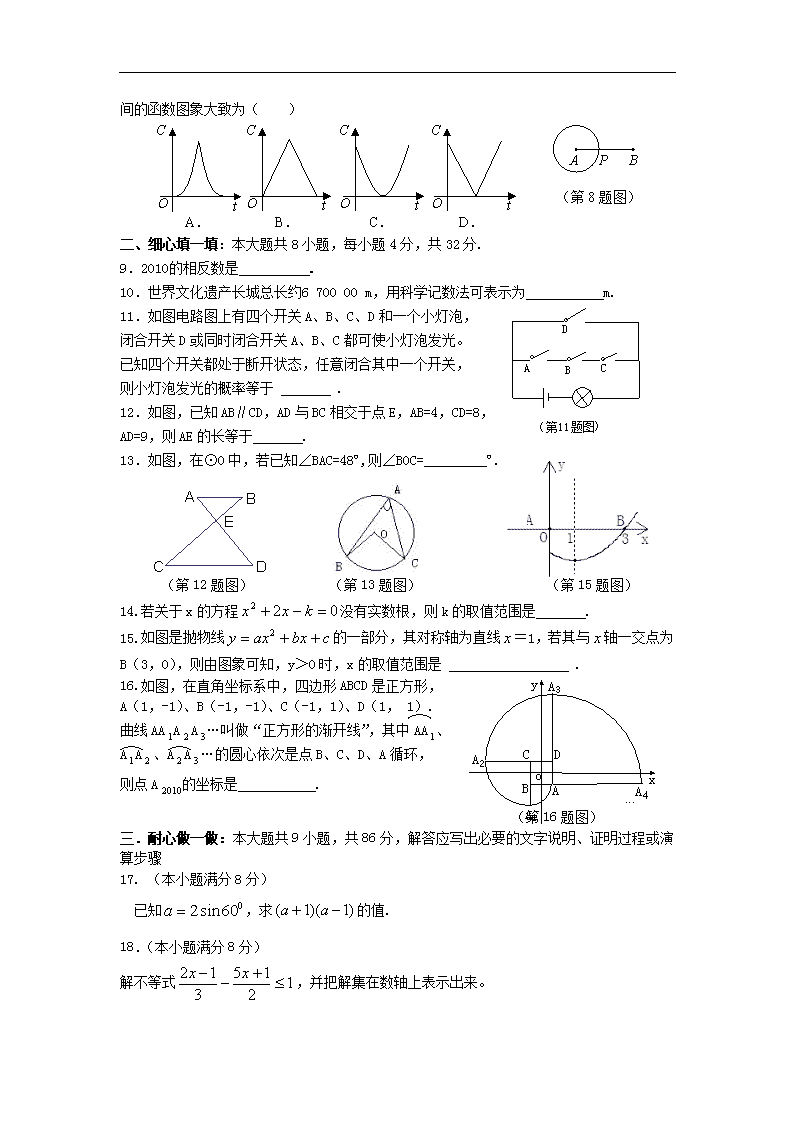
2010年福建省莆田市初中毕业班质量检查试卷 数 学 (满分:150分;考试时间:120分钟) 友情提醒:本试卷分为“试题”和“答题卡”两部分,答题时,请按答题卡中的“注意事项”认真作答,答案写在答题卡上的相应位置。 一、精心选一选:本大题共8小题,每小题4分,共32分,每小题给出的四个选项中有且只有一个选项是正确的, 请把正确选项的代号写在题后的括号内,答对的得4分;答错、不答或答案超过一个的一律得0分. 1.下列运算正确的是( ) A. B. C. D. 2.方程的解是( ) A. B. C.或 D.或 3.某鞋店试销一种新款女鞋,销售情况如下表所示: 型号 22 22.5 23 23.5 24 24.5 25 数量(双) 3 5 10 15 8 3 2 鞋店经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( ) A.平均数 B.众数 C.中位数 D.方差 4.如图,把直线L沿x轴正方向向右平移2个单位得到 直线L′,则直线L/的解析式为( ) A. B. C. D. 5.下列说法正确的是( ) A.有两个角为直角的四边形是矩形 B.矩形的对角线互相垂直 C.等腰梯形的对角线相等 (第4题图) D.对角线互相垂直的四边形是菱形 6.如图,为一个圆锥的三视图,则此圆锥的侧面积是( ) 7.以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( ) A.不能构成三角形 B.这个三角形是等腰三角形 C.这个三角形是直角三角形 D.这个三角形是钝角三角形 8.如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长为半径的圆的周长c与点P的运动时间t 之间的函数图象大致为( ) O C t O C t O C t O C t A P B A. B. C. D. (第8题图) 二、细心填一填:本大题共8小题,每小题4分,共32分. 9.2010的相反数是 . 10.世界文化遗产长城总长约6 700 00 m,用科学记数法可表示为 m. 11.如图电路图上有四个开关A、B、C、D和一个小灯泡, 闭合开关D或同时闭合开关A、B、C都可使小灯泡发光。 已知四个开关都处于断开状态,任意闭合其中一个开关, 则小灯泡发光的概率等于 . 12.如图,已知AB∥CD,AD与BC相交于点E,AB=4,CD=8, AD=9,则AE的长等于 . 13.如图,在⊙O中,若已知∠BAC=48º,则∠BOC=_________º. (第12题图) (第13题图) (第15题图) 14.若关于x的方程没有实数根,则k的取值范围是 . 15.如图是抛物线的一部分,其对称轴为直线=1,若其与轴一交点为B(3,0),则由图象可知,y>0时,x的取值范围是 . 16.如图,在直角坐标系中,四边形ABCD是正方形, A(1,-1)、B(-1,-1)、C(-1,1)、D(1, 1). 曲线AAAA…叫做“正方形的渐开线”,其中AA、 AA、AA…的圆心依次是点B、C、D、A循环, 则点A的坐标是 . (第16题图) 三.耐心做一做:本大题共9小题,共86分,解答应写出必要的文字说明、证明过程或演算步骤 17. (本小题满分8分) 已知,求的值. 18.(本小题满分8分) 解不等式,并把解集在数轴上表示出来。 O D C A B E F 19.(本小题满分8分) 如图,线段与相交于点,E、F分别为OB、 OC的中点,连接AB、DC、EF分别将“” 记为①,“”记为②,“” 记为③, 要求同学从这三个等式中选出两个作为条件, 一个作为结论.(在横线上填上序号) (第19题图) (1) 写出一个真命题: 如果 、 ,那么 .并证明这个真命题. (2) 写出一个假命题:如果 、 ,那么 . 20. (本小题满分8分) 为了提高农民抵御大病风险的能力,全国农村推行了新型农村合作医疗政策,农民只需每人每年交10钱,就可以加入合作医疗,若农民患病住院治疗,出院后可到新型农村合作医疗办公室按一定比例报销医疗费.小军与同学随机调查了他们镇的一些村民,根据收集的数据制成如图所示的统计图。 根据以上信息,解答下列问题: (1)本次共调查多少村民?有多少人参加合作医疗并的到报销款? (2)若该镇有村民10000人,请你估计大约有多少人参加了合作医疗保险?要使两年后参加合作医疗保险的人数达到9680人,假设这两年的增长率相同,求这个年增长率. 21.(本小题满分8分) (1)如图1,D是△ABC的边BC上的一点,且,若△ABD的面积为,△ABC的面积为S,则: S = ; (2)利用图1的结论在图2、3中将△ABC分别按以下两种方式分为三个面积相等的三角形,并说明分点所在的位置. 22.(本小题满分10分) 如图,以菱形ABCD的边AB为直径的⊙O交对角线 AC于点P,过P作PE⊥BC,垂足为E。 ⑴求证:PE是⊙O的切线。 ⑵若菱形ABCD的面积为24,tan,求PE的长. 23.(本小题满分10分) 某水产品养殖企业为指导该企业某种水产品的养殖 和销售,对历年市场行情和水产品养殖情况进行了 调查.调查发现这种水产品的每千克售价y(元) 与销售月份x(月)满足关系式, 而其每千克成本y(元)与销售月份x(月)满足 的函数关系,其图象如图所示. (1)求y的解析式; (2)问这种水产品下半年几月份出售每千克的利润最大?最大利润是多少? 24.(本小题满分12分) 某课题组在探究“泵站问题”时抽象出数学模型: 直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A,连接AB,则AB与直线l的交点即为P,且PA+PB的最小值为AB. 请利用上述模型解决下列问题: (1)几何应用:如图1,等腰直角三角形ABC的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为 ; (2)几何拓展:如图2, △ABC中,AB=2,∠BAC=30,若在AC、AB上各取一点M、N使BM+MN的值最小,求这个最小值; (3)代数应用:求代数式(0≤x≤4)的最小值. 25.如图,矩形ABCD (点A在第一象限)与x轴的正半轴相交于M,,与y的负半轴相交于N, AB∥x轴,反比例函数y=的图象过A、C两点,直线AC与x轴相交于点E、与y轴相交于点F。 (1)若B(-3,3),直线AC的解析式为y=. ①求a的值; ②连结OA、OC,若△OAC的面积记为S,△ABC的面积记为S,记S= S-S,问S是否存在最小值?若存在,求出其最小值;若不存在,请说明理由 (2)AE与CF是否相等?请证明你的结论。 (第25题图) 2010年莆田市初中毕业班数学质量检查试卷参考答案 一、精心选一选: 1. D 2.D 3.B 4.C 5.C 6.B 7.C 8.B 二、细心填一填: 9. -2010 10. 6.7 11. 12. 3 13. 14.k<-1 15. x<-1或x>3 16.(-4021,1) 三.耐心做一做: 17. 解: ∵2sin60 ∴(a+1)(a-1)=a=2 18. 解:原不等式可化为2(2x-1)-3(5x+1)≤6 4x-2-15x-3≤6 -11x≤11 x≥-1 19.(1)①②→③ 或①③→② 证明:∵∠OEF=∠OFE 证明:∵∠A=∠D,AB=DC,∠AOB=∠DOC ∴OE=OF ∴△OAB≌△ODC ∵E、F分别为OB、OC的中点 ∴OB=OC ∴OB=OC ∵E、F分别为OB、OC的中点 在△OAB与△ODC中 ∴OE=OF ∵∠A=∠D,∠AOB=∠DOC,OB=OC ∴∠OEF=∠OFE ∴△OAB≌△ODC ∴AB=DC (2)②③→① 20.答: (1)本次共调查500名村民 被调查的村民中有400×5%=20人参加合作医疗并的到报销款 (2)10000×(人) 设这个增长率为x。依题意得 解得:, (不合题意舍去) 答:该镇大约有8000人参加了合作医疗保险,这个年增长率为10%。 21.(1): S = (2) 22.(1)证明:连接OP、BP. ∵四边形ABCD是菱形 ∴AB=BC ∵AB是直径 ∴∠APB=90 ∴AP=PC 又∵AO=OB ∴OP∥BC ∵PE⊥BC ∴PE⊥OP 所以PE是⊙O的切线. (2) ∵= ∴ 设PB=3x,则PA=4x S ∴x=1 PA=PC=4,PB=3 ∴AB=BC=5 在Rt△BPC中, 23.解(1)依题意得: 解得 (2)设这种水产品每千克的利润为y,则 ∵当x>4时,y随着X的增大而减小。 x的取值范围是:7≤x≤12的整数 ∴当x=7时, 即下半年7月份出售每千克的利润最大,最大利润是。 24.(1) 解:作点B关于AC的对称点B,连接BE交AC于P, 此时PB+PE的值最小. 连接AB. AB=AB= AE= ∵∠BAC=∠BAC=45 ∴∠BAB=90 ∴PB+PE的最小值= BE= (2)作点B关于AC的对称点B,过B作BN⊥AB于N,交AC于M.此时BM+MN的值最小. BM+MN=BN. 理由:如图1,在AC上任取一点M(不与点M重合), 在AB上任取一点N, 连接B M、B M、M N、B N. ∵点B与点B关于AC对称 ∴B M= B M ∴B M+ M N= B M+ M N> B N 又∵B N> BN,BM+MN=BN ∴B M+ M N> BM+MN 计算:如图2 ∵点B与点B关于AC对称 ∴A B=AB 又∵∠BAC=30 ∴∠BAB=60 图2 ∴△BAB是等边三角形 ∴BB=AB=2,∠BBN=60 又∵BN⊥AB ∴BN= BB= (3)方法一:构造图形如图所示 其中:AB=4,AC=1,DB=2,AC=x,CA⊥AB于A,DB⊥AB于B. 那么PC+PD= 所求的最小值就是求PC+PD的 最小值. 作点C关于AB的对称点C,过C作CE垂直DB的延长线于E。 则CE=AB=4,DE=2+1=3,CD= 所求的最小值是5. 方法二:构造图形如图所示 在直角坐标系中,点A(0,1)、B(4,2)、P(x,0) (0≤x≤4) 那么PA+PB= 所求的最小值就是求PA+PB的 最小值. 作点C关于x轴的对称点A,过A作AC垂直于 y轴,过点B作BC垂直于x轴交AC于点C。 则AC=4,BC=3,AB= 所求的最小值是5. 25.解:(1)①方法一: ∵四边形ABCD是矩形,AB∥x轴,B(-3,3) ∴A( C() ∵y=经过A、C两点 ∴ ∴ ∵ ∴ ∴ 方法二:∵四边形ABCD是矩形,AB∥x轴,B(-3,3) ∴A( C() D( ∴AB=,AD= ∴AB=AD 四边形ABCD是正方形,∴∠AEO=∠ACD=45 ∴OE=OF=b E(-b,0) ∴ ∵ ∴ ②∵S=S=S ∴S= ∴当k> 时,S随着k的增大而增大. 又∵k>0,k没有最小值,∴S没有最小值. (2)答:AE=CF,理由如下: 方法一:连接MN,设AB交y轴于P点,BC角x轴于Q点. ∵S ∴ ∴ 又∵∠D=∠D ∴△DNM∽△DCA ∴∠DNM=∠DCA ∴AF=MN ∴MN∥AC 同理CE=MN 又∵AD∥y轴 ∴AF=CE ∴四边形AFNM是平行四边形 ∴AE=CF 方法二:设A(、C 则AM=,AD=,CN=-,CD= ∵EM∥CD 又∵FN∥AD ∴△AEM∽△ACD ∴△CFN∽△CAD ∴ ∴ ∴ ∴ ∴AE=CF 方法三:设A(、C 则M(m,0)、N(0,). 则 ∴ ∴ 直线AC为: ∴E(m+n,0) ∴EM= ∵CN=- ∴EM=CN ∵EM∥BA∥CN ∴∠AEM=∠FCN 又∵∠AME=∠FNC=90 ∴△AEM≌△FCN ∴AE=CF查看更多