深圳十年中考数学压轴题汇总

深圳十年中考数学压轴题汇总

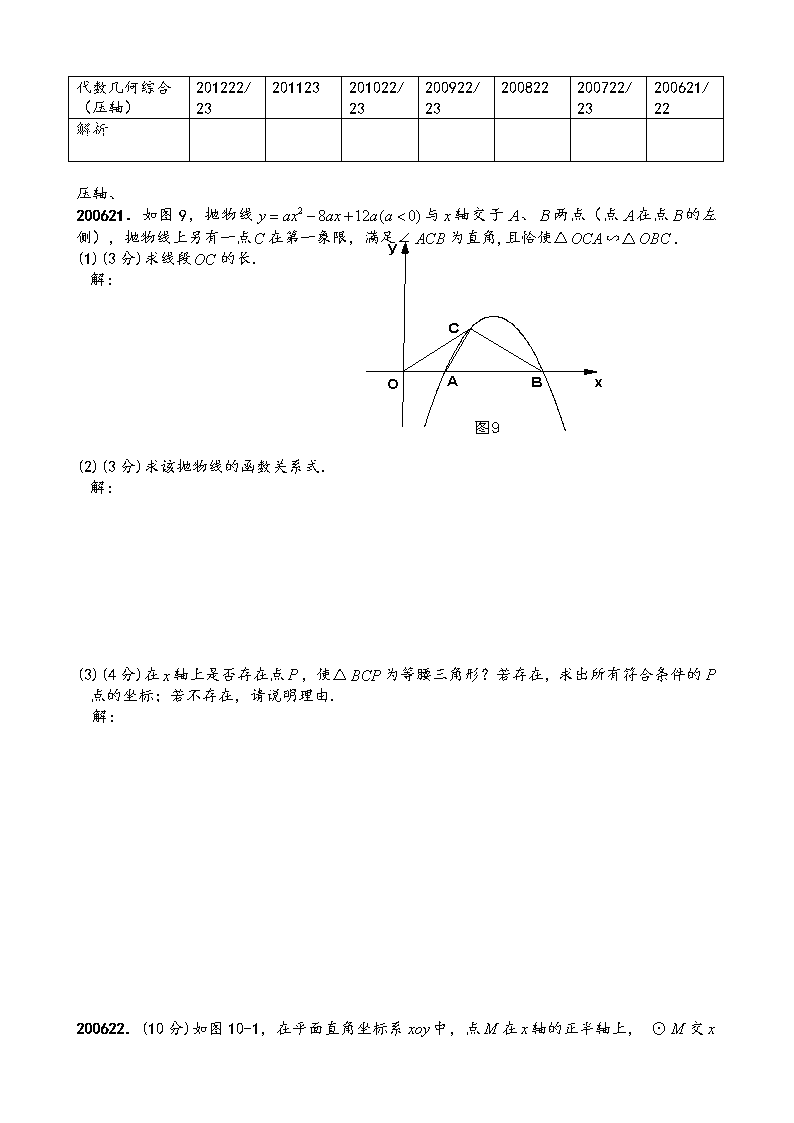
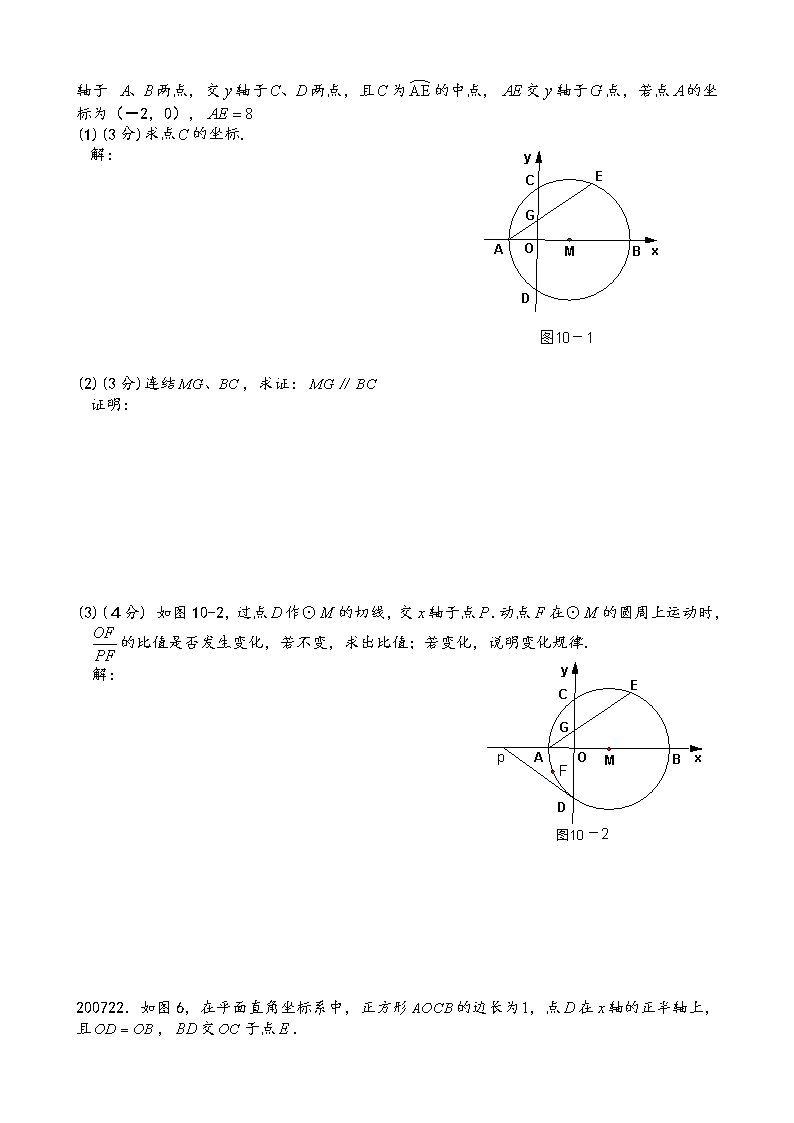
代数几何综合（压轴）‎ ‎201222/23‎ ‎201123‎ ‎201022/23‎ ‎200922/23‎ ‎200822‎ ‎200722/23‎ ‎200621/22‎ 解析 压轴、‎ ‎200621．如图9，抛物线与轴交于、两点（点在点的左侧），抛物线上另有一点在第一象限，满足∠为直角,且恰使△∽△.‎ ‎(1)(3分)求线段的长.‎ 解：‎ ‎ ‎ ‎(2)(3分)求该抛物线的函数关系式．‎ 解：‎ ‎(3)(4分)在轴上是否存在点，使△为等腰三角形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由.‎ ‎ 解： ‎ ‎200622．(10分)如图10-1，在平面直角坐标系中，点在轴的正半轴上， ⊙交 轴于 两点，交轴于两点，且为的中点，交轴于点，若点的坐标为（－2，0），‎ ‎(1)(3分)求点的坐标. ‎ 解：‎ ‎(2)(3分)连结，求证：∥‎ 证明：‎ ‎(3)(４分) 如图10-2，过点作⊙的切线，交轴于点.动点在⊙的圆周上运动时，的比值是否发生变化，若不变，求出比值；若变化，说明变化规律.‎ ‎ 解： ‎ ‎200722．如图6，在平面直角坐标系中，正方形的边长为，点在轴的正半轴上，且，交于点．‎ ‎（1）求的度数．‎ ‎（2）求点的坐标．‎ ‎（3）求过三点的抛物线的解析式．（计算结果要求分母有理化．参考资料：把分母中的根号化去，叫分母有理化．例如：①；‎ 图6‎ ‎②；③等运算都是分母有理化）‎ ‎200723．如图7，在平面直角坐标系中，抛物线与直线相交于两点．‎ ‎（1）求线段的长．‎ ‎（2）若一个扇形的周长等于（1）中线段的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少？‎ ‎（3）如图8，线段的垂直平分线分别交轴、轴于两点，垂足为点，分别求出的长，并验证等式是否成立．‎ 图7‎ 图8‎ ‎（4）如图9，在中，，，垂足为，设，，．，试说明：．‎ 图9‎ ‎200822．如图9，在平面直角坐标系中，二次函数的图象的顶点为D点，‎ 与y轴交于C点，与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），‎ OB＝OC ，tan∠ACO＝．‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．‎ ‎（3）若平行于x轴的直线与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度．‎ ‎（4）如图10，若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.‎ ‎ ‎ ‎200922．如图，在直角坐标系中，点A的坐标为（－2，0），连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB.‎ ‎（1）求点B的坐标；‎ ‎（2）求经过A、O、B三点的抛物线的解析式；‎ ‎（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.‎ B A O y x ‎（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.‎ ‎200923．如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.‎ ‎（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；‎ ‎（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎201022．（本题9分）如图9，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1, －3）．‎ ‎ （1）求抛物线的解析式；（3分）‎ ‎（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；（2分）‎ ‎（3）在第（2）问的结论下，抛物线上的点P使S△PAD＝4S△ABM成立，求点P 的坐标．（4分）‎ x y C B ‎_‎ D ‎_‎ A O 图9‎ ‎201023．（本题9分）如图10，以点M（－1,0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－ x－ 与⊙M相切于点H，交x轴于点E，交y轴于点F．‎ ‎ （1）请直接写出OE、⊙M的半径r、CH的长；（3分）‎ ‎（2）如图11，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；（3分）‎ ‎（3）如图12，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．（3分）‎ ‎ ‎x D A B H C E M O F 图10‎ x y D A B H C E M O F 图11‎ P Q x y D A B H C E M O F 图12‎ N T K y ‎201123．如图13，抛物线y＝ax2＋bx＋c（a≠0）的顶点为C（1，4），交x轴于A、B两点，‎ 交y轴于点D，其中点B的坐标为（3，0）。‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图14，过点A的直线与抛物线交于点E，交y轴于点F，其中点E的横坐标为2，若直线PQ为抛物线的对称轴，点G为直线PQ上的一动点，则x轴上师范存在一点H，使D、G、H、F四点所围成的四边形周长最小。若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由。‎ ‎（3）如图15，在抛物线上是否存在一点T，过点T作x轴的垂线，垂足为点M，过点M作MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD。若存在，求出点T的坐标；若不存在，请说明理由。‎ 图13‎ A B x y O D C 图14‎ A B x y O D C P Q E F 图15‎ A B x y O D C ‎201222．如图8，已知△ABC的三个顶点坐标分别为 ‎（1）求经过A、B、C三点抛物线的解析式 ‎（2）设直线BC交y轴于点E，连接AE，求证：AE=CE 图8‎ ‎（3）设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与△ABC相似吗？请说明理由。‎ ‎201223．如图9—①，平在面直角从标系中，直线的位置随的不同取值而变化。‎ ‎（1）已知⊙M的圆心坐标为（4，2），半径为2‎ ‎ 当 时，直线经过圆心M；‎ 当 时，直线与 ⊙M相切；‎ 图9—②‎ ‎（2）若把⊙M换成矩形，如图9—②，其三个顶点的坐标分别为：‎ ‎。设直线扫过矩形的面积为，当由小到大变化时，请求出与的函数关系式。‎ 图9—①‎