苏教版数学七年级上册课件4-2解一元一次方程（2）

苏教版数学七年级上册课件4-2解一元一次方程（2）

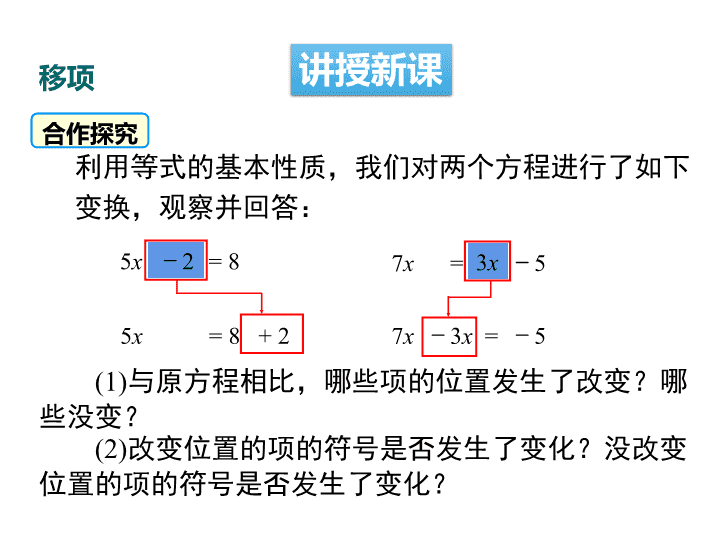
4.2解一元一次方程（2） 情境引入 约公元825年，中亚细亚数学 家阿尔—花拉子米写了一本 代数书，重点论述了怎么解 方程.这本书的拉丁译本为 《对消与还原》，“对消”与 “还原”是什么意思呢？ 导入新课 合作探究 (1)与原方程相比，哪些项的位置发生了改变？哪 些没变？ (2)改变位置的项的符号是否发生了变化？没改变 位置的项的符号是否发生了变化？ 5x －2 = 8 5x = 8 + 2 7x = 3x －5 7x －3x = －5 利用等式的基本性质，我们对两个方程进行了如下 变换，观察并回答： 讲授新课移项 归纳： 方程中的某些项改变________后，可以从 ________的一边移到________，这样的变形叫 作移项. (1)移项的根据是等式的基本性质1. (2)移项要变号，没有移动的项不改变符号. (3)通常把含有未知数的项移到方程的左边，把 常数项(不含未知数的项)移到方程的右边. 移项要点： 符号 方程 另一边 例1 下列计算，其中属于移项变形的是（ ） 典例精析 [解析]利用移项的要点解题，A是代数式变形， 不是移项；B移项时符号错了；D不是移项． C A.由5+3x-2,得3x-2+5 B.由－10x－5＝－2x，得－10x－2x＝5 C.由7x＋9＝4x－1，得7x－4x＝－1－9 D.由5x＝9，得x＝ 9 5 1.移项时必须是从等号的一边到另一边，并且不 要忘记对移动的项变号，如从2＋5x＝7得到5x＝7 ＋2是不对的． [易错提醒] 2.没移项时不要误认为移项，如从－8＝x得到x＝8， 犯这样的错误，其原因在于对等式的基本性质(对 称性)与移项的区别没有分清． (1)5＋x＝10移项得x＝ 10＋5 ； (2)6x＝2x＋8移项得 6x＋2x ＝8； (3)5－2x＝4－3x移项得3x－2x＝4－5； (4)－2x＋7＝1－8x移项得－2x＋8x＝1－7. 做一做 × × √ √ 10－5 － 下面的移项对不对？如果不对，应怎样改正？ 议一议 小明在解方程x－4＝7时，求解过程是这样 写的：x－4＝7＝x＝7＋4＝x＝11. (1)小明这样写对不对？为什么？ (2)应该怎样写？ 解：(1)不对．因为解方程是对一个含有未 知数的等式进行变形的过程，不能连等． (2)移项，得x＝7＋4. 化简，得x＝11. 利用移项、合并同类项解方程 解：(1)移项，得 2x=1－6. 化简，得 2x=－5. 方程两边同除以2，得 x= . (2)移项，得 3x－2x=7－3. 合并同类项，得 x=4. 5 2  例2 解下列方程： (1) 2x+6=1; (2)3x+3=2x+7; 解：移项，得 方程两边同除以 ，得 合并同类项，得 你能说出利用 移项解方程的 步骤吗？ 1 1(3) - 3. 4 2 x x  1 1 3. 4 2 x x  3 3. 4 x  3 4 4.x  (1)移项； [归纳总结] 利用移项解方程的步骤是 (3)系数化为1. (2)合并同类项； 练一练 解：(1)移项，得 4x－2x=3－7. 方程两边同除以2，得 x=－2. 合并同类项，得 2x=－4. (2)移项，得 x－x=－1. 方程两边同乘－4，得 x=4. 合并同类项，得 － x=－1. 3 4 1 4 用移项法解下列方程： (1) 7-2x=3-4x; (2) 3 3. 4 x x  例3 做一做 3 例2 某制药厂制造一批药品，如果用旧工艺，则 废水排量要比环保限制的最大量还多200 t；如果 用新工艺，则废水排量要比环保限制的最大量少 100 t.新旧工艺的废水排量之比为2 ：5，两种工艺 的废水排量各是多少？ 思考：①如何设未知数？ ②你能找到等量关系吗？ 列方程解决问题 旧工艺废水排量－200吨=新工艺排水量+100吨 解：若设新工艺的废水排量为5x吨，则旧工艺的 废水排量为2x吨；由题意得到的等量关系： 可列方程为： 移项，得 系数化为1，得 所以 合并同类项，得 答：新工艺的废水排量为 200 吨，则旧工艺的废 水排量为 500 吨； 5x-200=2x+100, 5x-2x=200+100, 3x=300, x=100, 2x=200,5x=500. 1.下面是两种移动电话计费方式： 方式一 方式二 月租费 50元/月 10元/月 本地通话费 0.30元/分 0.5元/分 问：一个月内，通话时间是多少分钟时， 两种移动电话计费方式的费用一样？ 练一练 解：设通话时间t分钟,则按方式一要收费 （50+0.3t）元，按方式二要收费（10＋0.4t）. 如果两种移动电话计费方式的费用一样， 则 50+0.3t＝ 10＋0.4t 移项，得 0.3t-0.4t=10－50 合并同类项，得 －0.1t=－40. 　　系数化为1，得t=400. 　　答：一个月内通话400分钟时，两种计费方 式的费用一样. 2.小明和小刚每天早晨坚持跑步，小明每秒跑4米， 小刚每秒跑6米.若小明站在百米起点处，小刚站在他前 面10米处，两人同时同向起跑，几秒后小明追上小刚？ 4 x 10 6 x 解：设小明x秒后追上小刚. 可得方程：4x＋10＝6x 移项，得 4x－6x＝－10 合并同类项，得 －2x＝－10 系数化为1,得 x＝5. 答：小明5秒后追上小刚. 1.方程6x=3+5x的解是(　　) A.x=2 B.x=3 C.x=-2 D.x=-3 2.方程 的解是( ) A.x=1 B.x=-1 C.x=4 D.x=0 1 1x 2 2 x 2 2    3.方程2x-4=0的解是________. B C x=2 随堂练习 5.若5a＋2与7－2a的和是15，求a的值. 6.已知x＋6与2x－3的值是相反数，求x的值. 4.已知x=3是方程mx－5=3＋m的解，求m. 3m-5=3+m 2m=8 m=4 5a+2+7-2a=15 3a=6 a=2 x+6+2x-3=0 3x=-3 x=-1 7.把一批图书分给七年级某班的同学阅读，若每 人分3本，则剩余20本，若每人分4本，则缺25本， 这个班有多少学生？ 解：设这个班有x个学生， 根据题意得 3x＋20＝4x－25， 移项得 3x－4x＝－25－20， 合并同类项得 －x＝－45， 系数化成1得x＝45. 答：这个班有45人. 解下列方程:4|x|-3=6. 方程两边同时除以4， 得： 解：移项，得： 合并，得： 拓展提升 4|x|=6+3. 4|x|=9. 9| | 4 x  9 . 4 x  所以 利用移项与合 并同类项解一 元一次方程 移项 { 利用移项解方程 移项的概念 移项法则 { 移项 系数化1 {合并同类项 课堂小结