2021高三数学人教B版一轮学案：第八章 第六节　双曲线

2021高三数学人教B版一轮学案：第八章 第六节　双曲线

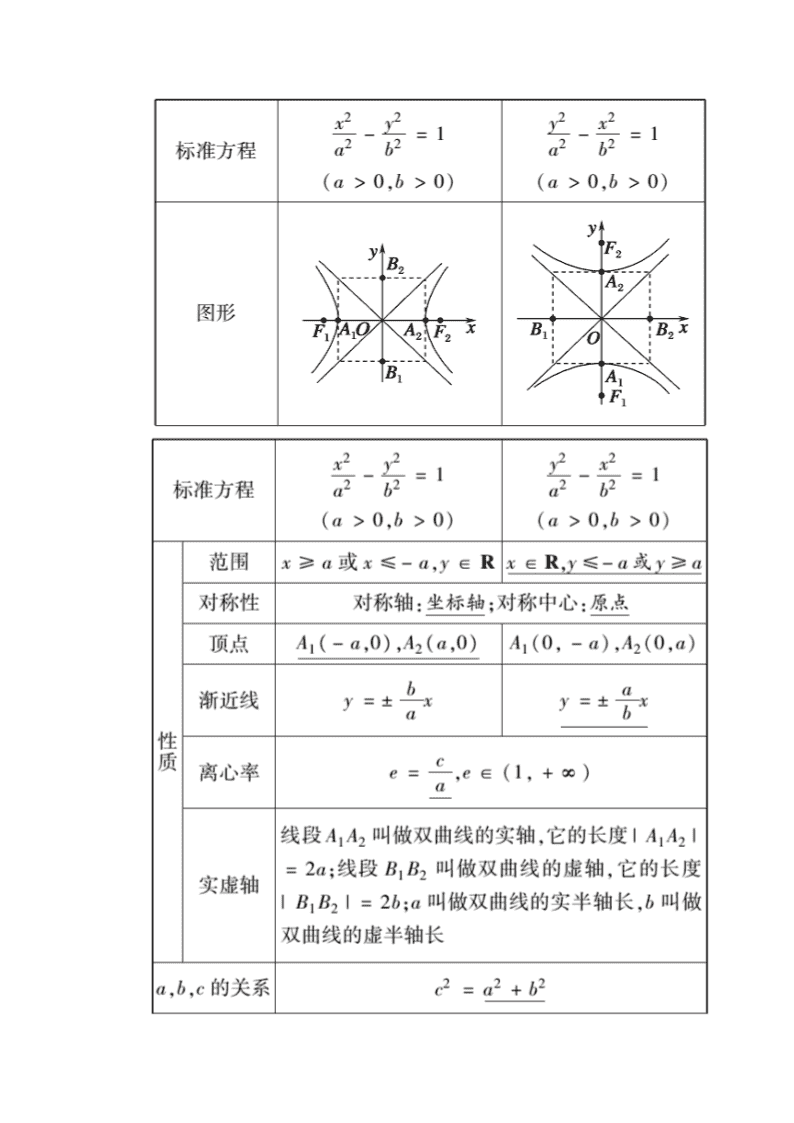
www.ks5u.com 第六节　双曲线 最新考纲 考情分析 ‎1.了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线)．‎ ‎2．了解双曲线的简单应用．‎ ‎3．理解数形结合的思想.‎ ‎1.双曲线的定义、标准方程、几何性质是近几年高考命题的热点．‎ ‎2．常与圆、椭圆、抛物线等知识交汇命题．‎ ‎3．题型以选择题、填空题为主，属中低档题.‎ ‎　　　　　　　　　　　　　　　　‎ 知识点一　　双曲线的定义 平面内与两个定点F1，F2(|F‎1F2|＝‎2c>0)的距离差的绝对值等于常数(小于|F‎1F2|且大于零)的点的轨迹叫双曲线．这两个定点叫双曲线的焦点，两焦点间的距离叫焦距．其数学表达式：集合P＝{M|||MF1|－|MF2||＝‎2a}，|F‎1F2|＝‎2c，其中a，c为常数且a>0，c>0：‎ ‎(1)若ac，则集合P为空集．‎ 知识点二　　双曲线的标准方程和几何性质 ‎1.过双曲线的一个焦点且与实轴垂直的弦的长为.‎ ‎2．离心率e＝＝＝.‎ ‎3．等轴双曲线的渐近线互相垂直，离心率等于.‎ ‎1．思考辨析 判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)平面内到两点F1(－1,0)，F2(1,0)的距离之差等于1的点的轨迹是双曲线．(　×　)‎ ‎(2)方程－＝1(mn>0)表示焦点在x轴上的双曲线．(　×　)‎ ‎(3)与双曲线－＝1(mn>0)共渐近线的双曲线方程可设为－＝λ(λ≠0)．(　√　)‎ ‎(4)等轴双曲线的离心率等于，且渐近线互相垂直．(　√　)‎ ‎(5)若双曲线－＝1(a>0，b>0)与－＝1(a>0，b>0)的离心率分别是e1，e2，则＋＝1(此结论中两条双曲线为共轭双曲线)．(　√　)‎ 解析：(1)已知点的轨迹是双曲线的一支．到两点F1(－1,0)，F2(1,0)的距离之差的绝对值为1的点的轨迹是双曲线．‎ ‎(2)例如当m＝－1，n＝－1时，方程为y2－x2＝1，表示焦点在y轴上的双曲线．‎ ‎(3)易知双曲线－＝1与－＝λ(λ≠0)渐近线相同，且－＝λ(λ≠0)可表示渐近线为y＝±x的任意双曲线．‎ ‎(4)因为是等轴双曲线，所以a＝b，c＝a，离心率等于 ‎.渐近线方程为y＝±x，互相垂直．‎ ‎(5)由已知，e＝＝，e＝＝，‎ 所以＋＝＋＝1.‎ ‎2．小题热身 ‎(1)双曲线－＝1的焦距为(　C　)‎ A．5　　 　 　B. C．2　　 　D．1‎ 解析：∵c2＝3＋2＝5，c＝，所以焦距‎2c＝2.‎ ‎(2)设P是双曲线－＝1上一点，F1，F2分别是双曲线左、右两个焦点，若|PF1|＝9，则|PF2|等于(　B　)‎ A．1 B．17‎ C．1或17 D．以上答案均不对 解析：由题意知|PF1|＝95 B．25‎ 解析：由题意知，(|k|－2)(5－k)<0，解得－25.‎ ‎(4)双曲线－＝1(a>0，b>0)的离心率为，则其渐近线方程为y＝±x.‎ 解析：解法1：由题意知，e＝＝，所以c＝a，所以b＝＝a，所以＝，所以该双曲线的渐近线方程为y＝±x＝±x.‎ 解法2：由e＝＝＝，得＝，所以该双曲线的渐近线方程为 y＝±x＝±x.‎ ‎(5)若双曲线－＝1(a>0，b>0)的一条渐近线被圆x2＋y2－6x＋5＝0所截得的弦的长为2，则该双曲线的离心率等于.‎ 解析：不妨取双曲线－＝1的一条渐近线方程为bx－ay＝0，圆x2＋y2－6x＋5＝0的圆心为(3,0)，半径为2，∴圆心(3,0)到渐近线bx－ay＝0的距离d＝，又d＝＝，∴＝，化简得a2＝2b2，∴该双曲线的离心率e＝＝＝＝.‎ ‎　　　　　　　　　　　　　　　　‎ 考点一　双曲线的定义及应用 ‎【例1】　(1)已知F1，F2为双曲线C：x2－y2＝1的左、右焦点，点P在C上，∠F1PF2＝60°，则|PF1|·|PF2|等于(　　)‎ A．2 B．4‎ C．6 D．8‎ ‎(2)已知圆C：(x－3)2＋y2＝4，定点A(－3,0)，则过定点A且和圆C外切的动圆圆心M的轨迹方程为________．‎ ‎【解析】　(1)由双曲线的方程得a＝1，c＝，由双曲线的定义得||PF1|－|PF2||＝2.在△PF‎1F2中，由余弦定理得|F‎1F2|2＝|PF1|2＋|PF2|2－2|PF1|·|PF2|cos60°，即(2)2＝|PF1|2＋|PF2|2－|PF1|·|PF2|＝(|PF1|－|PF2|)2＋|PF1|·|PF2|＝22＋|PF1|·|PF2|.解得|PF1|·|PF2|＝4.故选B.‎ ‎(2)设动圆M的半径为R，则|MC|＝2＋R，|MA|＝R，∴|MC|－|MA|＝2，由双曲线的定义知，M点的轨迹是以A，C 为焦点的双曲线的左支，且a＝1，c＝3，∴b2＝8，则动圆圆心M的轨迹方程为x2－＝1(x≤－1)．‎ ‎【答案】　(1)B　(2)x2－＝1(x≤－1)‎ 方法技巧 双曲线定义的主要应用方面 ‎(1)判定平面内动点与两定点的轨迹是否为双曲线，进而根据要求可求出曲线方程．‎ ‎(2)在“焦点三角形”中，常利用正弦定理、余弦定理，结合||PF1|－|PF2||＝‎2a，运用平方的方法，建立与|PF1|·|PF2|的联系．‎ ‎1．(2020·安徽省五校联盟质量检测)－＝4表示的曲线方程为(　C　)‎ A.－＝1(x≤－2)‎ B.－＝1(x≥2)‎ C.－＝1(y≤－2)‎ D.－＝1(y≥2)‎ 解析：的几何意义为点M(x，y)到点F1(0,3)的距离，的几何意义为点M(x，y)到点F2(0，－3)的距离，则－＝4表示点M(x，y)到点F1(0,3)的距离与到点F2(0，－3)的距离的差为4，且4<|F‎1F2|，所以点M的轨迹是以F1，F2为焦点的双曲线的下支，且该双曲线的实半轴长a＝2，半焦距c＝3，所以b2＝c2－a2＝5，则－＝4表示的曲线方程为 ‎－＝1(y≤－2)，故选C.‎ ‎2．(2020·南昌市第一次模拟)已知A(－，0)，B(，0)，P为圆x2＋y2＝1上的动点，＝，过点P作与AP垂直的直线l交直线QB于点M，若点M的横坐标为x，则|x|的取值范围是(　A　)‎ A．|x|≥1 B．|x|>1‎ C．|x|≥2 D．|x|≥ 解析：如图，由题意得，||MB|－|MA||＝|QB|＝2|OP|＝2，所以点M的轨迹是以A，B为左、右焦点的双曲线，且a＝1，所以|x|的取值范围是|x|≥1，故选A.‎ 考点二　双曲线的标准方程 ‎【例2】　(1)已知双曲线C：－＝1(a>0，b>0)的上焦点为F，M是双曲线的虚轴的一个端点，过F，M的直线交双曲线的下支于A点．若M为AF的中点，且||＝6，则双曲线C的方程为(　　)‎ A.－＝1 B.－＝1‎ C．y2－＝1 D.－x2＝1‎ ‎(2)已知圆C1：(x＋3)2＋y2＝1和圆C2：(x－3)2＋y2＝9，动圆M同时与圆C1及圆C2相外切，则动圆圆心M的轨迹方程为________．‎ ‎【解析】　(1)由题知，F(0，c)，根据对称性，设M(b,0)，又M为AF的中点，则A(2b，－c)，由题意可得 解得所以双曲线C的方程为y2－＝1，故选C.‎ ‎(2)如图所示，设动圆M与圆C1及圆C2分别外切于A和B.根据两圆外切的条件，得|MC1|－|AC1|＝|MA|，|MC2|－|BC2|＝|MB|，因为|MA|＝|MB|，所以|MC1|－|AC1|＝|MC2|－|BC2|，即|MC2|－|MC1|＝|BC2|－|AC1|＝2，‎ 所以点M到两定点C2，C1的距离的差是常数且小于|C‎1C2|＝6.‎ 又根据双曲线的定义，得动点M的轨迹为双曲线的左支(点M与C2的距离大，与C1的距离小)，其中a＝1，c＝3，则b2＝8.‎ 故点M的轨迹方程为x2－＝1(x≤－1)．‎ ‎【答案】　(1)C　(2)x2－＝1(x≤－1)‎ 方法技巧 求双曲线标准方程的两种方法 待定 系数法 设出双曲线方程的标准形式，根据已知条件，列出参数a，b，c的方程并求出a，b，c的值 定义法 依定义得出距离之差的等量关系式，求出a的值，由定点位置确定c的值 求双曲线的标准方程时，若焦点位置不确定，要注意分类讨论．也可以设双曲线方程为mx2＋ny2＝1(mn<0)求解．‎ ‎1．已知双曲线－＝1(a>0，b>0)的左、右焦点分别为F1，F2，点P在双曲线的右支上，若|PF1|－|PF2|＝4b，且双曲线的焦距为2，则该双曲线的标准方程为(　A　)‎ A.－y2＝1 B.－＝1‎ C．x2－＝1 D.－＝1‎ 解析：由题意可得 解得则该双曲线的标准方程为－y2＝1.‎ ‎2．设椭圆C1的离心率为，焦点在x轴上且长轴长为26，若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8，则曲线C2的标准方程为－＝1.‎ 解析：由题意知椭圆C1的焦点坐标为F1(－5,0)，F2(5,0)，设曲线C2上的一点P，则||PF1|－|PF2||＝8.‎ 由双曲线的定义知，a＝4，b＝3.‎ 故曲线C2的标准方程为－＝1.‎ 即－＝1.‎ 考点三　双曲线的几何性质 命题方向1　　与渐近线有关的问题 ‎【例3】　(1)(2020·武汉市调研测试)已知双曲线－＝1(b>0)的渐近线方程为x±y＝0，则b＝(　　)‎ A．2　　　　B. C.　　　　D．12‎ ‎(2)(2020·河南鹤壁高中模拟)设F1，F2是双曲线C：－＝1(a>0，b>0)的左、右焦点，P是双曲线C右支上一点，若|PF1|＋|PF2|＝‎4a，且∠F1PF2＝60°，则双曲线C的渐近线方程是(　　)‎ A.x±y＝0 B．2x±y＝0‎ C.x±2y＝0 D．2x±y＝0‎ ‎【解析】　(1)依题意，得＝，所以b＝2，故选A.‎ ‎(2)∵F1，F2是双曲线的左、右焦点，点P在双曲线右支上，∴由双曲线定义可得|PF1|－|PF2|＝‎2a，又知|PF1|＋|PF2|＝‎4a，‎ ‎∴|PF1|＝‎3a，|PF2|＝a.在△PF‎1F2中，由余弦定理的推论可得cos60°＝，‎ 即＝，‎ ‎∴‎3a2＝‎10a2－‎4c2，即‎4c2＝‎7a2，又知b2＋a2＝c2，∴＝，∴双曲线C的渐近线方程为y＝±x，即x±2y＝0，故选C.‎ ‎【答案】　(1)A　(2)C 命题方向2　　求离心率的值或范围 ‎【例4】　(2019·全国卷Ⅰ)已知双曲线C：－＝1(a>0，b>0)的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若＝，·＝0，则C的离心率为________．‎ ‎【解析】　解法1：因为·＝0，所以F1B⊥F2B，如图．‎ 所以|OF1|＝|OB|，所以∠BF1O＝∠F1BO，所以∠BOF2＝2∠BF1O.因为＝，所以点A为F1B的中点，又点O为F‎1F2的中点，所以OA∥BF2，所以F1B⊥OA，因为直线OA，OB为双曲线C的两条渐近线，所以tan∠BF1O＝，tan∠BOF2＝.因为tan∠BOF2＝tan(2∠BF1O)，所以＝，所以b2＝‎3a2，所以c2－a2＝‎3a2，即‎2a＝c，所以双曲线的离心率e＝＝2.‎ 解法2：因为·＝0，所以F1B⊥F2B，在Rt△F1BF2中，|OB|＝|OF2|，所以∠OBF2＝∠OF2B，又＝，所以A为F1B的中点，所以OA∥F2B，所以∠F1OA＝∠OF2B.又∠F1OA＝∠BOF2，所以△OBF2为等边三角形．由F2(c,0)可得B(，)，因为点B在直线y＝x上，所以c＝·，所以＝，所以e＝＝2.‎ ‎【答案】　2‎ 方法技巧 ‎1.求双曲线的渐近线 一般是根据渐近线定义求解，求出a，b的值或a与b的比值，进而求得双曲线的渐近线.‎ ‎2.求双曲线离心率的方法 (1)直接求出a，c的值，利用离心率公式直接求解.‎ (2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝a2－c2消去b，转化为含有e的方程(或不等式)求解，注意e的取值范围.‎ ‎1．(方向1)若双曲线C1：－＝1与C2：－＝1(a>0，b>0)的渐近线相同，且双曲线C2的焦距为4，则b＝(　B　)‎ A．2　　　 　B．‎4　‎　 　　C．6 　　　　D．8‎ 解析：C1的渐近线方程为y＝±2x，即＝2，又因为‎2c＝4，c＝2.由c2＝a2＋b2得，所以20＝b2＋b2，解得b＝4.‎ ‎2．(方向2)(2019·全国卷Ⅱ)设F为双曲线C：－＝1(a>0，b>0)的右焦点，O为坐标原点，以OF为直径的圆与圆x2＋y2＝a2交于P，Q两点．若|PQ|＝|OF|，则C的离心率为(　A　)‎ A. B. C．2 D. 解析：如图，由题意，知以OF为直径的圆的方程为(x－)2＋y2＝①，将x2＋y2＝a2记为②式，①－②得x＝，则以OF为直径的圆与圆x2＋y2＝a2的相交弦所在直线的方程为x＝，所以|PQ|＝2.由|PQ|＝|OF|，得2＝c，整理得c4－‎4a2c2＋‎4a4＝0，即e4－4e2＋4＝0，解得e＝，故选A.‎ ‎3．(方向1)已知F1，F2为双曲线－＝1(a>0，b>0)的焦点，过F2作垂直于x轴的直线交双曲线于点P和Q且△F1PQ为正三角形，则双曲线的渐近线方程为y＝±x.‎ 解析：设F2(c,0)(c>0)，P(c，y0)，‎ 代入双曲线方程得y0＝±，‎ 因为PQ⊥x轴，所以|PQ|＝.‎ 在Rt△F‎1F2P中，∠PF‎1F2＝30°，‎ 所以|F‎1F2|＝|PF2|，即‎2c＝·，‎ 又因为c2＝a2＋b2，所以b2＝‎2a2或‎2a2＝－3b2(舍)，又因为a>0，b>0，‎ 所以＝，所以所求双曲线的渐近线方程为y＝±x.‎ ‎　　　　　　　　　　　　　　　　‎ 经久不衰的高考热点——离心率问题 离心率是圆锥曲线的重要几何性质，是高考重点考查的一个知识点．这类问题一般有两类：一类是根据一定的条件求圆锥曲线的离心率；另一类是根据一定的条件求离心率的取值范围，无论是哪类问题，其难点都是建立关于a，b，c的关系式(等式或不等式)，并且最后要把其中的b用a，c表示，转化为关于离心率e的关系式，这是化解有关椭圆或双曲线的离心率问题难点的根本方法．‎ 类型一　利用定义求离心率 ‎【典例1】　在直角坐标系xOy中，设F为双曲线C：－＝1(a>0，b>0)的右焦点，P为双曲线C的右支上一点，且△OPF为正三角形，则双曲线C的离心率为(　　)‎ A. B. C．1＋ D．2＋ ‎【解题思路】　设F′为双曲线的左焦点，利用△OPF为正三角形求出|PO|＝|PF|＝c，∠POF′＝120°，利用双曲线的定义得到|PF′|＝‎2a＋c，最后在△PF′O中由余弦定理可得的值．‎ ‎【解析】　设F′为双曲线的左焦点，|F′F|＝‎2c，依题意可得|PO|＝|PF|＝c，连接PF′，由双曲线的定义可得|PF′|‎ ‎－|PF|＝‎2a，故|PF′|＝‎2a＋c，在△PF′O中，∠POF′＝120°，由余弦定理可得cos120°＝，化简可得c2－‎2ac－‎2a2＝0，即()2－2×－2＝0，解得＝1＋或＝1－(不合题意，舍去)，故双曲线的离心率e＝1＋，故选C.‎ ‎【答案】　C ‎1．(2020·湖南省五市十校联考)已知A，B，C是双曲线－＝1(a>0，b>0)上的三个点，直线AB经过原点O，AC经过右焦点F，若BF⊥AC，且3|AF|＝|CF|，则该双曲线的离心率为(　A　)‎ A. B. C. D. 解析：如图，设双曲线的左焦点为E，连接AE，CE，BE，‎ 由题意知|BF|＝|AE|，|BE|＝|AF|，四边形AEBF为矩形，‎ 令|BF|＝|AE|＝m，|AF|＝n，‎ 由双曲线的定义，得 ‎|CE|－|CF|＝|AE|－|AF|＝‎2a，‎ 在直角三角形EAC中，m2＋(3n＋n)2＝(3n＋‎2a)2，‎ 将‎2a＝m－n代入，化简，可得m＝3n，‎ 又m－n＝‎2a，所以n＝a，m＝‎3a，‎ 在直角三角形EAF中，m2＋n2＝(‎2c)2，即‎9a2＋a2＝‎4c2，可得e＝＝.故选A.‎ 类型二　利用平面几何性质求离心率 ‎【典例2】　已知椭圆M：＋＝1(a>b>0)，双曲线N：－＝1.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为________；双曲线N的离心率为________．‎ ‎【解析】　如图，设椭圆的右焦点为F(c,0)，双曲线N的渐近线与椭圆M在第一象限内的交点为A，由题意可知A(，)，由点A在椭圆M上得，＋＝1，∴b‎2c2＋‎3a2c2＝‎4a2b2，∵b2＝a2－c2，∴(a2－c2)c2＋‎3a2c2＝‎4a2(a2－c2)，∴‎4a4－‎8a2c2＋c4＝0，‎ ‎∴e－8e＋4＝0，∴e＝4±2，∴e椭＝＋1(舍去)或e椭＝－1，∴椭圆M的离心率为－1，∵双曲线的渐近线过点A(，)，∴渐近线方程为y＝x，∴＝，故双曲线的离心率e双＝＝2.‎ ‎【答案】　－1　2‎ ‎2．(2020·福州市质量检测)如图，双曲线C：－＝1(a>0，b>0)的左、右焦点分别为F1，F2，过F2作直线与C的渐近线交于P点，若等腰△PF‎1F2的底边PF2的长等于C的半焦距，则C的离心率为(　C　)‎ A. B. C. D. 解析：依题意，kOP＝＝＝，在等腰△PF‎1F2中，cos∠PF‎2F1＝＝＝，所以|OP|2＝c2＋c2－‎2c2cos∠PF‎2F1＝c2，所以|OP|＝‎ eq f(r(6),2)c，所以cos∠F2OP＝＝，所以tan∠F2OP＝，所以＝，解得e＝，故选C.‎ 类型三　利用椭圆或双曲线的性质建立方程(或不等式)求离心率的值(或取值范围)‎ ‎【典例3】　已知F1(－c,0)，F2(c,0)为椭圆＋＝1(a>b>0)的两个焦点，点P在椭圆上且满足·＝c2，则该椭圆离心率的取值范围是(　　)‎ A. B. C. D. ‎【解析】　设P(x，y)，则＋＝1(a>b>0)，y2＝b2－x2，－a≤x≤a，＝(－c－x，－y)，＝(c－x，－y)．所以·＝x2－c2＋y2＝x2＋b2－c2＝x2＋b2－c2.因为－a≤x≤a，所以b2－c2≤·≤b2.所以b2－c2≤c2≤b2，所以‎2c2≤a2≤‎3c2，所以≤≤.故选B.‎ ‎【答案】　B ‎3．已知椭圆E：＋＝1(a>b>0)的右焦点为F，短轴的一个端点为M，直线l：3x－4y＝0交椭圆E于A，B两点．若|AF|＋|BF|＝4，点M 到直线l的距离不小于，则椭圆E的离心率的取值范围是(　A　)‎ A. B. C. D. 解析：设左焦点为F0，连接F‎0A，F0B，则四边形AFBF0为平行四边形．‎ ‎∵|AF|＋|BF|＝4，‎ ‎∴|AF|＋|AF0|＝4，∴a＝2.‎ 设M(0，b)，则M到直线l的距离d＝≥，∴1≤b<2.离心率e＝＝＝＝∈，故选A.‎