全国各地高考文科数学试题分类汇编立体几何专题含答案详解

全国各地高考文科数学试题分类汇编立体几何专题含答案详解

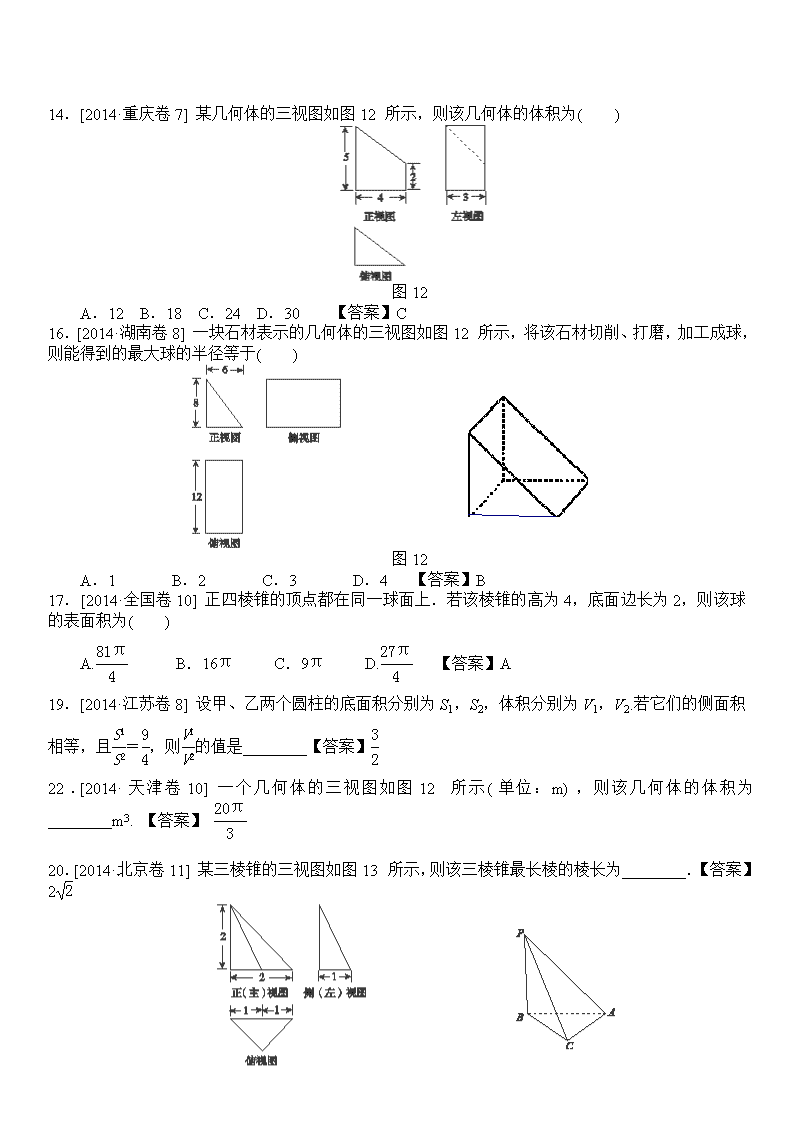
‎2014年全国各地高考文科数学试题分类汇编：立体几何 一、选择填空题 ‎1．[2014·福建卷3] 以边长为1的正方形的一边所在直线为旋转轴，将该正方形旋转一周所得圆柱的侧面积等于(　　)‎ A．2π B．π C．2 D．1 【答案】A　‎ ‎2．[2014·浙江卷3] 某几何体的三视图(单位：cm)如图所示，则该几何体的体积是(　　)‎ ‎ 图11‎ A．‎72 cm3 B．‎90 cm‎3 ‎ C．‎108 cm3 D．‎138 cm3 【答案】B　‎ ‎3．[2014·四川卷4] 某三棱锥的侧视图、俯视图如图11所示，则该三棱锥的体积是(锥体体积公式：V＝Sh，其中S为底面面积，h为高)(　　)‎ A．3 B．‎2 ‎‎ C. D．1【答案】D　‎ ‎4．[2014·辽宁卷4] 已知m，n表示两条不同直线，α表示平面．下列说法正确的是(　　)‎ A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊂α，则m⊥n C．若m⊥α，m⊥n，则n∥α D．若m∥α，m⊥n，则n⊥α 【答案】B　‎ ‎5．[2014·陕西卷5] 将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是(　　)‎ A．4π B．3π C．2π D．π 【答案】C　‎ ‎6．[2014·浙江卷6] 设m，n是两条不同的直线，α，β是两个不同的平面(　　)‎ A．若m⊥n，n∥α，则m⊥α B．若m∥β，β⊥α，则m⊥α C．若m⊥β，n⊥β，n⊥α，则m⊥α D．若m⊥n，n⊥β，β⊥α，则m⊥α【答案】C　‎ ‎7．[2014·全国卷4] 已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为(　　)‎ A. B. C. D. 【答案】B　‎ ‎8．[2014·新课标全国卷Ⅱ6] 如图11，网格纸上正方形小格的边长为1(表示‎1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为‎3 cm，高为‎6 cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为(　　)‎ 图11‎ A. B. C. D. 【答案】C　‎ ‎9．[2014·湖北卷10] ‎ ‎《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术“置如其周，令相乘也．又以高乘之，三十六成一．”该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式V≈L2h相当于将圆锥体积公式中的π近似取为(　　)‎ A. B. C. D. 【答案】B　‎ ‎10．[2014·新课标全国卷Ⅱ7] 正三棱柱ABC A1B‎1C1的底面边长为2，侧棱长为，D为BC中点，则三棱锥A B1DC1的体积为(　　)‎ A．3 B. C．1 D. 【答案】C　‎ ‎11．[2014·安徽卷8] 一个多面体的三视图如图12所示，则该多面体的体积是(　　)‎ 图12‎ A. B. C．6 D．7 【答案】A　‎ ‎13．[2014·辽宁卷7] 某几何体三视图如图12所示，则该几何体的体积为(　　)‎ 图12‎ A．8－ B．8－ C．8－π D．8－2π 【答案】C　‎ ‎14．[2014·重庆卷7] 某几何体的三视图如图12所示，则该几何体的体积为(　　)‎ 图12‎ A．12 B．‎18 C．24 D．30 【答案】C　‎ ‎16．[2014·湖南卷8] 一块石材表示的几何体的三视图如图12所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于(　　)‎ 图12‎ A．1 B．‎2 C．3 D．4 【答案】B　‎ ‎17．[2014·全国卷10] 正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为(　　)‎ A. B．16π C．9π D. 【答案】A　‎ ‎19．[2014·江苏卷8] 设甲、乙两个圆柱的底面积分别为S1，S2，体积分别为V1，V2.若它们的侧面积相等，且＝，则的值是________【答案】　‎ ‎22．[2014·天津卷10] 一个几何体的三视图如图12所示(单位：m)，则该几何体的体积为________m3. 【答案】 ‎20．[2014·北京卷11] 某三棱锥的三视图如图13所示，则该三棱锥最长棱的棱长为________．【答案】2 图13　‎ ‎21．[2014·山东卷13] 一个六棱锥的体积为2，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________．【答案】12‎ 三、解答题 ‎1． [2014·安徽卷19] 如图15所示，四棱锥P ABCD的底面是边长为8的正方形，四条侧棱长均为2.点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥‎ 平面GEFH.‎ 图15‎ ‎(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH的面积．‎ 解： (1)证明：因为BC∥平面GEFH，BC⊂平面PBC，且平面PBC∩平面GEFH＝GH，所以GH∥BC. 同理可证EF∥BC，因此GH∥EF.‎ ‎(2)连接AC，BD交于点O，BD交EF于点K，连接OP，GK.‎ 因为PA＝PC，O是AC的中点，所以PO⊥AC，同理可得PO⊥BD.又BD∩AC＝O，且AC，BD都在平面ABCD内，所以PO⊥平面ABCD.‎ 又因为平面GEFH⊥平面ABCD，且PO⊄平面GEFH，所以PO∥平面GEFH.‎ 因为平面PBD∩平面GEFH＝GK，所以PO∥GK，所以GK⊥平面ABCD.‎ 又EF⊂平面ABCD，所以GK⊥EF，所以GK是梯形GEFH的高．‎ 由AB＝8，EB＝2得EB∶AB＝KB∶DB＝1∶4，‎ 从而KB＝DB＝OB，即K是OB的中点．再由PO∥GK得GK＝PO，‎ 所以G是PB的中点，且GH＝BC＝4.由已知可得OB＝4，PO＝＝＝6，‎ 所以GK＝3，故四边形GEFH的面积S＝·GK＝×3＝18.‎ ‎2．[2014·重庆卷20] 如图14所示四棱锥PABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB＝2，∠BAD＝，M为BC上一点，且BM＝.‎ ‎(1)证明：BC⊥平面POM；(2)若MP⊥AP，求四棱锥PABMO的体积．‎ 图14‎ 解：(1)证明：如图所示，因为四边形ABCD为菱形，O为菱形的中心，连接OB，则AO⊥OB.因为∠BAD＝，所以OB＝AB·sin∠OAB＝2sin＝1.‎ 又因为BM＝，且∠OBM＝，在△OBM中，OM2＝OB2＋BM2－2OB·BM·cos∠OBM＝12＋－2×1××cos＝，所以OB2＝OM2＋BM2，故OM⊥BM.‎ 又PO⊥底面ABCD，所以PO⊥BC.从而BC与平面POM内的两条相交直线OM，PO都垂直，所以BC⊥平面POM.‎ ‎(2)由(1)可得，OA＝AB·cos∠OAB＝2×cos＝.‎ 设PO＝a，由PO⊥底面ABCD，知△POA为直角三角形，故PA2＝PO2＋OA2＝a2＋3.‎ 又△POM也是直角三角形，故PM2＝PO2＋OM2＝a2＋.连接AM，在△ABM中，AM2＝AB2＋BM2－2AB·BM·cos∠ABM＝22＋－2×2××cos＝.‎ 由已知MP⊥AP，故△APM为直角三角形，则PA2＋PM2＝AM2，即a2＋3＋a2＋＝，‎ 解得a＝或a＝－(舍去)，即PO＝.‎ 此时S四边形ABMO＝S△AOB＋S△OMB＝·AO·OB＋·BM·OM＝××1＋××＝.‎ 所以四棱锥PABMO的体积V四棱锥PABMO＝·S四边形ABMO·PO＝××＝.‎ ‎3．[2014·陕西卷17] 四面体ABCD及其三视图如图14所示，平行于棱AD，BC的平面分别交四面体的棱AB，BD，DC，CA于点E，F，G，H.‎ 图14‎ ‎(1)求四面体ABCD的体积；(2)证明：四边形EFGH是矩形．‎ 解：(1)由该四面体的三视图可知，BD⊥DC，BD⊥AD，AD⊥DC，BD＝DC＝2，AD＝1，‎ ‎∴AD⊥平面BDC，∴四面体ABCD的体积V＝××2×2×1＝.‎ ‎(2)证明：∵BC∥平面EFGH，平面EFGH∩平面BDC＝FG，平面EFGH∩ 平面ABC＝EH，‎ ‎∴BC∥FG，BC∥EH，∴FG∥EH. 同理EF∥AD，HG∥AD，∴EF∥HG，∴四边形EFGH是平行四边形．‎ 又∵AD⊥平面BDC，∴AD⊥BC，∴EF⊥FG，∴四边形EFGH是矩形．‎ ‎4．[2014·湖南卷18] 如图13所示，已知二面角αMNβ的大小为60°，菱形ABCD在面β内，A，B两点在棱MN上，∠BAD＝60°，E是AB的中点，DO⊥面α，垂足为O.‎ ‎ ‎ 图13‎ ‎(1)证明：AB⊥平面ODE；(2)求异面直线BC与OD所成角的余弦值．‎ 解：(1)证明：如图，因为DO⊥α，AB⊂α，所以DO⊥AB.‎ 连接BD，由题设知，△ABD 是正三角形，又E是AB的中点，所以DE⊥AB.而DO∩DE＝D，故AB⊥平面ODE.‎ ‎(2)因为BC∥AD，所以BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角．‎ 由(1)知，AB⊥平面ODE，所以AB⊥OE.又DE⊥AB，于是∠DEO是二面角αMNβ的平面角，从而∠DEO＝60°.‎ 不妨设AB＝2，则AD＝2，易知DE＝.在Rt△DOE中，DO＝DE·sin 60°＝.‎ 连接AO，在Rt△AOD中，cos∠ADO＝＝＝. 故异面直线BC与OD所成角的余弦值为.‎ ‎5．[2014·北京卷17] 如图15，在三棱柱ABC A1B‎1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A‎1C1，BC的中点．‎ ‎ ‎ 图15‎ ‎(1)求证：平面ABE⊥平面B1BCC1；(2)求证：C‎1F∥平面ABE；(3)求三棱锥E ABC的体积．‎ 解：(1)证明：在三棱柱ABC A1B‎1C1中，BB1⊥底面ABC，所以BB1⊥AB.‎ 又因为AB⊥BC，所以AB⊥平面B1BCC1，所以平面ABE⊥平面B1BCC1.‎ ‎(2)证明：取AB的中点G，连接EG，FG.‎ 因为E，F，G分别是A‎1C1，BC，AB的中点，所以FG∥AC，且FG＝AC，EC1＝A‎1C1.‎ 因为AC∥A‎1C1，且AC＝A‎1C1，所以FG∥EC1，且FG＝EC1，所以四边形FGEC1为平行四边形，所以C‎1F∥EG.‎ 又因为EG⊂平面ABE，C‎1F⊄平面ABE，所以C‎1F∥平面ABE.‎ ‎(3)因为AA1＝AC＝2，BC＝1，AB⊥BC，所以AB＝＝.‎ 所以三棱锥E ABC的体积V＝S△ABC·AA1＝×××1×2＝.‎ ‎7．[2014·江苏卷16] 如图14所示，在三棱锥P ABC中，D，E，F分别为棱PC，AC，AB的中点．已知PA⊥AC，PA＝6，BC＝8，DF＝5.‎ 求证：(1)直线PA∥平面DEF；(2)平面BDE⊥平面ABC.‎ 解：（1）∵为中点 ∴DE∥PA ‎∵平面DEF，DE平面DEF ∴PA∥平面DEF ‎（2）∵为中点 ∴ ∵为中点 ∴‎ ‎∴ ∴，∴DE⊥EF ‎∵，∴ ∵ ∴DE⊥平面ABC ‎∵DE平面BDE， ∴平面BDE⊥平面ABC．‎ ‎9．[2014·新课标全国卷Ⅱ18] 如图13，四棱锥P ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设AP＝1，AD＝，三棱锥P ABD的体积V＝，求A到平面PBC的距离．‎ ‎ ‎ 解：(1)证明：设BD与AC的交点为O，连接EO.‎ 因为ABCD为矩形，所以O为BD的中点．‎ 又E为PD的中点，所以EO∥PB，EO⊂平面AEC，PB⊄平面AEC，‎ 所以PB∥平面AEC.‎ ‎(2)V＝××PA×AB×AD＝AB，由V＝，可得AB＝.‎ 作AH⊥PB交PB于点H，由题设知BC⊥平面PAB，所以BC⊥AH，‎ 因为PB∩BC＝B，所以AH⊥平面PBC，又AH＝＝，‎ 所以点A到平面PBC的距离为.‎ ‎10．[2014·广东卷18] 如图12所示，四边形ABCD为矩形，PD⊥平面ABCD，AB＝1，BC＝PC＝2，作如图13折叠：折痕EF∥DC，其中点E，F分别在线段PD，PC上，沿EF折叠后点P叠在线段AD上的点记为M，并且MF⊥CF.‎ ‎(1)证明：CF⊥平面MDF；(2)求三棱锥M CDE的体积．‎ ‎　　　　 　图12　　　　　　　　图13‎ ‎11．[2014·山东卷18] 如图14所示，四棱锥PABCD中，AP⊥平面PCD，AD∥BC，AB＝BC＝AD，E，F分别为线段AD，PC的中点．‎ ‎ ‎ 图14‎ ‎(1)求证：AP∥平面BEF；(2)求证：BE⊥平面PAC.‎ 证明：(1)设AC∩BE＝O，连接OF，EC.由于E为AD的中点，‎ AB＝BC＝AD，AD∥BC，所以AE∥BC，AE＝AB＝BC，所以O为AC的中点．‎ 又在△PAC中，F为PC的中点，所以AP∥OF，又OF⊂平面BEF，AP⊄平面BEF，‎ 所以AP∥平面BEF.‎ ‎(2)由题意知，ED∥BC，ED＝BC，所以四边形BCDE为平行四边形，所以BE∥CD.‎ 又AP⊥平面PCD，所以AP⊥CD，所以AP⊥BE.‎ 因为四边形ABCE为菱形，所以BE⊥AC.‎ 又AP∩AC＝A，AP，AC⊂平面PAC，所以BE⊥平面PAC.‎ ‎12．[2014·江西卷19] 如图11所示，三棱柱ABC A1B‎1C1中，AA1⊥BC，A1B⊥BB1.‎ ‎(1)求证：A‎1C⊥CC1；‎ ‎(2)若AB＝2，AC＝，BC＝，问AA1为何值时，三棱柱ABC A1B‎1C1体积最大，并求此最大值．‎ ‎ ‎ 解：(1)证明：由AA1⊥BC知BB1⊥BC.又BB1⊥A1B，故BB1⊥平面BCA1，所以BB1⊥A‎1C.‎ 又BB1∥CC1，所以A‎1C⊥CC1.‎ ‎(2)方法一：设AA1＝x.在Rt△A1BB1中，A1B＝＝.‎ 同理，A‎1C＝＝.‎ 在△A1BC中，cos∠BA‎1C＝＝－，‎ sin∠BA‎1C＝，‎ 所以S△A1BC＝A1B·A‎1C·sin∠BA‎1C＝.‎ 从而三棱柱ABC A1B‎1C1的体积V＝S直·l＝S△A1BC·AA1＝.‎ 因为x＝＝，‎ 所以当x＝＝，即AA1＝时，体积V取到最大值.‎ ‎(2)方法二：过A1作BC的垂线，垂足为D，连接AD.‎ 由AA1⊥BC，A1D⊥BC，得BC⊥平面AA1D，故BC⊥AD.又∠BAC＝90°，‎ 所以S△ABC＝AD·BC＝AB·AC，得AD＝.‎ 设AA1＝x.在Rt△AA1D中，A1D＝＝，S△A1BC＝A1D·BC＝.‎ 从而三棱柱ABC A1B‎1C1的体积V＝S直·l＝S△A1BC·AA1＝.因为x＝＝，‎ 所以当x＝＝，即AA1＝时，体积V取到最大值.‎ ‎13．[2014·辽宁卷19] 如图14所示，△ABC和△BCD所在平面互相垂直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F，G分别为AC，DC，AD的中点．‎ ‎ ‎ ‎(1)求证：EF⊥平面BCG；(2)求三棱锥D BCG的体积．‎ ‎ 附：锥体的体积公式V＝Sh，其中S为底面面积，h为高．‎ 解：(1)证明：由已知得△ABC≌△DBC，因此AC＝DC.又G为AD的中点，所以CG⊥AD，‎ 同理BG⊥AD.又BG∩CG＝G，所以AD⊥平面BGC. 又EF∥AD，所以EF⊥平面BCG.‎ ‎(2)在平面ABC内，作AO⊥CB，交CB延长线于点O.‎ 由平面ABC⊥平面BCD，知AO⊥平面BDC.‎ 又G为AD的中点，所以G到平面BDC的距离h是AO长度的一半．‎ 在△AOB中，AO＝AB·sin 60°＝，‎ 所以V三棱锥D BCG＝V三棱锥G BCD＝·S△DBC·h＝×·BD·BC·sin 120°·＝.‎ ‎14．[2014·全国新课标卷Ⅰ19] 如图14，三棱柱ABC A1B‎1C1中，侧面BB‎1C1C为菱形，B‎1C的中点为O，且AO⊥平面BB‎1C1C.‎ ‎ ‎ ‎(1)证明：B‎1C⊥AB；(2)若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC A1B‎1C1的高．‎ 解：(1)证明：连接BC1，则O为B‎1C与BC1的交点．‎ 因为侧面BB‎1C1C为菱形，所以B‎1C⊥BC1. 又AO⊥平面BB‎1C1C，所以B‎1C⊥AO，‎ 由于BC1∩AO＝O，故B‎1C⊥平面ABO. 由于AB⊂平面ABO，故B‎1C⊥AB.‎ ‎(2)作OD⊥BC，垂足为D，连接AD.作OH⊥AD，垂足为H.‎ 由于BC⊥AO，BC⊥OD，且AO∩OD＝O，故BC⊥平面AOD，所以OH⊥BC.‎ 又OH⊥AD，且AD∩BC＝D，所以OH⊥平面ABC.‎ 因为∠CBB1＝60°，所以△CBB1为等边三角形，又BC＝1，可得OD＝.‎ 因为AC⊥AB1，所以OA＝B‎1C＝.‎ 由OH·AD＝OD·OA，且AD＝＝，得OH＝.‎ 又O为B‎1C的中点，所以点B1到平面ABC的距离为.故三棱柱ABC A1B‎1C1的高为.‎ ‎17．[2014·浙江卷20] 如图15，在四棱锥A BCDE中，平面ABC⊥平面BCDE，∠CDE＝∠BED＝90°，AB＝CD＝2，DE＝BE＝1，AC＝.‎ ‎ ‎ ‎(1)证明：AC⊥平面BCDE；(2)求直线AE与平面ABC所成的角的正切值．‎ 解：(1)证明：连接BD，在直角梯形BCDE中，由DE＝BE＝1，CD＝2，得BD＝BC＝，由AC＝，AB＝2，得AB2＝AC2＋BC2，即AC⊥BC.‎ 又平面ABC⊥平面BCDE，从而AC⊥平面BCDE.‎ ‎(2)在直角梯形BCDE中，由BD＝BC＝，DC＝2，得BD⊥BC.‎ 又平面ABC⊥平面BCDE，所以BD⊥平面ABC.‎ 作EF∥BD，与CB的延长线交于点F，连接AF，则EF⊥平面ABC.‎ 所以∠EAF是直线AE与平面ABC所成的角．‎ 在Rt△BEF中，由EB＝1，∠EBF＝，得EF＝，BF＝；‎ 在Rt△ACF中，由AC＝，CF＝，得AF＝.‎ 在Rt△AEF中，由EF＝，AF＝，得tan∠EAF＝.‎ 所以，直线AE与平面ABC所成的角的正切值是.‎ ‎18．[2014·重庆卷20] 如图14所示四棱锥PABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB＝2，∠BAD＝，M为BC上一点，且BM＝.‎ ‎(1)证明：BC⊥平面POM；(2)若MP⊥AP，求四棱锥PABMO的体积．‎ ‎ ‎ 解：(1)证明：如图所示，因为四边形ABCD为菱形，O为菱形的中心，‎ 连接OB，则AO⊥OB.因为∠BAD＝，所以OB＝AB·sin∠OAB＝2sin＝1.‎ 又因为BM＝，且∠OBM＝，‎ 在△OBM中，OM2＝OB2＋BM2－2OB·BM·‎ cos∠OBM＝12＋－2×1××cos＝，所以OB2＝OM2＋BM2，故OM⊥BM.‎ 又PO⊥底面ABCD，所以PO⊥BC.从而BC与平面POM内的两条相交直线OM，PO都垂直，所以BC⊥平面POM.‎ ‎(2)由(1)可得，OA＝AB·cos∠OAB＝2×cos＝.‎ 设PO＝a，由PO⊥底面ABCD，知△POA为直角三角形，故PA2＝PO2＋OA2＝a2＋3.‎ 又△POM也是直角三角形，故PM2＝PO2＋OM2＝a2＋.‎ 连接AM，在△ABM中，AM2＝AB2＋BM2－2AB·BM·‎ cos∠ABM＝22＋－2×2××cos＝.‎ 由已知MP⊥AP，故△APM为直角三角形，则PA2＋PM2＝AM2，即a2＋3＋a2＋＝，‎ 解得a＝或a＝－(舍去)，即PO＝.‎ 此时S四边形ABMO＝S△AOB＋S△OMB＝·AO·OB＋·BM·OM＝××1＋××＝.‎ 所以四棱锥PABMO的体积V四棱锥PABMO＝·S四边形ABMO·PO＝××＝.‎