- 2021-04-17 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届高三数学(文)二轮复习查漏补缺课时练习:(十) 第10讲 函数的图像
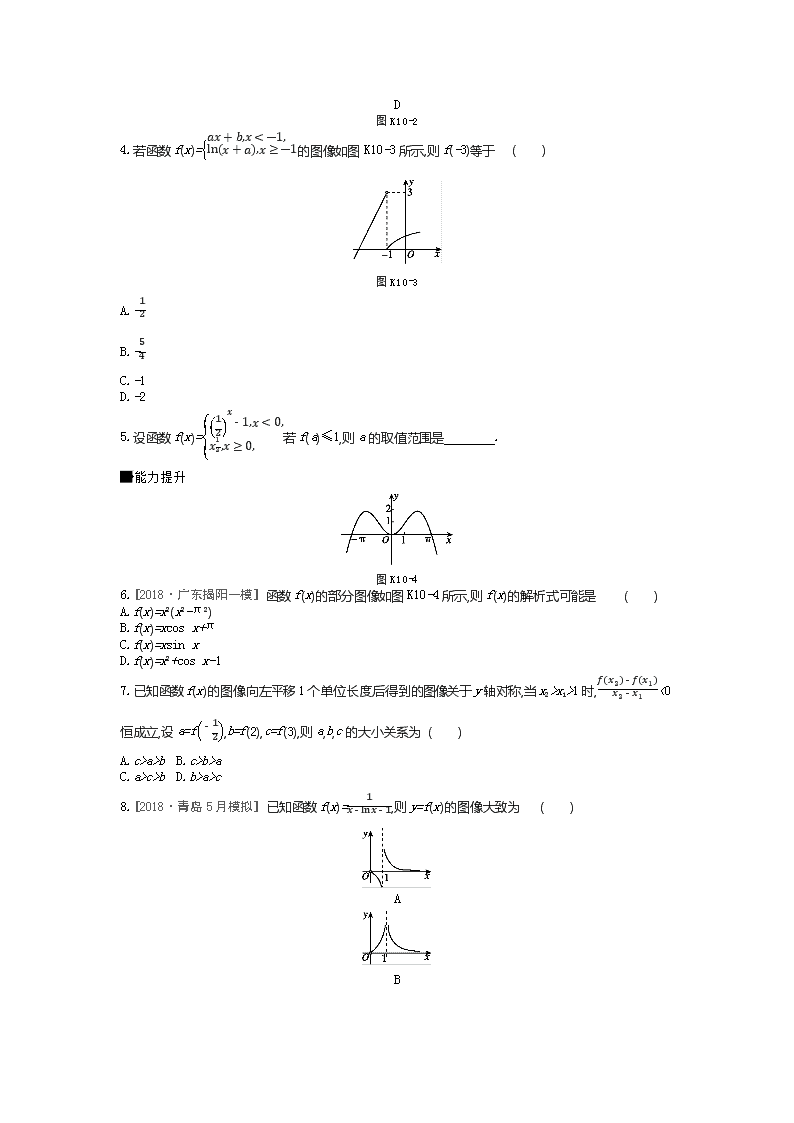
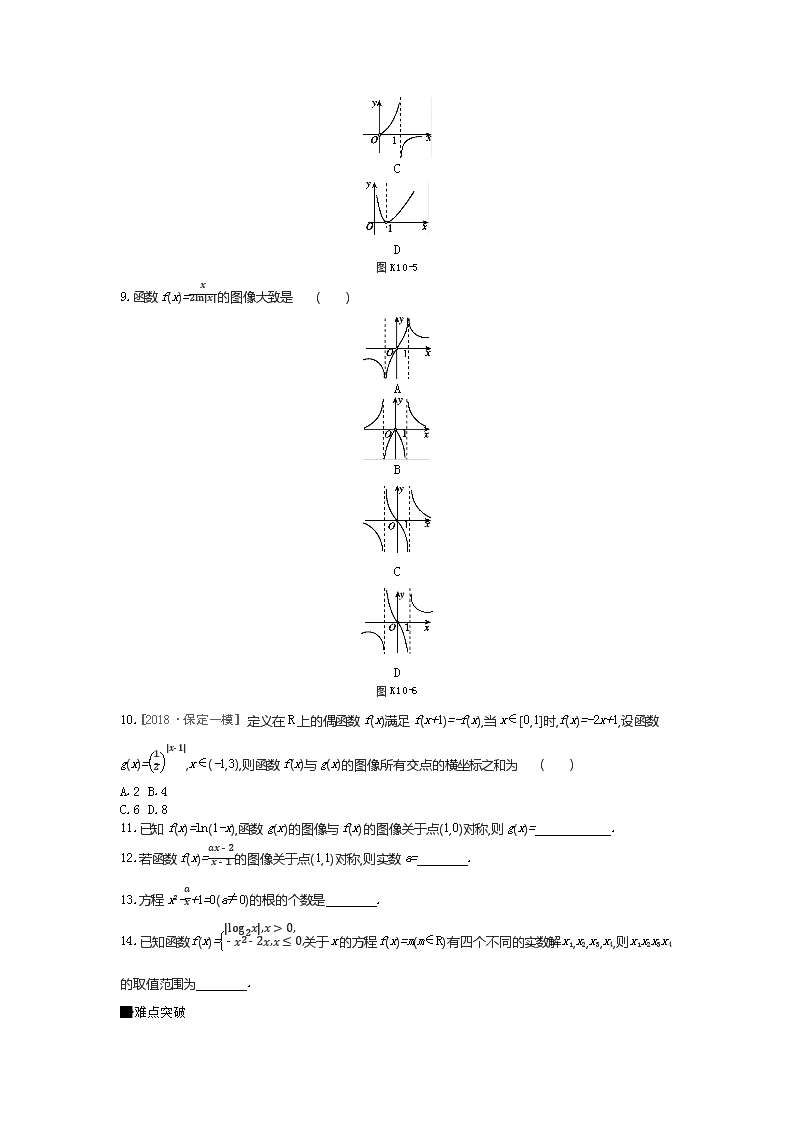
课时作业(十) 第10讲 函数的图像 时间 / 30分钟 分值 / 80分 基础热身 1.函数y=x|x|的图像大致是 ( ) A B C D 图K10-1 2.将函数f(x)=x2-2x的图像向右平移1个单位长度得到函数g(x)的图像,再将函数g(x)的图像向上平移2个单位长度得到函数h(x)的图像,则函数h(x)的最小值是 ( ) A.1 B.-2 C.2 D.-3 3.[2018·安徽皖江名校联考] 已知函数f(x)=ln|x|,g(x)=-x2+3,则y=f(x)·g(x)的图像为 ( ) A B C D 图K10-2 4.若函数f(x)=ax+b,x<-1,ln(x+a),x≥-1的图像如图K10-3所示,则f(-3)等于 ( ) 图K10-3 A.-12 B.-54 C.-1 D.-2 5.设函数f(x)=12x-1,x<0,x12,x≥0,若f(a)≤1,则a的取值范围是 . 能力提升 图K10-4 6.[2018·广东揭阳一模] 函数f(x)的部分图像如图K10-4所示,则f(x)的解析式可能是 ( ) A.f(x)=x2(x2-π2) B.f(x)=xcos x+π C.f(x)=xsin x D.f(x)=x2+cos x-1 7.已知函数f(x)的图像向左平移1个单位长度后得到的图像关于y轴对称,当x2>x1>1时,f(x2)-f(x1)x2-x1<0恒成立,设a=f-12,b=f(2),c=f(3),则a,b,c的大小关系为 ( ) A.c>a>b B.c>b>a C.a>c>b D.b>a>c 8.[2018·青岛5月模拟] 已知函数f(x)=1x-lnx-1,则y=f(x)的图像大致为 ( ) A B C D 图K10-5 9.函数f(x)=x2ln|x|的图像大致是 ( ) A B C D 图K10-6 10.[2018·保定一模] 定义在R上的偶函数f(x)满足f(x+1)=-f(x),当x∈[0,1]时,f(x)=-2x+1,设函数g(x)=12|x-1|,x∈(-1,3),则函数f(x)与g(x)的图像所有交点的横坐标之和为 ( ) A.2 B.4 C.6 D.8 11.已知f(x)=ln(1-x),函数g(x)的图像与f(x)的图像关于点(1,0)对称,则g(x)= . 12.若函数f(x)=ax-2x-1的图像关于点(1,1)对称,则实数a= . 13.方程x2-ax+1=0(a≠0)的根的个数是 . 14.已知函数f(x)=|log2x|,x>0,-x2-2x,x≤0,关于x的方程f(x)=m(m∈R)有四个不同的实数解x1,x2,x3,x4,则x1x2x3x4的取值范围为 . 难点突破 15.(5分)已知函数f(x)=-x2+2x,x≤0,ln(x+1),x>0,若|f(x)|≥ax,则a的取值范围是 ( ) A.(-∞,0] B.(-∞,1] C.[-2,1] D.[-2,0] 16.(5分)[2018·广东茂名3月联考] 已知函数f(x)=x2+x+2-x4-x,则 ( ) A.函数f(x)在区间[-1,3]上单调递增 B.函数f(x)在区间[-1,3]上单调递减 C.函数f(x)的图像关于直线x=1对称 D.函数f(x)的图像关于点(1,0)对称 课时作业(十) 1.D [解析] 显然y=x|x|是奇函数,排除A,B,C,故选D. 2.A [解析] 依题意,得f(x)=x2-2x=(x-1)2-1,g(x)=(x-2)2-1,h(x)=(x-2)2+1,所以函数h(x)的最小值是1.故选A. 3.C [解析] 由已知得y=f(x)·g(x)为偶函数,排除选项A,D,当x∈(0,1)时,f(x)<0,g(x)>0,y=f(x)·g(x)<0,排除B.故选C. 4.C [解析] 由图像可得a·(-1)+b=3,ln(-1+a)=0,得a=2,b=5,所以f(x)=2x+5,x<-1,ln(x+2),x≥-1,故f(-3)=2×(-3)+5=-1.故选C. 5.[-1,1] [解析] 在同一直角坐标系中,作出函数y=f(x)的图像和直线y=1,如图所示,它们相交于(-1,1)和(1,1)两点,由f(a)≤1,得-1≤a≤1. 6.C [解析] 当x∈(0,π)时,f(x)>0,排除选项A;由图知f(x)是偶函数,而f(x)=xcos x+π是非奇非偶函数,排除选项B;又f(π)=0,而选项D中f(π)>0,排除选项D.故选C. 7.D [解析] 因为函数f(x)的图像向左平移1个单位长度后得到的图像关于y轴对称,所以f(x)的图像关于直线x=1对称,所以a=f-12=f52,又f(x)在(1,+∞)上单调递减,所以f(2)>f52>f(3),即b>a>c.故选D. 8.B [解析] 由f1e=11e+1-1=e>0,排除选项A;由f(e)=1e-2>0排除选项C;又f(e2)=1e2-3>0,e2-3>e-2,所以f(e)>f(e2),排除选项D.故选B. 9.D [解析] 函数f(x)是奇函数,排除选项B.当0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档