- 2021-04-17 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2017届湖北省武汉二中高三下学期周练(3
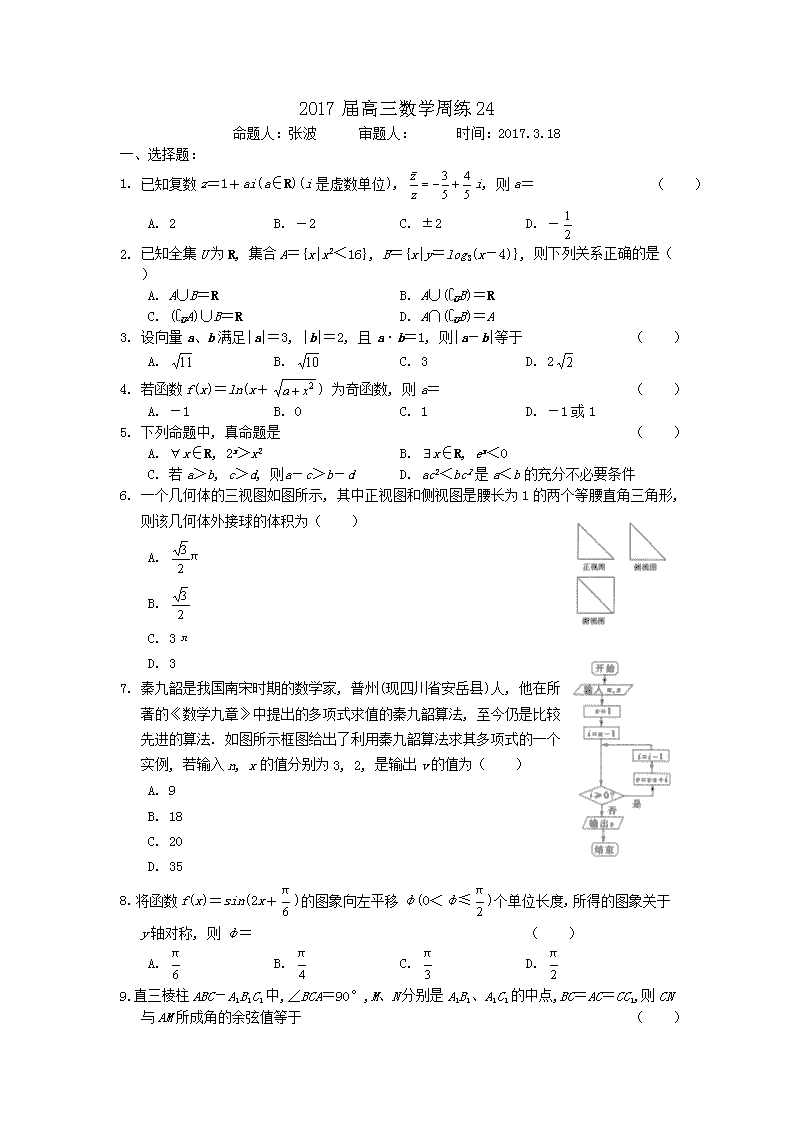
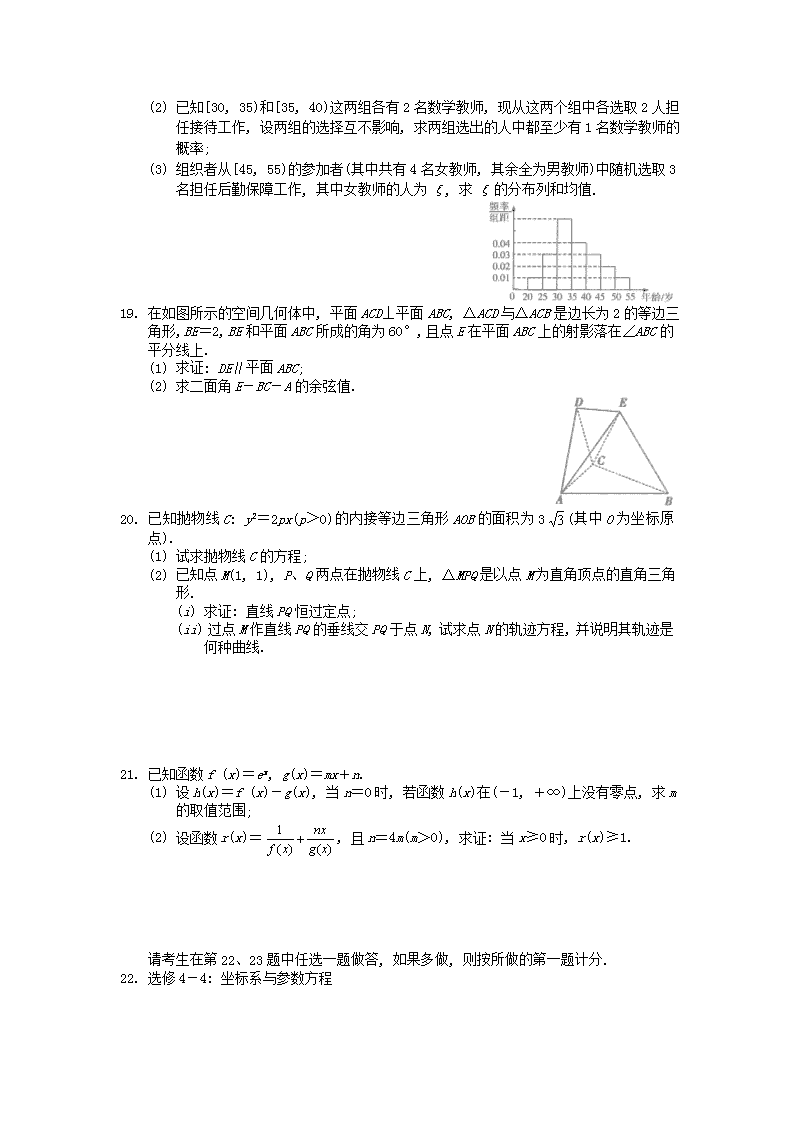
2017届高三数学周练24 命题人:张波 审题人: 时间:2017.3.18 一、选择题: 1. 已知复数z=1+ai(a∈R)(i是虚数单位), i, 则a= ( ) A. 2 B. -2 C. ±2 D. - 2. 已知全集U为R, 集合A={x|x2<16}, B={x|y=log3(x-4)}, 则下列关系正确的是( ) A. A∪B=R B. A∪(UB)=R C. (UA)∪B=R D. A∩(UB)=A 3. 设向量a、b满足|a|=3, |b|=2, 且a·b=1, 则|a-b|等于 ( ) A. B. C. 3 D. 2 4. 若函数f(x)=ln(x+) 为奇函数, 则a= ( ) A. -1 B. 0 C. 1 D. -1或1 5. 下列命题中, 真命题是 ( ) A. x∈R, 2x>x2 B. x∈R, ex<0 C. 若a>b, c>d, 则 a-c>b-d D. ac2<bc2是a<b的充分不必要条件 6. 一个几何体的三视图如图所示, 其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( ) A. B. C. 3π D. 3 7. 秦九韶是我国南宋时期的数学家, 普州(现四川省安岳县)人, 他在所著的《数学九章》中提出的多项式求值的秦九韶算法, 至今仍是比较先进的算法. 如图所示框图给出了利用秦九韶算法求其多项式的一个实例, 若输入n, x的值分别为3, 2, 是输出v的值为( ) A. 9 B. 18 C. 20 D. 35 8. 将函数f(x)=sin(2x+)的图象向左平移φ(0<φ≤)个单位长度, 所得的图象关于y轴对称, 则φ= ( ) A. B. C. D. 9. 直三棱柱ABC-A1B1C1中, ∠BCA=90°, M、N分别是A1B1、A1C1的中点, BC=AC=CC1,则CN与AM所成角的余弦值等于 ( ) A. B. C. D. 10. 某企业的4名职工参加职业技能考核, 每名职工均可从4个备选考核项目中任意抽取一个参加考核, 则恰有一个项目未被抽中的概率为 ( ) A. B. C. D. 11. 设F1, F2分别是椭圆C: (a>b>0)的左、右焦点, P为直线x=上一点, △F2PF1是底角为30°的等腰三角形, 则椭圆C的离心率为 ( ) A. B. C. D. 12. 对于函数f(x)=eax-1n x (a是实数), 下列结论正确的是 ( ) A. a=1时, f(x)有极大值, 且极大值点x0∈(, 1) B. a=2时, f(x)有极小值, 且极小值点x0∈(0, ) C. a=时, f(x)有极小值, 且极小值点x0∈(1, 2) D. a<0时, f(x)有极大值, 且极大值点x0∈(-∞, 0) 二、填空题: 13. 双曲线x2-2y2=1的渐近线方程为 . 14. 已知实数x, y满足则x2+y2的取值范围是 . 15. 若(x-2)5=a5x5+a4x4+a3x3+a2x2+a1x+a0, 则a1+a2+a3+a5= . (用数字作答) 16. 在△ABC中, sin(C-A)=1, sinB=, 则sinA= . 三、解答题 17. 在数列{an}中, a1=3, an=2an-1+(n-2)(n≥2, n∈N*). (1) 证明: 数列{an+n}是等比数列, 并求{an}的通项公式; (2) 求数列{an}的前n项和Sn. 18. 某中学利用周末组织教职员工进行了一次秋季登山健身的活动, 有N人参加, 现将所有参加者按年龄情况分为[20, 25), [25, 30), [30, 35), [35, 40), [40, 45), [45, 50), [50, 55)共七组, 其频率分布直方图如图所示, 已知[35, 40)这组的参加者是8人. (1) 求N和[30, 35)这组的参加者人数N1; (2) 已知[30, 35)和[35, 40)这两组各有2名数学教师, 现从这两个组中各选取2人担任接待工作, 设两组的选择互不影响, 求两组选出的人中都至少有1名数学教师的概率; (3) 组织者从[45, 55)的参加者(其中共有4名女教师, 其余全为男教师)中随机选取3名担任后勤保障工作, 其中女教师的人为ξ, 求ξ的分布列和均值. 19. 在如图所示的空间几何体中, 平面ACD⊥平面ABC, △ACD与△ACB是边长为2的等边三角形, BE=2, BE和平面ABC所成的角为60°, 且点E在平面ABC上的射影落在∠ABC的平分线上. (1) 求证: DE∥平面ABC; (2) 求二面角E-BC-A的余弦值. 20. 已知抛物线C: y2=2px(p>0)的内接等边三角形AOB的面积为3(其中O为坐标原点). (1) 试求抛物线C的方程; (2) 已知点M(1, 1), P、Q两点在抛物线C上, △MPQ是以点M为直角顶点的直角三角形. (i) 求证: 直线PQ恒过定点; (ii) 过点M作直线PQ的垂线交PQ于点N, 试求点N的轨迹方程, 并说明其轨迹是何种曲线. 21. 已知函数f (x)=ex, g(x)=mx+n. (1) 设h(x)=f (x)-g(x), 当n=0时, 若函数h(x)在(-1, +∞)上没有零点, 求m的取值范围; (2) 设函数r(x)=, 且n=4m(m>0), 求证: 当x≥0时, r(x)≥1. 请考生在第22、23题中任选一题做答, 如果多做, 则按所做的第一题计分. 22. 选修4-4: 坐标系与参数方程 已知直线l的参数方程为(t为参数), 在直角坐标系xOy中, 以O为极点, x轴正半轴为极轴建立极坐标系, 曲线M的方程为ρ2(1+sin2θ)=1. (1) 求曲线M的直角坐标方程; (2) 若直线l与曲线M只有一个公共点, 求倾斜角α的值. 23. 选修4-5: 不等式选讲 设a, b, c∈R+且a+b+c=1. (1) 求证: 2ab+bc+ca+≤; (2) 求证: ≥2. 2017届高三数学周练24参考答案 15. 41 22. 23.查看更多