【同步作业】人教版 八年级下册数学19函数的图象

【同步作业】人教版 八年级下册数学19函数的图象

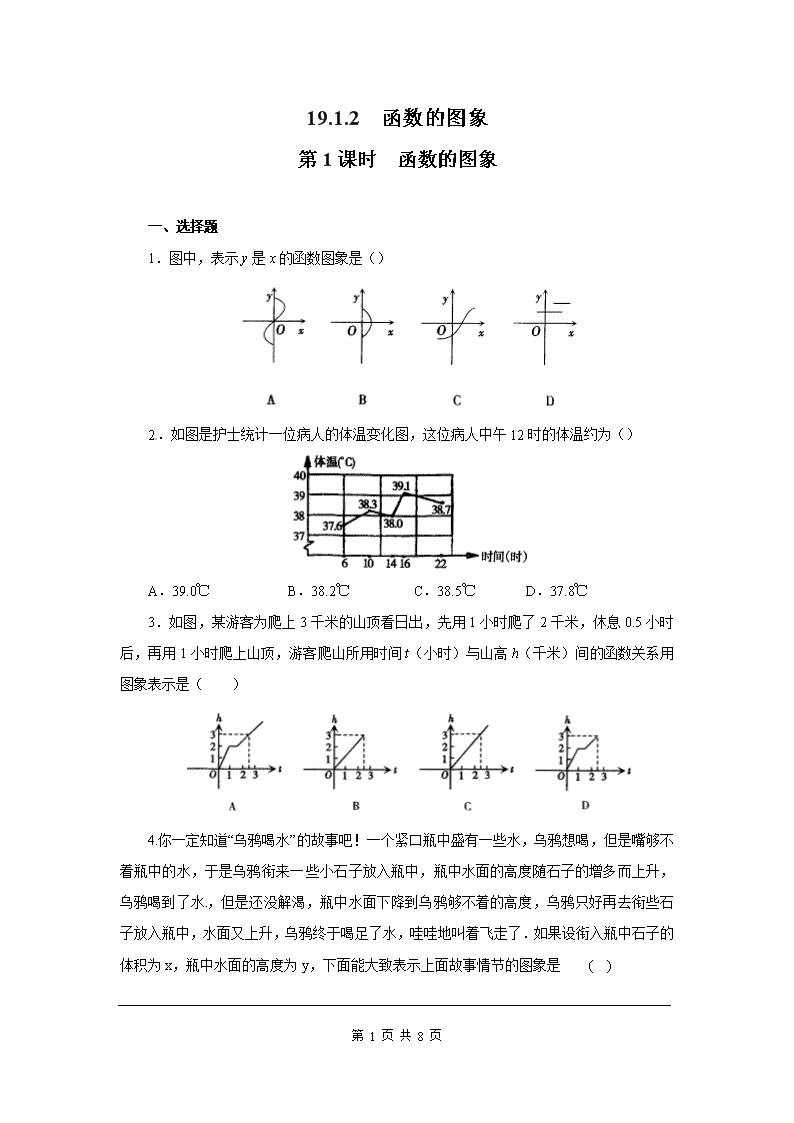
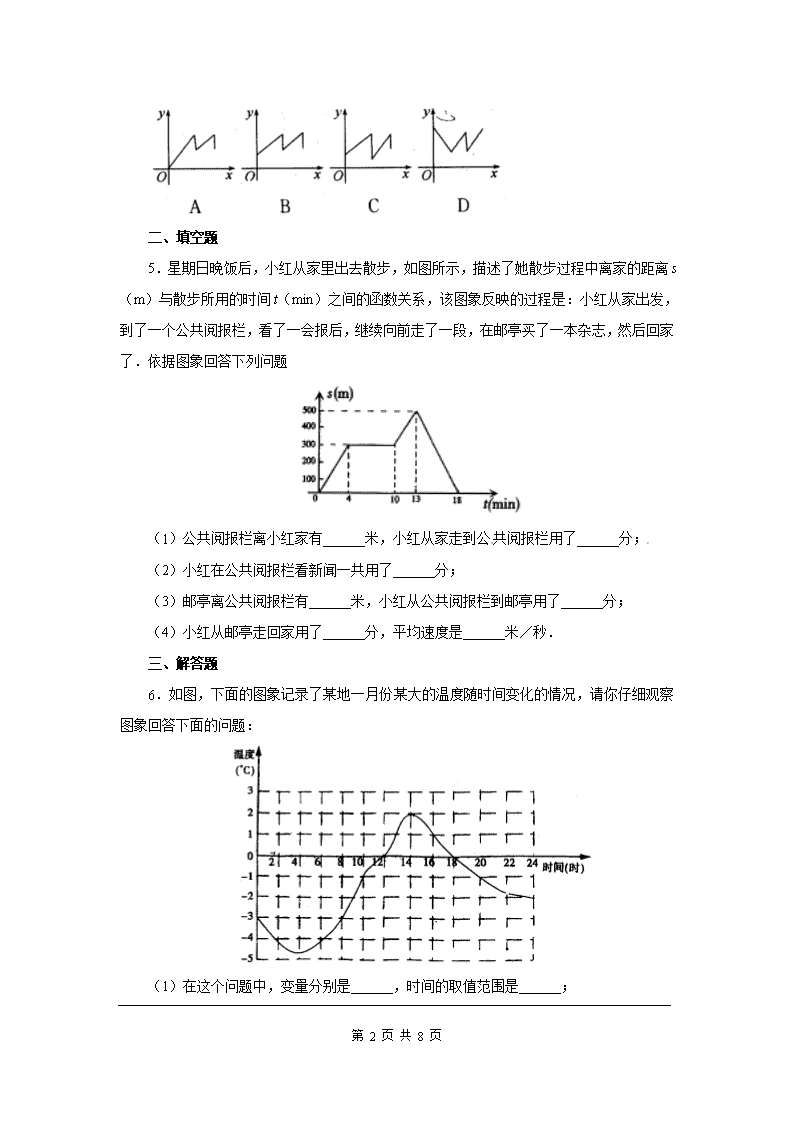
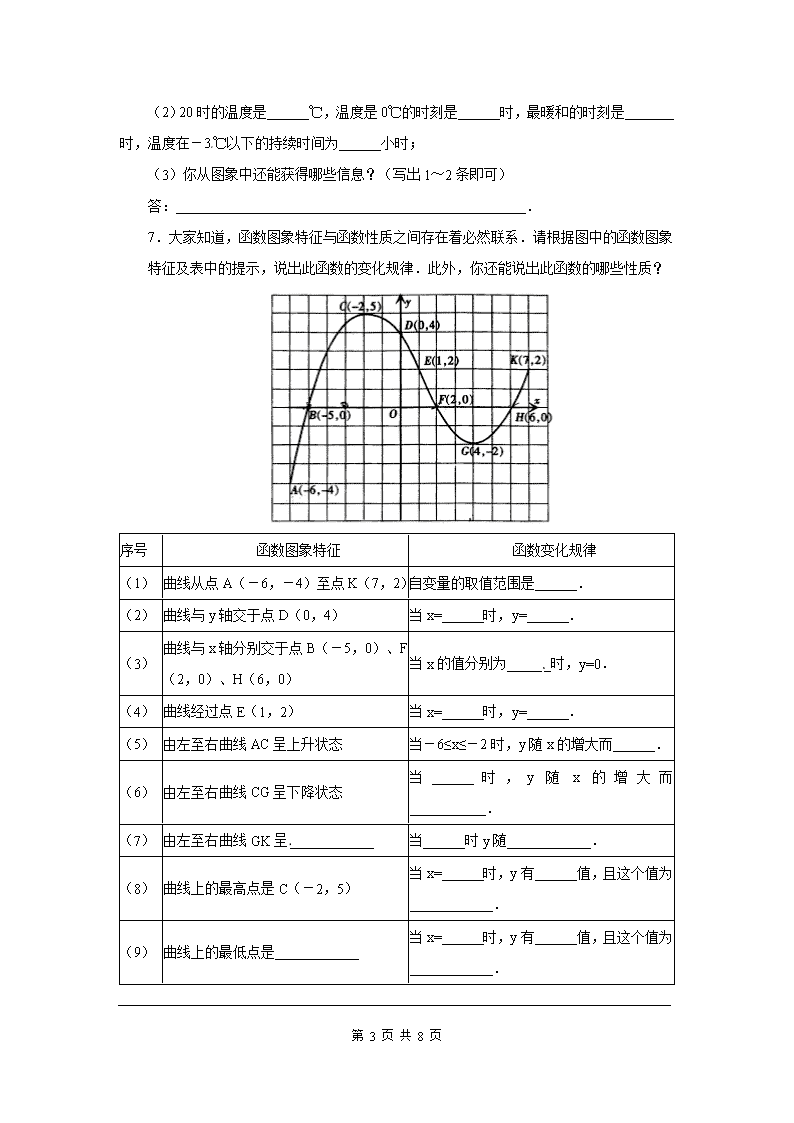
第 1 页 共 8 页 19.1.2 函数的图象 第 1 课时 函数的图象 一、选择题 1．图中，表示 y 是 x 的函数图象是（） 2．如图是护士统计一位病人的体温变化图，这位病人中午 12 时的体温约为（） A．39.0℃ B．38.2℃ C．38.5℃ D．37.8℃[来源:Z&xx&k.Com] 3．如图，某游客为爬上 3 千米的山顶看日出，先用 1 小时爬了 2 千米，休息 0.5 小时 后，再用 1 小时爬上山顶，游客爬山所用时间 t（小时）与山高 h（千米）间的函数关系用 图象表示是（ ） 4.你一定知道“乌鸦喝水”的故事吧！一个紧口瓶中盛有一些水，乌鸦想喝，但是嘴够不 着瓶中的水，于是乌鸦衔来一 些小石子放入瓶中，瓶中水面的高度随石子的增多而上升， 乌鸦喝到了水 ，但是还没解渴，瓶中水面下降到乌鸦够不着的高度，乌鸦只好再去衔些石 子放入瓶中，水面又上升，乌鸦终于喝足了水，哇哇地叫着飞走了．如果设衔入瓶中石子的 体积为 x，瓶中水面的高度为 y，下面能大致表示上面故事情节的图象是 ( ) 第 2 页 共 8 页 二、填空题 5．星期日晚饭后，小红从家里出去散步，如图所示，描述了她散步过程中离家的距离 s（m）与散步所用的时间 t（min）之间的函数关系，该图象反映的过程是：小红从家出发， 到了一个公共阅报栏，看了一会报后，继续向前走了一段，在邮亭买了一本杂志，然后回家 了．依据图象回答下列问题 （1）公共阅报栏离小红家有______米，小红从家走到公共阅报栏用了______分； （2）小红在公共阅报栏看新闻一共用了______分； （3）邮亭离公共阅报栏有______米，小红从公共阅报栏到邮亭用了______分； （4）小红从邮亭走回家用了______分，平均速度是______米／秒． 三、解答题 6．如图，下面的图象记录了某地一月份某大的温度随时间变化的情况，请你仔细观察 图象回答下面的问题： （1）在这个问题中，变量分别是______，时间的取值范围是______； 第 3 页 共 8 页 （2）20 时的温度是______℃，温度是 0℃的时刻是______时，最暖和的时刻是_______ 时，温度在－3℃以下的持续时间为______小时； （3）你从图象中还能获得哪些信息？（写出 1～2 条即可） 答：__________________________________________________． 7．大家知道，函数图象特征与函数性质之间存在着必然联系．请根据图中的函数图象 特征及表中的提示，说出此函数的变化规律．此外，你还能说出此函数的哪些性质？ 序号 函数图象特征 函数变化规律 （1） 曲线从点 A（－6，－4）至点 K（7，2）自变量的取值范围是______． （2） 曲线与 y 轴交于点 D（0，4） 当 x=______时，y=______． （3） 曲线与 x 轴分别交于点 B（－5，0）、F （2，0）、H（6，0） 当 x 的值分别为______时，y=0． （4） 曲线经过点 E（1，2） 当 x=______时，y=______． （5） 由左至右曲线 AC 呈上升状态 当－6≤x≤－2 时，y 随 x 的增大而______． （6） 由左至右曲线 CG 呈下降状态 当______时，y 随 x 的增大而___________． （7） 由左至右曲线 GK 呈____________ 当______时 y 随____________． （8） 曲线上的最高点是 C（－2，5） 当 x=______时，y 有______值，且这个值为 ____________． （9） 曲线上的最低点是____________ 当 x=______时，y 有______值，且这个值为 ____________． （10）曲线 BCF 位于 x 轴的上方 当______时，y______0． 第 4 页 共 8 页 8.（广州育才中学模拟）甲车速度为 20 米/秒，乙车速度为 25 米/秒。现甲车在乙车前 面 500 米，设 x 秒后两车之间的距离为 y 米。求 y 随 x（0≤x≤100）变化的函数解析式，并 画出函数图象。 9.（南京师大附中月考）一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而 行，两车在途中相遇后停留一段时间，然后分别按原速一同驶往甲地后停车。设慢车行驶的 时间为 x 小时，两车之间的距离为 y 千米，图中折线表示 y 与 x 之间的函数图象，请根据图 象解决下列问题： （1）甲、乙两地之间的距离为________千米； （2）求快车和慢车的速度。 10.某校办工厂现在的年产值是 15 万元，计划从今年开始，以后每年的年产值增加 2 万 元． (1)写出年产值 y（万元）与所经过的年数 x（年）（x 为整数）之间的函数关系式； (2)画出函数图象； (3)求 10 年后的年产值． 11.（南京模拟）看图说故事． 请你编写一个故事，使故事情境中出现的一对变量 x、y 满足图所示的函数关系，要求： (1)指出变量 x 和 y 的含义； (2)利用图中的数据说明这对变量变化过程的实际意义，其中需涉及“速度”这个量． 第 5 页 共 8 页 12.（长春模拟）在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下 a,b 两个情境： 情境 a：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学 校； 情境 b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进． (1)情境 a，b 所对应的函数图象分别是____，____（填写序号）； (2)请你为剩下的函数图象写出一个适合的情境.[来源:学.科.网 Z.X.X.K] 第 6 页 共 8 页 参考答案 1.C. 2.B. 3.D. 4.B 5.（1）300，4； （2）6； （3）200，3； （4）5． 6.（1）时间、温度， 0 24t  ； （2）-1,12 和 18,14,8； （3）12 时-18 时之间，温度都高于 0℃；答案不唯一。 7.（1） 6 7x   （2）0,4 （3）-5,2,6 （4）1,2 （5）增大 （6）－2≤x≤4，减小 （7）上升状态，4≤x≤7，x 的增大而增大 （8）-2，最大，5 （9）（-6，-4），-6，最小，-4 （10） 5 2x ＜ ＜ ，＞ 8. 分析：两车之间的距离等于已有距离减去两车的速度差乘以时间. 解：由题意可知，x秒后两车行驶路程分别是： 甲车为 20x 米，乙车为 25x 米，[来源:学,科,网] 两车行驶路程为 25x-20x=5x（米）， 两车之间距离为（500-5x）米， 所以 y 随 x 变化的函数解析式为 y=500-5x，0≤x≤100. 第 7 页 共 8 页 列表： x … 10 20 30 40 y … 450 400 350 300 x 50 60 70 80 … y 250 200 150 100 … 9.分析：（1）甲、乙两地之间的距离为未出发时两车之间的距离；（2）抓住两点：①是 相同而行，所行路程和=所行时间×速度和；②是快车行完全程用了 8-1=7（小时）. 解：（1）根据 x，y 的实际意义以及图像可知，甲、乙两地之间的距离是 560 千米. （2）由图象可知，两车 4 小时相遇，相遇后停留了 1 小时，然后快车行驶 3 小时到达 价低（点 D 表示快车到达甲地的时刻，此时慢车仍在返回的途中行驶）. ∴快车的速度=560÷7=80（千米/时）， 慢车的速度=（560-80×4）÷4=60（千米/时）. 点拨：与行程有关的图象信息题中如果要求速度，一定要从图中读到一定的时间内路程 的变化，用路程的变化除以时间的变化即为速度.相遇、追及问题中路程、速度、时间之间 的关系要注意. 10.解：(1)函数关系式为 y=15+2x(x≥0 且 x 为整数)． (2)列表如下： x 0 1 2 3 4 5 6 y=15+2x 15 17 19 21 23 25 27 函数图象如图． 第 8 页 共 8 页 (3)当 x=10 时，y=15+2×10=35. 答：10 年后的年产值是 35 万元. 11.解：本题答案不唯一，下列解法供参考． (1)该函数图象表示小明骑车离出发地的距离 y(单位：km)与他所用的时间 x(单位：min) 的关系． (2)小明以 0.4 km/min 的速度匀速骑了 5 min，原地休息了 6 min 后，以 0.5 km/min 的速 度匀速骑车回出发地． 12.解:(1)(3) (1) (2)情境是小芳离开家不久，休息了一会儿，又返回了家．