- 2021-04-17 发布 |
- 37.5 KB |
- 17页


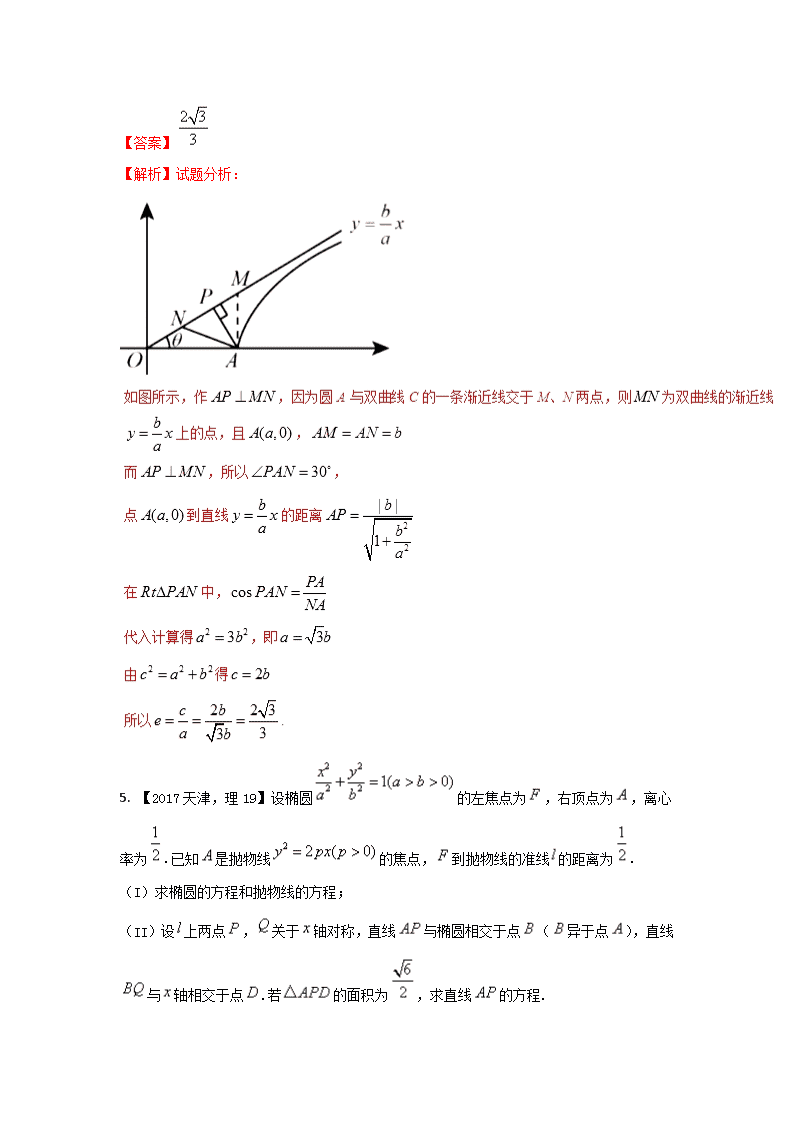
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题2-10 椭圆、双曲线、抛物线的几何性质的应用(练)-2018年高考数学(理)二轮复习讲练测
2018高三二轮复习之讲练测之练案【新课标版理科数学】 专题10 椭圆、双曲线、抛物线的几何性质的应用 1.练高考 1.【2017课标1,理10】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为 A.16 B.14 C.12 D.10 【答案】A 2.【2017课标II,理9】若双曲线(,)的一条渐近线被圆所截得的弦长为2,则的离心率为( ) A.2 B. C. D. 【答案】A 【解析】 3.【2017课标II,理16】已知是抛物线的焦点,是上一点,的延长线交轴于点。若为的中点,则 。 【答案】6 【解析】如图所示,不妨设点M位于第一象限,设抛物线的准线与轴交于点,做与点,与点, 4. 【2017课标1,理】已知双曲线C:(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________. 【答案】 【解析】试题分析: 5. 【2017天津,理19】设椭圆的左焦点为,右顶点为,离心率为.已知是抛物线的焦点,到抛物线的准线的距离为. (I)求椭圆的方程和抛物线的方程; (II)设上两点,关于轴对称,直线与椭圆相交于点(异于点),直线与轴相交于点.若的面积为,求直线的方程. 【答案】 (1), .(2),或. 【解析】 (Ⅱ)解:设直线的方程为,与直线的方程联立,可得点,故.将与联立,消去,整理得,解得,或.由点异于点,可得点.由,可得直线的方程为,令,解得,故.所以.又因为的面积为,故,整理得,解得,所以. 所以,直线的方程为,或. 6. 【2017山东,理21】在平面直角坐标系中,椭圆:的离心率为,焦距为. (Ⅰ)求椭圆的方程; (Ⅱ)如图,动直线:交椭圆于两点,是椭圆上一点,直线的斜率为,且,是线段延长线上一点,且,的半径为,是的两条切线,切点分别为.求的最大值,并求取得最大值时直线的斜率. 【答案】(I). (Ⅱ)的最大值为,取得最大值时直线的斜率为. (Ⅱ)设,联立方程 得,由题意知,且, 所以 . 由题意可知圆的半径为 由题设知,所以因此直线的方程为. 联立方程得,因此 . 2.练模拟 1.【2018届辽宁省沈阳市郊联体高三上学期期末】已知抛物线的焦点为,过点的直线交抛物线于两点,交准线于点,若,则( ) A. B. C. 3 D. 5 【答案】B 【解析】得p=2,作AM、BN垂直准线于点M、N,则|BN|=|BF|,又|BC|=2|BF|,得|BC|=2|BN|,∴ 故选B 2.等腰直角△内接于抛物线,为抛物线的顶点,,△ 的面积是16,抛物线的焦点为,若是抛物线上的动点,则的最大值为( ) A. B. C. D. 【答案】C 【解析】 因为等腰直角△内接于抛物线,为抛物线的顶点, 所以,可设,得,将代入,得,抛物线的方程为,所以,设,则,设,则 ,时,“” 成立.故选C. 3.【2018届黑龙江省牡丹江市第一高级中学高三上学期期末】如图,已知抛物线的方程为,过点A(0,﹣1)作直线与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为﹣3,则∠MBN的大小等于__________ 【答案】 4.【2018届河北省唐山市高三上学期期末】已知为抛物线: 的焦点,过点作两条互相垂直的直线,直线交于不同的两点,直线交于不同的两点,记直线的斜率为. (1)求的取值范围; (2)设线段的中点分别为点,求证: 为钝角. 【答案】(1){k|-<k<0或k>2}(2)见解析 【解析】试题分析: (1)由题意可设直线m的方程为y=k(x-2),将其代入抛物线方程后可得到一二次方程,根据判别式大于零可得k<0,或k>2.同理设直线n的方程为y=t(x-2),可得t<0,或t>2.根据以kt=-1,可解得k>0或-<k<0,从而可得所求范围.(2)由(1)可得点M(2k,2k2-2k),N(2t,2t2-2t),根据F(0,1)可得到的坐标,通过证明 且不共线可得为钝角. 试题解析: (1)由题可知k≠0,设直线m的方程为y=k(x-2), 由消去y整理得x2-4kx+8k=0,① 因为直线直线m交于不同的两点, 所以Δ=16k2-32k>0, 解得k<0,或k>2. 设直线n的方程为y=t(x-2), 由消去y整理得x2-4tx+8t=0, 同理由Δ>0可得t<0,或t>2. 因为m⊥n, 所以kt=-1, 得-,或-, 解得k>0或-<k<0. 故k的取值范围为{k|-<k<0或k>2}. (Ⅱ)设A(x1,y1),B(x2,y2),M(x0,y0). 由①得x1+x2=4k, 所以, 故, 所以点M(2k,2k2-2k). 同理可得N(2t,2t2-2t), 又F(0,1), 所以=(2k,2k2-2k-1), =(2t,2t2-2t-1), =4kt+(2k2-2k-1)(2t2-2t-1), 将kt=-1代入上式可得, =-2k2-2t2+6(k+t)-3=-2(k+t)2+6(k+t)-7=-2(k+t-)2-<0 因为2k(2t2-2t-1)-2t(2k2-2k-1)=2(+k)≠0, 所以与不共线. 所以可得∠MFN为钝角. 5.【2018届湖南省常德市高三上学期期末】}已知圆的一条直角是椭圆的长轴,动直线,当过椭圆上一点且与圆相交于点时,弦的最小值为. (1)求圆即椭圆的方程; (2)若直线是椭圆的一条切线, 是切线上两个点,其横坐标分别为,那么以为直径的圆是否经过轴上的定点?如果存在,求出定点坐标;若不存在,请说明理由. 【答案】(1).(2)过定点与. 【解析】试题分析:(1)先根据垂径定理求半径,再根据点在椭圆上解得, (2)设点的坐标,化简条件,再联立切线方程与椭圆方程,根据判别式为零得等量关系,代入并化简可得,即得结论 (2)联立方程,得到,由与椭圆相切,得到,① 易知,设以为直径的圆经过,设则有, 而,② 由①②可知, , 要使上式成立,有只有当,故经过定点与. 3.练原创 1. 在平面直角坐标系xOy中,已知椭圆C1:+=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上. (1)求椭圆C1的方程; (2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程. 【答案】(1)+y2=1.(2)y=x+或y=-x-. 【解析】(1)因为椭圆C1的左焦点为F1(-1,0),所以c=1. 将点P(0,1)代入椭圆方程+=1,得=1,即b=1,所以a2=b2+c2=2. 所以椭圆C1的方程为+y2=1. (2)直线l的斜率显然存在且不为0,设直线l的方程为y=kx+m, 由消去y并整理得: (1+2k2)x2+4kmx+2m2-2=0, 因为直线l与椭圆C1相切,所以Δ1=16k2m2-4(1+2k2)(2m2-2)=0, 整理得2k2-m2+1=0.① 由消去y并整理得: k2x2+(2km-4)x+m2=0. 因为直线l与抛物线C2相切, 所以Δ2=(2km-4)2-4k2m2=0, 整理得km=1.② 综合①②,解得或 所以直线l的方程为 y=x+或y=-x-. 2.如图, 等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上. (1)求抛物线E的方程. (2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q.证明:以PQ为直径的圆恒过y轴上某定点. 【答案】(1)x2=4y.(2)证明:见解析. 【解析】(1)依题意,|OB|=8,∠BOy=30°. 设B(x,y),则x=|OB|sin 30°=4, y=|OB|cos 30°=12. 因为点B(4,12)在x2=2py上, 所以(4)2=2p×12,解得p=2. 故抛物线E的方程为x2=4y. (2)证明:证法一 由(1)知y=x2,y′=x. 设P(x0,y0),则x0≠0,y0=x,且l的方程为 y-y0=x0(x-x0),即y=x0x-x. 由得 所以Q为. 设M(0,y1),令·=0对满足y0=x(x0≠0)的x0,y0恒成立. 由于=(x0,y0-y1),=, 由·=0, 得-y0-y0y1+y1+y=0, 即(y+y1-2)+(1-y1)y0=0.① 由于①式对满足y0=x(x0≠0)的y0恒成立, 所以解得y1=1. 故以PQ为直径的圆恒过y轴上的定点M(0,1). 证法二 由(1)知y=x2,y′=x,设P(x0,y0),则x0≠0,y0=x,且l的方程为y-y0=x0(x-x0),即y=x0x-x. 由得 所以Q为. 取x0=2,此时P(2,1),Q(0,-1),以PQ为直径的圆为(x-1)2+y2=2,交y轴于点M1(0,1),M2(0,-1);取x0=1,此时P,Q,以PQ为直径的圆为+=,交y轴于点M3(0,1),M4. 故若满足条件的点M存在,只能是M(0,1). 以下证明点M(0,1)就是所要求的点. 因为=(x0, y0-1),=,所以·=-2y0+2=2y0-2-2y0+2=0. 故以PQ为直径的圆恒过y轴上的定点M(0,1). 3. 已知椭圆C:+=1(a>b>0)的一个顶点为A (2,0),离心率为, 直线y=k(x-1)与椭圆C交于不同的两点M,N. (1)求椭圆C的方程. (2)当△AMN的面积为时,求k的值. 【答案】(1)+=1.(2)k=±1. 【解析】(1)由题意得解得b=. 所以椭圆C的方程为+=1. (2)由 得(1+2k2)x2-4k2x+2k2-4=0. 设点M,N的坐标分别为(x1,y1),(x2,y2), 则y1=k(x1-1),y2=k(x2-1), x1+x2=,x1x2=. 所以|MN|= = =. 又因为点A(2,0)到直线y=k(x-1)的距离d= . 所以△AMN的面积为 S=|MN|·d=. 由=,解得k=±1. 4.在平角坐标系中,椭圆的离心率,且过点,椭圆的长轴的两端点为,,点为椭圆上异于,的动点,定直线与直线,分别交于,两点. (1)求椭圆的方程; (2)在轴上是否存在定点经过以为直径的圆,若存在,求定点坐标;若不存在,说明理由. 【答案】(1);(2),. 【解析】 (1),∴椭圆的方程为; 设,的斜率分别为,,,则,, ,由:知,由:知,∴的中点, ∴以为直径的圆的方程为, 令,∴, ∴,∴, 即,解得或,∴存在定点,经过以为直径的圆. 查看更多