2017-2018学年江西省奉新县第一中学高二下学期期末考试数学（文）试题（Word版）

2017-2018学年江西省奉新县第一中学高二下学期期末考试数学（文）试题（Word版）

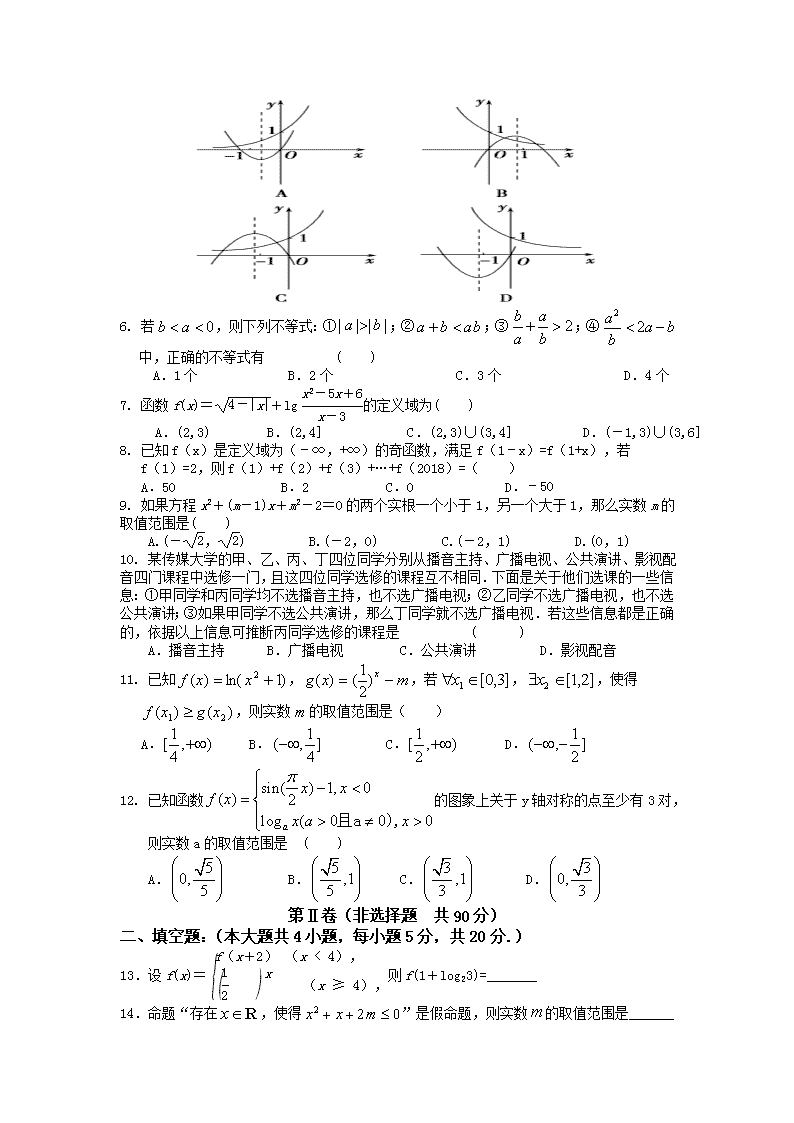
‎2017-2018学年江西省奉新县第一中学高二下学期期末考试数学（文）试卷 ‎(考试时间:120分钟 总分:150分)‎ ‎★祝考试顺利★‎ ‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共22题。考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试结束后，只交答题卡。‎ 注意事项：‎ ‎1、答题前，考生务必先将自己的姓名，学号填涂在答题卡上，并认真核对。‎ ‎2、各题答案均使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整，笔迹清楚。‎ ‎3、请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。‎ ‎4、保持卷面清洁，不折叠，不破损。‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ ‎1．已知集合A＝{x|x2＋x－2<0},B＝,则A∩B＝(　　)‎ ‎ A.{x|－1≤x<1} B.{－1,0,1} C.{－1,0} D.{0,1}‎ ‎2．已知是虚数单位，则复数的实部和虚部分别为 ( )‎ A．， B．， C．， D．，‎ ‎3．某社区针对该区的老年人是否需要特殊照顾进行了一项分性别的抽样调查,根据男性老年人和女性老年人需要特殊照顾和不需要特殊照顾得出了一个2×2的列联表,并计算得出K2的观测值k＝4.350,则下列结论正确的是(　　)‎ A.有97.5%的把握认为“该社区的老年人是否需要特殊照顾与性别有关”‎ B.有95%的把握认为“该社区的老年人是否需要特殊照顾与性别有关”‎ C.该社区需要特殊照顾的老年人中有95%是男性 D.该社区每100名老年人中有5名需要特殊照顾 参考数据：‎ P(K2>k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.01‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎4. 程序框图如下：‎ 如果上述程序运行的结果为S＝132，那么判断框中应填入（ ）‎ ‎ A、 B、 C、 D、‎ ‎5. 指数函数y＝与二次函数y＝ax2＋2bx(a∈R，b∈R)在同一坐标系中的图象可能是( )‎ ‎6. 若，则下列不等式：①；②；③；④中，正确的不等式有 ( )‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎7. 函数f(x)＝＋lg的定义域为(　　)‎ ‎ A．(2,3) B．(2,4] C．(2,3)∪(3,4] D．(－1,3)∪(3,6]‎ ‎8. 已知f（x）是定义域为（﹣∞，+∞）的奇函数，满足f（1﹣x）=f（1+x），若 f（1）=2，则f（1）+f（2）+f（3）+…+f（2018）=（　　）‎ ‎ A．50 B．‎2 ‎C．0 D．﹣50‎ ‎9. 如果方程x2＋(m－1)x＋m2－2＝0的两个实根一个小于1，另一个大于1，那么实数m的取值范围是(　　)‎ ‎ A.(－，) B.(－2，0) C.(－2，1) D.(0，1)‎ ‎10. 某传媒大学的甲、乙、丙、丁四位同学分别从播音主持、广播电视、公共演讲、影视配 音四门课程中选修一门，且这四位同学选修的课程互不相同．下面是关于他们选课的一些信 息：①甲同学和丙同学均不选播音主持，也不选广播电视；②乙同学不选广播电视，也不选 公共演讲；③如果甲同学不选公共演讲，那么丁同学就不选广播电视．若这些信息都是正确 的，依据以上信息可推断丙同学选修的课程是 ( )‎ ‎ A．播音主持 B．广播电视 C．公共演讲 D．影视配音 ‎11. 已知，，若，，使得 ‎，则实数的取值范围是（　　）‎ ‎ A． B． C． D．‎ ‎12. 已知函数的图象上关于y轴对称的点至少有3对， ‎ ‎ 则实数a的取值范围是 ( )‎ A． B． C． D．‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：（本大题共4小题，每小题5分，共20分.）‎ ‎13．设f(x)＝则f(1＋log23)= ‎ ‎14．命题“存在，使得”是假命题，则实数的取值范围是 ‎ ‎15. 直线 (t为参数)上与点P(－2，3)的距离等于的点的坐标是 ‎ ‎16. 设函数y=f（x）是定义在R上的奇函数，且满足f（x﹣2）=﹣f（x）对一切x∈R都成立，又当x∈[﹣1，1]时，f（x）=x3，则下列四个命题：‎ ‎①函数y=f（x）是以4为周期的周期函数；‎ ‎②当x∈[1，3]时，f（x）=（2﹣x）3； ‎ ‎③函数y=f（x）的图象关于x=1对称；‎ ‎④函数y=f（x）的图象关于（2，0）对称．‎ 其中正确的命题是　 ．‎ 三、解答题：(本大题共6小题，17题10分,18-22题12分,共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．（本小题满分10分）‎ ‎ 已知函数f(x)＝|2x＋1|，g(x)＝|x|＋a.‎ ‎ （Ⅰ）当a＝0时，解不等式f(x)≥g(x)；‎ ‎（Ⅱ）若存在x∈R，使得f(x)≤g(x)成立，求实数a的取值范围.‎ ‎18．（本小题满分12分）‎ ‎ 在直角坐标系中，圆的参数方程为，以为极点，轴的非负半轴为极轴建立极坐标系．‎ ‎ （Ⅰ）求圆的极坐标方程；‎ ‎ （Ⅱ）直线的极坐标方程是，射线与圆的交点为、，与直线的交点为，求线段的长．‎ ‎19．（本小题满分12分）‎ ‎ 已知幂函数在上单调递增，函数.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）当时，记，的值域分别为集合，设命题,命题，若命题是成立的必要条件，求实数的取值范围.‎ ‎20．（本小题满分12分）‎ 参加一中数学实践课的同学，对某公司的一种产品销量与价格进行了统计，得到如下数据和散点图：‎ 定价x（元/kg）‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 年销量y（kg）‎ ‎1150‎ ‎643‎ ‎424‎ ‎262‎ ‎165‎ ‎86‎ z=2lny ‎14.1‎ ‎12.9‎ ‎12.1‎ ‎11.1‎ ‎10.2‎ ‎8.9‎ ‎（参考数据： ，，）‎ ‎（Ⅰ）根据散点图判断，y与x，z与x哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？‎ ‎（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程（方程中的系数均保留两位有效数字）．‎ ‎ (III)定价为多少元/kg时，年利润的预报值最大？‎ 附：对于一组数据（x1，y1），（x2，y2），（x3，y3），…，（xn，yn），其回归直线=•x+的斜率和截距的最小二乘估计分别为：‎ ‎==，=﹣•．‎ ‎21.（本小题满分12分）‎ 1． 函数对一切实数x、y均有成立，且．‎ ‎ （Ⅰ）求的值；‎ ‎ （Ⅱ）当在上恒成立时，求实数a的取值范围．‎ ‎22.（本小题满分12分）‎ 已知是方程的两个不等实根，函数的定义域为。‎ ‎（Ⅰ）判断函数在定义域内的单调性，并证明。‎ ‎（Ⅱ）记：，若对任意，恒有成立，‎ 求实数a 的取值范围。‎ ‎2019届高二下学期期末考试数学（文）试卷答案 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ 题号 ‎1‎ ‎2 ‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C D B A C C C B C D A A 二、填空题：（本大题共4小题，每小题5分，共20分.）‎ ‎ 13. 14. 15. 16.①②③④ ‎ 三、解答题：(本大题共6小题，17题10分,18-22题12分,共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．（本小题满分10分）‎ ‎ 已知函数f(x)＝|2x＋1|，g(x)＝|x|＋a.‎ ‎ （Ⅰ）当a＝0时，解不等式f(x)≥g(x)；‎ ‎（Ⅱ）若存在x∈R，使得f(x)≤g(x)成立，求实数a的取值范围.‎ 解（Ⅰ）当a＝0时，由f(x)≥g(x)得|2x＋1|≥|x|，‎ 两边平方整理得3x2＋4x＋1≥0，………2分 解得x≤－1或x≥－.‎ ‎∴原不等式的解集为(－∞，－1]∪………5分 ‎（Ⅱ）由f(x)≤g(x)得a≥|2x＋1|－|x|，……6分 令h(x)＝|2x＋1|－|x|，‎ 即h(x)＝………8分 故h(x)min＝h＝－，‎ 所求实数a的取值范围为…………..10分 ‎18．（本小题满分12分）‎ ‎ 在直角坐标系中，圆的参数方程为，以为极点，轴的非负半轴为极轴建立极坐标系．‎ ‎ （Ⅰ）求圆的极坐标方程；‎ ‎ （Ⅱ）直线的极坐标方程是，射线与圆的交点为、，与直线的交点为，求线段的长．‎ 解：（Ⅰ）利用cos2φ+sin2φ=1，把圆C的参数方程为参数）化为（x﹣1）2+y2=1，∴ρ2﹣2ρcosθ=0，即ρ=2cosθ．………………4分 ‎（Ⅱ）设（ρ1，θ1）为点P的极坐标，由，解得．…….7分 设（ρ2，θ2）为点Q的极坐标，由，解得．……10分 ‎∵θ1=θ2，∴|PQ|=|ρ1﹣ρ2|=2．‎ ‎∴|PQ|=2．…………12分 ‎19．（本小题满分12分）‎ ‎ 已知幂函数在上单调递增，函数.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）当时，记，的值域分别为集合，设命题,命题，若命题是成立的必要条件，求实数的取值范围.‎ 解：（Ⅰ）依题意得：或 当时，在上单调递减，与题设矛盾，舍去 ‎． ……………4分 ‎（Ⅱ）当时，，单调递增，，…8分 由命题是成立的必要条件，得，． …12分 ‎20．（本小题满分12分）‎ 参加一中数学实践课的同学，对某公司的一种产品销量与价格进行了统计，得到如下数据和散点图：‎ 定价x（元/kg）‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 年销量y（kg）‎ ‎1150‎ ‎643‎ ‎424‎ ‎262‎ ‎165‎ ‎86‎ z=2lny ‎14.1‎ ‎12.9‎ ‎12.1‎ ‎11.1‎ ‎10.2‎ ‎8.9‎ ‎（参考数据：，，）‎ ‎（Ⅰ）根据散点图判断，y与x，z与x哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？‎ ‎（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程（方程中的系数均保留两位有效数字）．‎ ‎ (III)定价为多少元/kg时，年利润的预报值最大？‎ 附：对于一组数据（x1，y1），（x2，y2），（x3，y3），…，（xn，yn），其回归直线=•x+‎ 的斜率和截距的最小二乘估计分别为：‎ ‎==，=﹣•．‎ 解：（Ⅰ）由散点图可知：z与x具有较强的线性相关性；……3分 ‎（Ⅱ）由==35，==11.55，‎ ‎==≈﹣0.10，…5分 由=﹣•=15.05≈15，‎ ‎=x+=15﹣0.10x，……7分 线性回归方程为：=15﹣0.10x，则y关于x的回归方程==，‎ ‎∴y关于x的回归方程==；……9分 ‎(III)年利润L（x）=x•=x•，‎ 求导L′（x）=•（1﹣x•），‎ 令导L′（x）=0，解得：x=20，‎ 由函数的单调性可知：当x=20时，年利润的预报值最大，‎ ‎∴定价为20元/kg时，年利润的预报值最大．…………12分 ‎21.（本小题满分12分）‎ 1． 函数对一切实数x、y均有成立，且．‎ ‎ （Ⅰ）求的值；‎ ‎ （Ⅱ）当在上恒成立时，求实数a的取值范围．‎ 解：(1) 令y = 0，x = 1代入已知式子 得 ‎∵ ∴…….4分 ‎(2) 在 ‎∴ ………7分 由 ‎∵ 上是减函数 要恒成立，只需即可…….10分 即 ，∴ …..12分 ‎22.（本小题满分12分）‎ 已知是方程的两个不等实根，函数 的定义域为。‎ ‎（Ⅰ）判断函数在定义域内的单调性，并证明。‎ ‎（Ⅱ）记：，若对任意，恒有成立，‎ 求实数a 的取值范围。‎ 证一：设 ‎ 则 又 故在区间上是增函数。 …………….6分 ‎ 证二：‎ 易知：当 ‎ 故在区间上是增函数。 ‎ 二解：恒成立。‎ ‎…12分