2018届二轮复习客观题专题十不等式课件（15张)（全国通用）

2018届二轮复习客观题专题十不等式课件（15张)（全国通用）

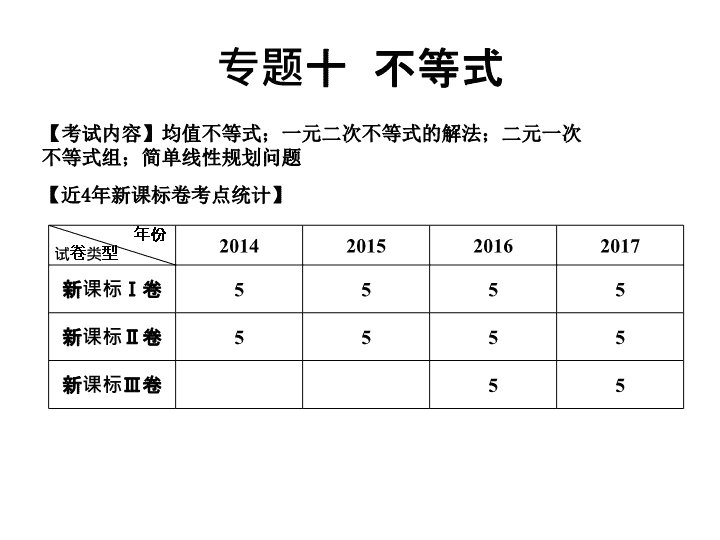
专题十 不等式 【近 4 年新课标卷考点统计 】 【 考试内容 】 均值不等式；一元二次不等式的解法；二元一次 不等式组；简单线性规划问题 年份 试卷类型 2014 2015 2016 2017 新课标Ⅰ卷 5 5 5 5 新课标Ⅱ卷 5 5 5 5 新课标 Ⅲ 卷 5 5 四、简单的线性规划 1.判断二元一次不等式 Ax + By + C >0在平面直角坐标系中表示 Ax + By + C =0某一侧所有点组成的平面区域.只需在直线某一侧取一个特殊点( x 0 , y 0 ),从 Ax 0 + By 0 + C 的正负即可判断 Ax + By + C >0表示直线哪一侧的平面区域 . 特别地,当 C ≠0时,通常把原点作为此特殊点. 一般地,我们把直线画成虚线以表示区域不包括边界直线 . 当我们在坐标系中画不等式 Ax + By + C ≥0所表示的平面区域时,此区域应包括边界直线,则把直线画成实线. 2 . 求线性规划问题的步骤是: (1)根据实际问题的约束条件列出不等式; (2)作出可行域,写出目标函数; (3)确定目标函数最优位置,从而获得最优解. 考点训练 【 解析 】 特殊值法，取 a =2 ， b =-1, 经验证 . 只有 C 成立，故选 C. 1 . 设 a , b ∈R,若 a -| b |>0,则下列不等式中正确的是 ( ) A. b-a >0 B. a 3 + b 3 <0 C. b + a >0 D. a 2 - b 2 <0 C 考点训练 2 . 设 a > b >1, c <0,给出下列三个结论: ① ; ② a c < b c ; ③log b ( a - c )>log a ( b - c ), 其中所有的正确结论的序号是 ( ) A.① B.①② C.②③ D.①②③ 【 解析 】 特殊值法 , 取 a =3, b =2, c =-1, 故选 D. D 考点训练 3 . 不等式 <0的解集是 ( ) A.(1,+∞) B.(-∞,-2) C.(-2,1) D.(-∞,-2)∪(1,+∞) 【 解析 】 原不等式等价于 ( x -1)( x +2)<0, 解得 -2< x <1, 故选 C. C 70 考点训练 B 考点训练 C 考点训练 【 解析 】 原不等式组所表示的平面区域如图中阴影部分所示 . 易知，当直线 x +2 y = z 过点 B 时，目标函数 z=x+2y 取最小值 . 易得点 B 的坐标为（ -1 ， -2 ） . 即： z min = － 1 ＋ 2×( － 2)= － 5, 故选 C. 14 . 满足约束条件| x |+2| y |≤2的目标函数 z = y - x 的最小值是 . 考点训练 -2 【 解析 】 原不等式所表示的平面区域如图中阴影部分所示 . 易知，当直线 y = x + z 过点 C 时，目标函数 z = y - x 取最小值 . 易得点 C 的坐标为（ 2 ， 0 ） 即： z min =-2. 考点训练 C 考点训练 详见 《 艺考生文化课冲刺点金 · 数 学 》 书中 P45-47 其他题